陕西省榆林市定边县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-06-10 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2^﹣3＝（）

A、 $- \frac{1}{8}$ B、 $\frac{1}{8}$ C、8 D、﹣8

查看试题解析
2. 下列交通标志图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，点 $O$ 在直线 $A B$ 上， $C O ⊥ A B$ ，若 $∠ C O D = 52 °$ ，则 $∠ A O D$ 的度数是（）

A、 $38 °$ B、 $128 °$ C、 $142 °$ D、 $150 °$

查看试题解析
4. 下列运算正确的是（）

A、 $m^{2} + m^{2} = m^{4}$ B、 $4 m^{2} n \div \frac{1}{2} m n = 8 m$ C、 ${(3 m n)}^{2} = 6 m^{2} n^{4}$ D、 ${(m + 2)}^{2} = m^{2} + 4$

查看试题解析
5. 下列事件中，是随机事件的是（）

A、抛出的篮球会下落 B、爸爸买彩票中奖了 C、地球绕着太阳转 D、一天有24小时

查看试题解析

6. 已知声音在空气中的传播速度与空气的温度有关，在一定范围内，其关系如下表所示：

温度/ $° C$	$- 20$	$- 10$	0	10	20	30
传播速度/ $m / s$	318	324	330	336	342	348

下列说法错误的是（）

A、自变量是温度，因变量是传播速度 B、温度越高，传播速度越快 C、当温度为

10 ° C

时，声音

5 s

可以传播

1650 m

D、温度每升高

10 ° C

，传播速度增加

6 m / s

查看试题解析

7. 如图， $A E // B D$ ， $∠ 1 = 115 °$ ， $∠ 2 = 40 °$ ，则 $∠ C$ 的度数是（）

A、 $15 °$ B、 $25 °$ C、 $35 °$ D、 $45 °$

查看试题解析
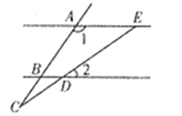8. 抛掷一枚质地均匀的骰子，六个面上分别标有数字1、2、3、4、5、6，则朝上一面的数字恰好为3的倍数的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{2}{3}$

查看试题解析
9. 如图，D、E分别是△ABC的边AC、BC上的点，且△ADB≌△EDB≌△EDC ，则∠C的度数为（）

A、15º B、20º C、25º D、30º

查看试题解析
10. 如图， $Δ A B P$ 与 $Δ C D P$ 是一对全等的等边三角形，且 $P A ⊥ P D$ ，下列四个结论：① $∠ P B C = 30 °$ ；② $A D // B C$ ；③ $P C ⊥ A B$ ；④四边形 $A B C D$ 是轴对称图形.其中正确的是（）

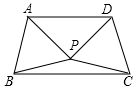A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

11. 某球形病毒颗粒直径约为0.0000001，将0.0000001用科学记数法表示为.

查看试题解析
12. 如图，把两根钢条 $A B$ ， $C D$ 的中点连在一起做成卡钳，可测量工件内槽的宽，已知 $A C$ 的长度是 $6 c m$ ，则工件内槽的宽 $B D$ 是cm．

查看试题解析
13. 若 $| y - 3 | + {(3 x - 2 y)}^{2} = 0$ ，则 ${(- y)}^{x} =$ .

查看试题解析
14. 如图，将一张长方形纸条折叠，若 $∠ A B C = 25 °$ ，则 $∠ A C D$ 的度数为.

查看试题解析

三、解答题

15. 计算： ${(\frac{1}{3})}^{- 1} + {(- 1)}^{2020} + 3^{5} \div 3^{2}$ .

查看试题解析
16. 如图，在△ABC中，AB＝AC，DE是线段AB的垂直平分线，△BCE的周长是18，BC＝8，求AB的长.

查看试题解析
17. 已知，如图，直线AB与直线BC相交于点B，点D是直线BC上一点
求作：点E，使直线DE∥AB，且点E到B、D两点的距离相等（在题目的原图中完成作图）

结论：BE=DE

查看试题解析
18. 如图，EF∥AD，∠1＝∠2，∠BAG＝60°，求∠G的度数.

查看试题解析
19. 先化简，再求值： $[(a b + 4) (a b - 4) - 5 a^{2} b^{2} + 16] \div a b$ ，其中 $a = 10$ ， $b = \frac{3}{4}$ .

查看试题解析
20.
已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB的平分线．
求证：AB=DC．

查看试题解析
21. 一个不透明的袋子里装有5个红球、3个黄球和4个蓝球，这些球除颜色外完全相同，从中随机摸出一个球，求：

(1)、摸出红球的概率；

(2)、摸出蓝球的概率；

(3)、摸出的不是红球的概率.

查看试题解析
22. 如图，在等腰△ABC中，∠A是顶角，N是边AB上任意一点（不与点A、B重合），过点N作NM⊥AB于点N，交BC的延长线于点M，若∠A＝30°，求∠NMB的度数.

查看试题解析
23. “龟兔赛跑”的故事同学们都非常熟悉，下图是乌龟、兔子赛跑过程中的路程 $s$ （米）与时间 $t$ （分钟）的关系，请根据图中给出的信息，回答下列问题.

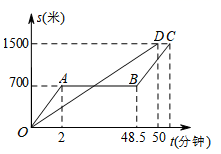(1)、赛跑的全路程是多少米？

(2)、兔子在赛跑过程中睡了几分钟？

(3)、兔子在睡觉前每分钟跑多少米？乌龟每分钟爬多少米？

查看试题解析
24. 如图，AB＝AD＝BC＝DC，∠C＝∠D＝∠ABE＝∠BAD＝90°，点E、F分别在边BC、CD上，∠EAF＝45°，过点A作∠GAB＝∠FAD，且点G在CB的延长线上.

(1)、△GAB与△FAD全等吗？为什么？

(2)、若DF＝2，BE＝3，求EF的长.

查看试题解析
25. 如图1，点A、B在直线l₁上，点C、D在直线l₂上，AE平分∠BAC，CE平分∠ACD.且∠EAC+∠ACE＝90°

(1)、判断直线l₁与l₂的位置关系，并说明理由；

(2)、如图2，P为线段AC上一定点，Q为直线l₂上一动点，当点Q在直线l₂上运动时（不与点C合），猜想∠CPQ、∠CQP与∠BAC之间的数量关系，并说明理由.

查看试题解析