湖北省咸宁市通山县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-06-10 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中,点P(1,-2)在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知 ${\begin{cases} \end{cases} \begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 是二元一次方程 $2 x + ay = 4$ 的一组解，则a的值为（）

A、2 B、 $- 2$ C、1 D、 $- 1$

查看试题解析
3. 面积为 2 的正方形的边长是（）

A、2的平方根 B、2的算术平方根 C、2开平方的结果 D、2的立方根

查看试题解析
4. 下列调查中，适宜采用全面调查的是（）

A、调查某批次汽车的抗撞击能力 B、企业招聘，对应聘人员进行面试 C、了解全国中学生的视力和用眼卫生情况 D、调查春节联欢晚会的收视率

查看试题解析
5. 如图，在下列条件中，不能判定AB∥DF的是（）

A、 $∠ A + ∠ A F D = 180 °$ B、 $∠ A = ∠ C F D$ C、 $∠ B E D = ∠ E D F$ D、 $∠ A = ∠ B E D$

查看试题解析
6. 如图，数轴上表示1， $\sqrt{2}$ 的对应点分别为A，B，点C在数轴上，且AC=AB，则点C表示的数是（）

A、 $\sqrt{2} - 1$ B、 $1 - \sqrt{2}$ C、 $2 - \sqrt{2}$ D、 $\sqrt{2} - 2$

查看试题解析
7. 经过直线 l 外一点O的四条直线中，与直线l相交的直线至少有（）

A、1条 B、2条 C、3条 D、4条

查看试题解析
8. 用三个不等式 $a > b$ ， $a b > 0$ ， $\frac{1}{a} < \frac{1}{b}$ 中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

9. 计算： $\sqrt[3]{- 8}$ = ．

查看试题解析
10. 如果点 $P (a - 1, a + 2)$ 在 $y$ 轴上，则 $a$ 的值为.

查看试题解析
11. 结合下图，用符号语言表达定理“同旁内角互补，两直线平行”的推理形式：∵ ， ∴a∥b.

查看试题解析
12. 不等式 $3 x - 5 \leq 2 (x - 1)$ 的正整数解的和为.

查看试题解析
13. 《九章算术》中记载：“今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而钱亦五十，问甲、乙持钱各几何？”译文：“假设有甲乙二人，不知其钱包里有多少钱，若乙把自己一半的钱给甲，则甲的钱数为50；而甲把自己 $\frac{2}{3}$ 的钱给乙，则乙的钱数也能为50．问甲、乙各有多少钱？”设甲持钱数为x，乙持钱数为y，可列方程组为．

查看试题解析
14. 如图，灯塔P位于小岛A北偏东38°方向，位于小岛B北偏西23°方向，则∠APB的度数为.

查看试题解析
15. 将正整数按如图的规律排列，若用有序数对（m，n）表示从上到下第m行，和该行从左到右第n个数，如（4，2）表示整数8，则（8，4）表示的整数是.

查看试题解析
16. 课外活动中，80名学生自由组合分成12组，各组人数分别有5人、7人和8人三种情况，设5人一组的有x组，7人一组的有y组，8人一组的有z组，有下列结论：
① ${\begin{array}{l} x + y + z = 12 \\ 5 x + 7 y + 8 z = 80 \end{array}$ ；② $x = \frac{1}{2} z + 2$ ；③ $y = - \frac{3}{2} z + 10$ ；④5人一组的最多有5组.

其中正确的有.（把正确结论的序号都填上）

查看试题解析

三、解答题

17. 完成下面的证明.
已知：如图，点A，B，C，D在一条直线上，CE与BF交于点G，∠A=∠1，CE∥DF，

求证：∠E=∠F.

证明：∵∠A=∠1，（已知），

∴AE∥BF，（），

∴∠E=∠2（），

∵CE∥DF，（已知），

∴∠F=∠2，（），

∴∠E=∠F.（）.

查看试题解析
18. 解下列方程组：

(1)、 ${\begin{array}{l} x - y = 4 \\ 4 x + 2 y = - 1 \end{array}$

(2)、 ${\begin{array}{l} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{array}$

查看试题解析
19. 解不等式组 ${\begin{array}{l} 2 x - 1 > x + 1 \\ 4 x - 1 \geq x + 8 \end{array}$ ，并把它的解集在数轴上表示出来.

查看试题解析
20. 随着科技的进步和网络资源的丰富，在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论.为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图.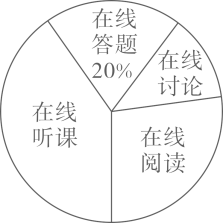

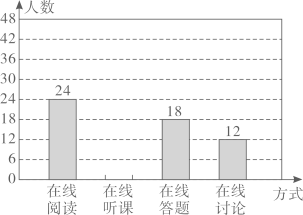
根据图中信息，解答下列问题：

(1)、求本次调查的学生总人数，并补全条形统计图；

(2)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

(3)、该校共有学生 $2100$ 人，请你估计该校对在线阅读最感兴趣的学生人数.

查看试题解析
21. 在正方形的网格中，按要求画出图形.

(1)、如图1，画出将三角形ABC先向右平移2个单位长度，再向上平移3个单位长度后得到的图形；

(2)、如图2，你能想办法在网格内通过构图测量出直线a，b所成的角的度数吗？请画出相应的图形，并测量出这两条直线所成的角的度数.

查看试题解析
22. 学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元.

(1)、求A，B两种奖品的单价；

(2)、学校准备购买A，B两种奖品共30个，且A奖品的数量不少于B奖品数量的 $\frac{1}{3}$ .请设计出最省钱的购买方案，并说明理由.

查看试题解析
23. 阅读材料：形如 $2 < 2 x + 1 < 3$ 的不等式，我们就称之为双连不等式.求解双连不等式的方法一，转化为不等式组求解，如 ${\begin{array}{l} 2 < 2 x + 1 \\ 2 x + 1 < 3 \end{array}$ ；方法二，利用不等式的性质直接求解，双连不等式的左、中、右同时减去1，得 $1 < 2 x < 2$ ，然后同时除以2，得 $\frac{1}{2} < x < 11$ .
解决下列问题：

(1)、请你写一个双连不等式并将它转化为不等式组；

(2)、利用不等式的性质解双连不等式 $2 \geq - 2 x + 3 > - 5$ ；

(3)、已知 $- 3 \leq x < - \frac{5}{2}$ ，求 $3 x + 5$ 的整数值.

查看试题解析
24. 如图，在平面直角坐标系中，点 $A (2 ， 6)$ ， $B (4 ， 3)$ ，将线段AB进行平移，使点A刚好落在x轴的负半轴上，点B刚好落在y轴的负半轴上，A，B的对应点分别为 $A^{'}$ ， $B^{'}$ ，连接 $A A^{'}$ 交y轴于点C， $B B^{'}$ 交x轴于点D.

(1)、线段 $A^{'} B^{'}$ 可以由线段AB经过怎样的平移得到？并写出 $A^{'}$ ， $B^{'}$ 的坐标；

(2)、求四边形 $A A^{'} B B^{'}$ 的面积；

(3)、P为y轴上的一动点（不与点C重合），请探究 $∠ P C A^{'}$ 与 $∠ A^{'} D B^{'}$ 的数量关系，给出结论并说明理由.

查看试题解析