湖北省武汉江区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2021-06-10 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、 B、 C、 D、2. 如图是一个不等式组的解集在数轴上的表示,则该不等式组的解集是( )
 A、 B、 C、 D、3. 下列调查,适合全面调查的是( )A、调查某批次汽车的抗撞能力 B、调查春节联欢晚会的收视率 C、鞋厂检测生产的鞋底能承受的弯折次数 D、了解某班学生的身高情况4. 下列各点中,在第二象限的是( )A、(﹣1,3) B、(1,﹣3) C、(﹣1,﹣3 ) D、(1,3)5. 如图,若 ,则可推出 ,其推理的根据是( )
A、 B、 C、 D、3. 下列调查,适合全面调查的是( )A、调查某批次汽车的抗撞能力 B、调查春节联欢晚会的收视率 C、鞋厂检测生产的鞋底能承受的弯折次数 D、了解某班学生的身高情况4. 下列各点中,在第二象限的是( )A、(﹣1,3) B、(1,﹣3) C、(﹣1,﹣3 ) D、(1,3)5. 如图,若 ,则可推出 ,其推理的根据是( ) A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、内错角相等,两直线平行6. 下列式子正确的是( )A、 B、 C、 D、7. 若 ,则下列式子正确的是( )A、 B、 C、 D、8. 张翔从学校出发骑自行车去县城,中途因道路施工步行了一段路, 后到达县城.他骑车的平均速度是 ,步行的平均速度是 ,路程全长 .他骑车与步行各走了多少千米?设他骑自行车行了 ,步行走了 ,则可列方程组为( )A、 B、 C、 D、9. 如图,已知点 为 内一点, , , 交 于点 ,若 ,则 的度数为( )
A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、内错角相等,两直线平行6. 下列式子正确的是( )A、 B、 C、 D、7. 若 ,则下列式子正确的是( )A、 B、 C、 D、8. 张翔从学校出发骑自行车去县城,中途因道路施工步行了一段路, 后到达县城.他骑车的平均速度是 ,步行的平均速度是 ,路程全长 .他骑车与步行各走了多少千米?设他骑自行车行了 ,步行走了 ,则可列方程组为( )A、 B、 C、 D、9. 如图,已知点 为 内一点, , , 交 于点 ,若 ,则 的度数为( ) A、 B、 C、 D、10. 若关于 的不等式组 无解,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 若关于 的不等式组 无解,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
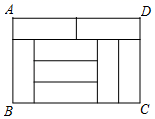
11. 已知 是方程 的一个解,则 的值为.12. 的小数部分为.13. 在画频数分布直方图时,一个样本容量为 的样本,最小值为 ,最大值为 .若确定组距为 ,则分成的组数是.14. 如图,由 个大小相同的小长方形无缝拼接成一个大长方形,已知大长方形的周长为 ,则小长方形的周长为 .
 15. 二元一次方程 中,若 的取值范围是 ,则 的最大值是.16. 已知关于 , , 的方程组 ,则 .17. 假期到了, 名女教师去外地培训,住宿时宾馆有足够多的 人间和 人间可供租住,但每个租住的房间都要按床位数住满,她们共有种租住方案.18. 关于 的不等式 的解集为 ,则关于 的不等式 的解集为.19. 如图,在平面直角坐标系中,有若干个横坐标和纵坐标分别为整数的点,其顺序按图中“ ”方向排列,第 个点为 ,后面依次为 , , , , ,根据这个规律,第 个点的坐标为.
15. 二元一次方程 中,若 的取值范围是 ,则 的最大值是.16. 已知关于 , , 的方程组 ,则 .17. 假期到了, 名女教师去外地培训,住宿时宾馆有足够多的 人间和 人间可供租住,但每个租住的房间都要按床位数住满,她们共有种租住方案.18. 关于 的不等式 的解集为 ,则关于 的不等式 的解集为.19. 如图,在平面直角坐标系中,有若干个横坐标和纵坐标分别为整数的点,其顺序按图中“ ”方向排列,第 个点为 ,后面依次为 , , , , ,根据这个规律,第 个点的坐标为.
三、解答题
-
20.(1)、计算: ;(2)、解方程组:21. 解不等式或不等式组,并将解集在数轴上表示出来.(1)、 ;(2)、22. 某校为了进一步丰富学生的课外阅读,准备购买一批课外书,为此对学校部分学生进行了“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):

请根据图中提供的信息,完成下列问题:
(1)、在这次问卷调查中,一共调查了名学生,并将上面的条形统计图补充完整;(2)、扇形统计图中 , “体育”所对的圆心角的度数为度;(3)、如果全校共有学生 人,请通过计算估计该校最喜欢“文学”类的学生比最喜欢“天文”类的学生多多少人.23. 已知,如图,在三角形 中, 平分 交 于点 , , 分别在 , 的延长线上, , . (1)、求证: ;(2)、若 , 比 大 ,求 的度数24. 如图所示,在平面直角坐标系中, 的三个顶点 , , 的坐标分别是 , , ;点 是 内部的一点,平移 ,点 随 一起平移,点 , , , 的对应点的分别是 , , , .若点 坐标为 .
(1)、求证: ;(2)、若 , 比 大 ,求 的度数24. 如图所示,在平面直角坐标系中, 的三个顶点 , , 的坐标分别是 , , ;点 是 内部的一点,平移 ,点 随 一起平移,点 , , , 的对应点的分别是 , , , .若点 坐标为 .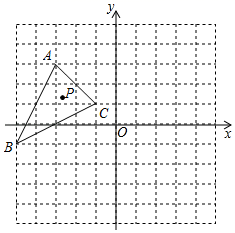 (1)、画出平移后的 ;(2)、连接 , ,已知 交 轴于点 ,则四边形 的面积为;点 的坐标为;(3)、已知 交 轴于点 ,若 恰好在线段 上,且满足 ,则此时 的坐标为(说明: 表示三角形 的面积,后面类似)25. 用白铁皮做罐头盒,每张铁皮可制盒身 个,或制盒底 个,一个盒身与两个盒底配成一套罐头盒,现有 张白铁皮.(1)、问用多少张制盒身、多少张制盒底可以使盒身与盒底正好配套;(2)、已知一张白铁皮的成本为 元,每张制作盒底的加工费为 元 张,而制作盒身的加工方式有横切和纵切两种,横切的加工费为 元 张,纵切的加工费为 元 张,受工艺限制,白铁皮横切的张数不超过纵切的 ,问在(1)结论下,应安排多少张横切多少张纵切才能使总费用最少,此时最少费用是多少.26. 已知,关于 的不等式组 有解.(1)、若上不等式的解集与 的解集相同,求 的值;(2)、若上不等式有 个整数解
(1)、画出平移后的 ;(2)、连接 , ,已知 交 轴于点 ,则四边形 的面积为;点 的坐标为;(3)、已知 交 轴于点 ,若 恰好在线段 上,且满足 ,则此时 的坐标为(说明: 表示三角形 的面积,后面类似)25. 用白铁皮做罐头盒,每张铁皮可制盒身 个,或制盒底 个,一个盒身与两个盒底配成一套罐头盒,现有 张白铁皮.(1)、问用多少张制盒身、多少张制盒底可以使盒身与盒底正好配套;(2)、已知一张白铁皮的成本为 元,每张制作盒底的加工费为 元 张,而制作盒身的加工方式有横切和纵切两种,横切的加工费为 元 张,纵切的加工费为 元 张,受工艺限制,白铁皮横切的张数不超过纵切的 ,问在(1)结论下,应安排多少张横切多少张纵切才能使总费用最少,此时最少费用是多少.26. 已知,关于 的不等式组 有解.(1)、若上不等式的解集与 的解集相同,求 的值;(2)、若上不等式有 个整数解①若 ,求 的取值范围;
②若 ,则 的取值范围为 ▲ .
27. 已知,在平面直角坐标系中, 为坐标原点,点 的坐标为 ,点 的坐标为 ,其中 , 满足 .
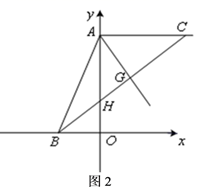 (1)、求点 、点 的坐标;(2)、将 点向右平移 个单位 到点 ,连接 .
(1)、求点 、点 的坐标;(2)、将 点向右平移 个单位 到点 ,连接 .①如图1,若 交 轴于点 ,且 ,求 的取值范围;
②如图2,若 , 平分 交 于点 ,已知点 为 轴负半轴上一动点(不与 点重合),射线 交直线 交于点 ,交直线 于点 ,试探究 点在运动过程中 、 、 之间是否有某种确定的数量关系?直接写出你的结论.