湖北省随州市曾都区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-06-10 类型：期末考试

进入出卷网下载

一、单选题

1. 点P（﹣2，1）在平面直角坐标系中所在的象限是( )

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各数是无理数的是（）

A、 $- 8$ B、3 $\sqrt{36}$ C、 $3.14159265$ D、 $\frac{π}{3}$

查看试题解析
3. 如图，点O为直线AB上一点，OC⊥OD．如果∠1=35°，那么∠2的度数是（）

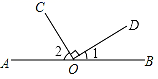A、35° B、45° C、55° D、65°

查看试题解析
4. 把方程 $2 x - y = 3$ 改写成用含 $x$ 的式子表示 $y$ 的形式（）

A、 $y = 2 x - 3$ B、 $y = 2 x + 3$ C、 $x = \frac{1}{2} y + \frac{3}{2}$ D、 $x = \frac{1}{2} y + 3$

查看试题解析
5. 不等式x﹣3≤3x+1的解集在数轴上表示如下，其中正确的是（　　）

A、 B、 C、 D、

查看试题解析
6. 下列结论错误的是（）

A、 $\frac{1}{4}$ 的算术平方根是 $\frac{1}{2}$ B、 $- 2$ 没有立方根 C、 $4$ 的平方根是 $\pm 2$ D、 $0$ 的立方根是 $0$

查看试题解析
7. 中学生骑电动车上学给交通安全带来隐患，为了解中学2 000名学生家长对“中学生骑电动车上学”的态度，从中随机调查400名家长，结果有360名家长持反对态度，则下列说法正确的是（）

A、调查方式是普查 B、该校只有360名家长持反对态度 C、样本是360名家长 D、该校约有90%的家长持反对态度

查看试题解析
8. 如图，下列推理所注的理由正确的是（）

A、∵ $A B ∥ C D$ ，∴ ∠ $1$ ＝∠ $2$ （内错角相等，两直线平行） B、∵∠ $3$ ＝∠ $4$ ，∴ $A B ∥ C D$ （内错角相等，两直线平行） C、∵ $A B ∥ C D$ ，∴∠ $3$ ＝∠ $4$ （两直线平行，内错角相等） D、∵∠ $1$ ＝∠ $2$ ，∴ $A B ∥ C D$ （内错角相等，两直线平行）

查看试题解析
9. 《九章算术》中记载：“今有共买鸡，人出八，盈三；人出七，不足四.问人数、鸡价各几何？”译文：“今天有几个人共同买鸡，每人出8钱，多余3钱，每人出7钱，还缺4钱.问人数和鸡的价钱各是多少？”设人数有x人，鸡的价钱是y钱，可列方程组为（）.

A、 ${\begin{array}{l} 7 x - y = 3 \\ 8 x + 4 = y \end{array}$ B、 ${\begin{array}{l} 7 x + 3 = y \\ 8 x - y = 4 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x + 4 = y \end{array}$ D、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x - y = 4 \end{array}$

查看试题解析
10. 下列结论：
①“相等的角是对顶角”是假命题；

②在同一平面内，若 a⊥b ， $b ⊥ c$ ，则 $a / / c$ ；

③若点 $A (- 3, 2)$ ， $B (- 3, - 2)$ ，则 $A B / / x$ 轴；

④若点 $P (3, - 2)$ ， $Q (m, n)$ ，且 $P Q ⊥ y$ 轴，则 $n = - 2$ .

其中正确结论的个数是（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

11. $0.25$ 的平方根是.

查看试题解析
12. 如图所示的折线图反映的是小明家一周内的购菜花费情况，则在这一周中购菜钱数的最大值与最小值的差为元.

查看试题解析
13. 如图，点 $D$ 是 $C B$ 延长线上一点，如果添加一个条件，使 $E B / / A C$ ，则可添加的条件是（只需添加一个符合题意的条件）.

查看试题解析
14. 如图，三角形 $D E F$ 是由三角形 $A B C$ 通过平移得到，且点 $B$ ， $E$ ， $C$ ， $F$ 在同一条直线上，若 $B F = 14$ ， $E C = 4$ ，则 $B E$ 的长度是.

查看试题解析
15. 在平面直角坐标系中，如果一个点的横、纵坐标均为整数，那么我们称该点是格点.若格点 $P (2 m + 1 ， m - 2)$ 在第四象限，则点 $P$ 到 $x$ 轴的距离为.

查看试题解析
16. 对于实数 $a$ ， $b$ 定义运算“ $◆$ ”： $a ◆ b = {\begin{matrix} a b & (a \geq b) \\ \sqrt{a^{2} + b^{2}} & (a < b) \end{matrix}$ .例如 $4 ◆ 3$ ，因为 $4 > 3$ ，所以 $4 ◆ 3 = 4 \times 3 = 12$ .若 $x$ ， $y$ 满足方程组 ${\begin{array}{l} 4 x - y = 8 \\ x + 2 y = 29 \end{array}$ ，则 $x ◆ y =$ .

查看试题解析

三、解答题

17. 计算或化简：

(1)、计算： $\sqrt{16} - \sqrt[3]{64} + \sqrt[3]{\frac{1}{8}} - \sqrt{\frac{9}{4}}$

(2)、指出下列各实数与数轴上A，B，C，D中哪一点对应；

$- \sqrt{2}$ ， $\sqrt{3}$ ， $- 3$ ， $π$ .

查看试题解析
18. 解方程组或不等式组：

(1)、 ${\begin{array}{l} 2 x + 3 y = 1 \\ x - 2 y = 4 \end{array}$

(2)、 ${\begin{array}{l} 5 x - 17 < 8 (x - 1) \\ x - 6 \leq \frac{x - 10}{2} \end{array}$

查看试题解析
19. 如图，是某动物园的示意图，如果在分别以正东、正北方向为 $x$ 轴、 $y$ 轴正方向的直角坐标系中，猴山和狮虎山的坐标分别是 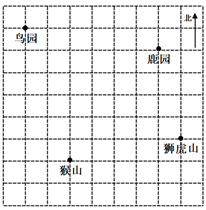$(- 2 ， - 1)$ 和 $(3 ， 0)$ ；

(1)、请在图中画出这个平面直角坐标系；

(2)、写出表示鸟园和鹿园的点的坐标；

(3)、在图中标出熊猫馆 $(2 ， - 2)$ 的位置.

查看试题解析
20. 已知关于x的不等式 $1 - \frac{x}{3} < \frac{m x}{3} - m$ .

(1)、当 $m = 1$ 时，求该不等式的解集；

(2)、若该不等式有解，求m应满足的条件，并求出不等式的解集

查看试题解析
21.

(1)、如图1，在图中画出 $A E ⊥ B C$ ， $C F ⊥ A D$ ，垂足分别为 $E$ ， $F$ ，并通过测量比较 $A E$ 与 $C F$ 的大小；

(2)、如图2，直线 $A B$ ， $C D$ 相交于点 $O$ ， $O B$ 平分 $∠ D O E$ ，若 $∠ C O E ： ∠ E O D = 7 ： 5$ ，求 $∠ A O C$ 的度数.

查看试题解析
22. 为了解疫情防控期间，我区七年级学生网络在线学习时间情况，随机抽取了部分学生进行调查，并绘制了如下不完整的统计图（组数据包括右端点但不包括左端点）.
每天在线学习时间频数分布直方图

每天在线学习时间扇形统计图

(1)、求这次调查抽取了多少名学生？

(2)、补齐频数分布直方图，并求扇形统计图中“ $1.5 - 2$ 小时”部分的圆心角的度数.

(3)、为保护学生视力，规定每天在线学习不得超过 $2$ 小时，那么我区 $6000$ 名七年级学生中大约有多少名学生在线学习时间符合规定？

查看试题解析
23. 某花农培育甲种花木 $2$ 株，乙种花木 $3$ 株，共需成本 $1200$ 元，培育甲种花木 $3$ 株，乙种花木 $1$ 株，共需成本 $1100$ 元.

(1)、求培育甲、乙两种花木每株成本分别为多少元？

(2)、据市场调研， $1$ 株甲种花木售价为 $560$ 元， $1$ 株乙种花木售价为 $380$ 元.该花农培育甲、乙两种花木，若培育乙种花木的株数是甲种花木的 $3$ 倍还多 $10$ 株，那么要使总利润不少于 $15300$ 元，花农至少应培育甲种花木多少株？

查看试题解析
24. 已知 $l_{1} / / l_{2}$ ，点 $A$ ， $C$ 分别在直线 $l_{1}$ ， $l_{2}$ 上，点 $B$ 在直线 $l_{1}$ 与 $l_{2}$ 之间， $∠ B C N < ∠ B A M \leq 90 °$ .

(1)、如图1，

求证： $∠ A B C = ∠ B A M + ∠ B C N$ .

阅读并补齐下列推理过程

过点 $B$ 作 $B G / / N C$ ，因为 $l_{1} / / l_{2}$ ，

所以 $A M / /$ （）

所以 $∠ A B G = ∠ B A M$ ， $∠ C B G = ∠ B C N$ （）

所以 $∠ A B C = ∠ A B G + ∠ C B G = ∠ B A M + ∠ B C N$ .

解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，在学习中要注意体会.

(2)、如图2，点 $D$ ， $E$ 在直线 $l_{1}$ 上， $∠ D B C = ∠ B A M$ ， $B E$ 平分 $∠ A B C$ ，

求证： $∠ D B E = ∠ D E B$ .

(3)、在（2）的条件下，过点 $B$ 作 $B F$ 平分 $∠ C B E$ ，请直接写出使 $B F / / A M$ 时， $∠ B A M$ 与 $∠ B C N$ 之间应具备的关系.

查看试题解析