河南省南阳市卧龙区2021年数学中考一模试卷
试卷更新日期:2021-06-10 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 第四届世界智能大会采取“云上”办会的全新模式呈现,40家直播网站及平台同时在线观看云开幕式暨主题峰会的总人数最高约为58600000人,将58600000用科学记数法表示应为( )A、 B、 C、 D、3. 如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=( )
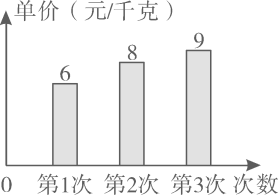 A、9 B、8 C、7 D、64. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若 ,则∠2的度数是( )
A、9 B、8 C、7 D、64. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若 ,则∠2的度数是( )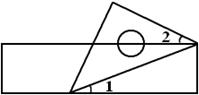 A、15° B、20° C、25° D、40°5. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
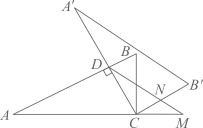
A、15° B、20° C、25° D、40°5. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )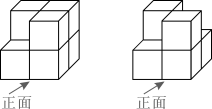 A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同6. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 为了促使药品及医用耗材的价格回归合理水平,减轻群众就医负担,国家近几年大力推进带量采购制度改革,在改革推进的过程中,某药品经过两次降价,每瓶零售价由100元降为81元,已知两次降价的百分率都为x,那么x满足的方程是( )A、 B、 C、 D、8. 定义新运算“ ”:对于任意实数a,b,都有 ,例如 .若 (k为实数)是关于x的方程,则它的根的情况为( )A、有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根9. 如图,将正方形 放在平面直角坐标系中,其中一个顶点放在坐标原点O,将正方形 绕点O逆时针旋转 得到正方形 ,若 ,则点 的坐标为( )
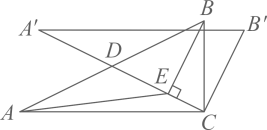
A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同6. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 为了促使药品及医用耗材的价格回归合理水平,减轻群众就医负担,国家近几年大力推进带量采购制度改革,在改革推进的过程中,某药品经过两次降价,每瓶零售价由100元降为81元,已知两次降价的百分率都为x,那么x满足的方程是( )A、 B、 C、 D、8. 定义新运算“ ”:对于任意实数a,b,都有 ,例如 .若 (k为实数)是关于x的方程,则它的根的情况为( )A、有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根9. 如图,将正方形 放在平面直角坐标系中,其中一个顶点放在坐标原点O,将正方形 绕点O逆时针旋转 得到正方形 ,若 ,则点 的坐标为( ) A、 B、 C、 D、10. 如图,E为矩形 边 上的一点,将矩形 沿 折叠,使点D落在 边上点F处,若 ,则 等于( )
A、 B、 C、 D、10. 如图,E为矩形 边 上的一点,将矩形 沿 折叠,使点D落在 边上点F处,若 ,则 等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
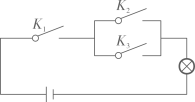
11. 已知变量 与 满足函数关系,且其图象经过原点.请写出一个满足上述要求的函数关系式.12. 若关于 、 的二元一次方程组 的解满足 ,则 的取值范围是.13. 在如图所示的电路图中,当随机闭合开关 , , 中的两个时,能够让灯泡发光的概率为 .
 14. 如图,在 中,按以下步骤作图:①以点A为圆心, 的长为半径画弧,交 于点F;②分别以点F,B为圆心,以大于 的长为半径画弧,两弧在 内交于点G;③作射线 ,交边 于点E,交 于点O,连接 .若 , ,则四边形 的面积为.
14. 如图,在 中,按以下步骤作图:①以点A为圆心, 的长为半径画弧,交 于点F;②分别以点F,B为圆心,以大于 的长为半径画弧,两弧在 内交于点G;③作射线 ,交边 于点E,交 于点O,连接 .若 , ,则四边形 的面积为. 15. 如图,在菱形 中, ,∠ABC=120°以点B为圆心, 长为半径画弧,恰好过顶点D和顶点C,点E,F分别是 上的两点,若 ,则图中阴影部分的面积为.
15. 如图,在菱形 中, ,∠ABC=120°以点B为圆心, 长为半径画弧,恰好过顶点D和顶点C,点E,F分别是 上的两点,若 ,则图中阴影部分的面积为.
三、解答题
-
16. 先化简代数式 ,再从 中选一个恰当的整数作为 的值代入求值.17. 2020年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通,5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域(5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.
请根据图中信息,解答下列问题:
 (1)、图中2020年“新基建”七大领域预计投资规模的平均数约是亿元(结果保留一位小数);(2)、在由“新基建”七大领域预计投资规模组成的扇形统计图中,“新能源汽车充电桩”预计投资规模所占的圆心角约是 (结果保留整数);(3)、甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中,甲选择了“5G基站建设”,乙选择了“人工智能”分别作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么.18. 如图,某工地有一辆吊车, 为车身, 为吊臂,吊车从水平地面C处吊起货物,此时测得吊臂 与水平线的夹角为 .当货物吊至D处时,测得吊臂 与水平线的夹角为 ,且吊臂转动过程中长度始终保持不变,此时D处离水平地面的高度 ,求吊臂的长.(结果保留一位小数,参考数据: , , , , , )
(1)、图中2020年“新基建”七大领域预计投资规模的平均数约是亿元(结果保留一位小数);(2)、在由“新基建”七大领域预计投资规模组成的扇形统计图中,“新能源汽车充电桩”预计投资规模所占的圆心角约是 (结果保留整数);(3)、甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中,甲选择了“5G基站建设”,乙选择了“人工智能”分别作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么.18. 如图,某工地有一辆吊车, 为车身, 为吊臂,吊车从水平地面C处吊起货物,此时测得吊臂 与水平线的夹角为 .当货物吊至D处时,测得吊臂 与水平线的夹角为 ,且吊臂转动过程中长度始终保持不变,此时D处离水平地面的高度 ,求吊臂的长.(结果保留一位小数,参考数据: , , , , , ) 19. 如图,已知一次函数 与反比例函数 的图象交于第一象限内的点 和 ,与x轴交于点A.
19. 如图,已知一次函数 与反比例函数 的图象交于第一象限内的点 和 ,与x轴交于点A. (1)、分别求出这两个函数的表达式;(2)、不等式 的解集是;(3)、若M为线段 上一点,且 轴于点N,则 面积的最大值是.20. 如图,在 中, ,以斜边 上的中线 为直径作 ,分别与边 , 交于点E,F,连接 ,过点F作 的切线交 于点M.
(1)、分别求出这两个函数的表达式;(2)、不等式 的解集是;(3)、若M为线段 上一点,且 轴于点N,则 面积的最大值是.20. 如图,在 中, ,以斜边 上的中线 为直径作 ,分别与边 , 交于点E,F,连接 ,过点F作 的切线交 于点M. (1)、求证: ;(2)、若 的直径是6,填空:
(1)、求证: ;(2)、若 的直径是6,填空:①连接 ,当 时,四边形 是平行四边形;
②连接 , ,当 时,四边形 是正方形.
21. 如图,抛物线与x轴交于点 和点 ,与y轴交于点C,且过点 .点P是抛物线上的动点(不与点D重合),直线 与y轴交于点E. (1)、求抛物线的解析式;(2)、若点P的横坐标为m,则直线 的解析式可用含m的式子表示为;(3)、当点P在直线 下方时,求 面积的最大值.
(1)、求抛物线的解析式;(2)、若点P的横坐标为m,则直线 的解析式可用含m的式子表示为;(3)、当点P在直线 下方时,求 面积的最大值.