福建省漳州市漳浦县初中毕业班2021年数学中考一模试卷
试卷更新日期:2021-06-10 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )A、
 戴口罩讲卫生
B、
戴口罩讲卫生
B、 勤洗手勤通风
C、
勤洗手勤通风
C、 有症状早就医
D、
有症状早就医
D、 少出门少聚集
3. 如图,一个水平放置的正六棱柱,这个正六棱柱的俯视图是( )
少出门少聚集
3. 如图,一个水平放置的正六棱柱,这个正六棱柱的俯视图是( ) A、
A、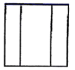 B、
B、 C、
C、 D、
D、 4. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积约为250000m2 , 则250000用科学记数法表示为( )A、25×104m2 B、0.25×106m2 C、2.5×105m2 D、2.5×106m25. 已知 a ≥b,则a ≤-2b,其根据是( )A、不等式的两边都加上(或减去)同一个整式,不等号的方向不变 B、不等式的两边都乘以(或除以)同一个正数,不等号的方向不变 C、不等式的两边都乘以(或除以)同一个负数,不等号的方向改变 D、以上答案均不对6. 运算结果为 的式子是( )A、 B、 C、 D、7. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为 ,则小凡的身高约为( )
4. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积约为250000m2 , 则250000用科学记数法表示为( )A、25×104m2 B、0.25×106m2 C、2.5×105m2 D、2.5×106m25. 已知 a ≥b,则a ≤-2b,其根据是( )A、不等式的两边都加上(或减去)同一个整式,不等号的方向不变 B、不等式的两边都乘以(或除以)同一个正数,不等号的方向不变 C、不等式的两边都乘以(或除以)同一个负数,不等号的方向改变 D、以上答案均不对6. 运算结果为 的式子是( )A、 B、 C、 D、7. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为 ,则小凡的身高约为( ) A、 B、 C、 D、8. 电动车每小时比自行车多行驶了25千米,自行车行驶30千米比电动车行驶40千米多用了1小时,求两车的平均速度各为多少?设自行车的平均速度为x千米/小时,应列方程为( )A、 B、 C、 D、9. 2020年是全面打赢脱贫攻坚战的收官之年,全国832个贫困县全部脱贫摘帽.经2020年精准扶贫后,某贫困村的经济收入增加了一倍.为更好地了解该村的经济收入变化情况,统计了该村精准扶贫前后的经济收入构成比例,得到如下统计图:则下面结论中不正确的是( )
A、 B、 C、 D、8. 电动车每小时比自行车多行驶了25千米,自行车行驶30千米比电动车行驶40千米多用了1小时,求两车的平均速度各为多少?设自行车的平均速度为x千米/小时,应列方程为( )A、 B、 C、 D、9. 2020年是全面打赢脱贫攻坚战的收官之年,全国832个贫困县全部脱贫摘帽.经2020年精准扶贫后,某贫困村的经济收入增加了一倍.为更好地了解该村的经济收入变化情况,统计了该村精准扶贫前后的经济收入构成比例,得到如下统计图:则下面结论中不正确的是( ) A、 精准扶贫后,种植收入减少 B、精准扶贫后,其他收入增加了一倍以上 C、精准扶贫后,养殖收入增加了一倍 D、精准扶贫后,养殖收入与第三产业收入的总和超过了经济收入的一半10. 二次函数 ,若 为正整数,且 随 的增大而减小,则 的取值范围是( )A、 B、 C、 D、
A、 精准扶贫后,种植收入减少 B、精准扶贫后,其他收入增加了一倍以上 C、精准扶贫后,养殖收入增加了一倍 D、精准扶贫后,养殖收入与第三产业收入的总和超过了经济收入的一半10. 二次函数 ,若 为正整数,且 随 的增大而减小,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
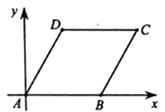
11. 分解因式: .12. 计算: .13. 从 、-1、1、2中任取两个数求和作为 ,使抛物线 的开口向上的概率为.14. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形 中, , .如图,以点 为坐标原点,建立平面直角坐标系,使得边 在 轴正半轴上,则点 的坐标是.
 15. 一块直角三角板的 角的顶点 落在 上,两边分别交 于 、 两点,若弦 ,则 的半径为.
15. 一块直角三角板的 角的顶点 落在 上,两边分别交 于 、 两点,若弦 ,则 的半径为.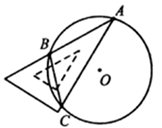 16. 平面直角坐标系 中,点 在第二象限, 轴于点 ,反比例函数 的图象经过 的中点 ,交 于点 ,若 的面积为4,则 .
16. 平面直角坐标系 中,点 在第二象限, 轴于点 ,反比例函数 的图象经过 的中点 ,交 于点 ,若 的面积为4,则 .
三、解答题
-
17. 解不等式组:18. 如图,在 中,点 在 边上,点 在 边上,且 .求证:
 19. 先化简,再求值: ,其中 .20. 《杨辉算法》中有这么一道题:“直田积九十六步,只云长阔共二十步,问长多几何?”意思是:一块矩形田地的面积为96平方步,只知道它的长与宽共20步,问它的长比宽多了多少步?21. 如图,在矩形 中, , ,点 是 的中点.
19. 先化简,再求值: ,其中 .20. 《杨辉算法》中有这么一道题:“直田积九十六步,只云长阔共二十步,问长多几何?”意思是:一块矩形田地的面积为96平方步,只知道它的长与宽共20步,问它的长比宽多了多少步?21. 如图,在矩形 中, , ,点 是 的中点.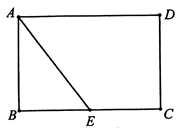 (1)、尺规作图:在 上求作一点 ,使 ;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求 的长.22. 某中学到天福石雕园开展研学实践活动,在参观了“民族英雄郑成功”雕像后.小颖想测量“民族英雄郑成功”雕像 的高度,如图,她在雕像前 处用测倾器测得顶端 的仰角为 ,底端 的俯角为 ;又在同一水平线上的 处用测倾器测得顶端 的仰角为 ,已知 ,求雕像 的高度.( ,结果精确到 )
(1)、尺规作图:在 上求作一点 ,使 ;(保留作图痕迹,不写作法)(2)、在(1)的条件下,求 的长.22. 某中学到天福石雕园开展研学实践活动,在参观了“民族英雄郑成功”雕像后.小颖想测量“民族英雄郑成功”雕像 的高度,如图,她在雕像前 处用测倾器测得顶端 的仰角为 ,底端 的俯角为 ;又在同一水平线上的 处用测倾器测得顶端 的仰角为 ,已知 ,求雕像 的高度.( ,结果精确到 ) 23. 电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
23. 电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.表1:四种款式电脑的利润
电脑款式
A
B
C
D
利润(元/台)
160
200
240
320
表2:甲、乙两店电脑销售情况
电脑款式
A
B
C
D
甲店销售数量(台)
20
15
10
5
乙店销售数量(台)8
8
10
14
18
试运用统计与概率知识,解决下列问题:
(1)、从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为;(2)、经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.
