2021年高考文数真题试卷(全国甲卷)
试卷更新日期:2021-06-10 类型:高考真卷
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 设集合 ,则 ( )A、 B、 C、 D、2. 为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:

根据此频率分布直方图,下面结论中不正确的是( )
A、该地农户家庭年收入低于4.5万元的农户比率估计为6% B、该地农户家庭年收入不低于10.5万元的农户比率估计为10% C、估计该地农户家庭年收入的平均值不超过6.5万元 D、估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间3. 已知 ,则z=( )A、-1- i B、-1+ i C、- +i D、- -i4. 下列函数中是增函数的为( )A、 B、 C、 D、5. 点 到双曲线 的一条渐近线的距离为( )A、 B、 C、 D、6. 青少年视力是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记数法的数据V满足L=5+lgV。已知某同学视力的五分记录法的数据为4.9,则其视力的小数记数法的数据约为( )( ≈1.259)A、1.5 B、1.2 C、0.8 D、0.67. 在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正试图如右图所示,则相应的侧视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 在 中,已知 ,则 ( )A、1 B、 C、 D、39. 记 为等比数列 的前 项和.若 ,则 ( )A、7 B、8 C、9 D、1010. 将3个1和2个0随机排成一行,则2个0不相邻的概率为( )A、0.3 B、0.5 C、0.6 D、0.811. 若 , ,则 ( )A、 B、 C、 D、12. 设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若 ( )A、 B、 C、 D、
8. 在 中,已知 ,则 ( )A、1 B、 C、 D、39. 记 为等比数列 的前 项和.若 ,则 ( )A、7 B、8 C、9 D、1010. 将3个1和2个0随机排成一行,则2个0不相邻的概率为( )A、0.3 B、0.5 C、0.6 D、0.811. 若 , ,则 ( )A、 B、 C、 D、12. 设f(x)是定义域为R的奇函数,且f(1+x)=f(-x).若 ( )A、 B、 C、 D、二、填空题:本题共4小题,每小题5分,共20分。
-
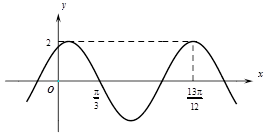
13. 若向量 满足| |=3,| |=5, ⋅ =1,则| |= .14. 已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .15. 已知函数 的部分图像如图所示,则 = .
 16. 已知F1 , F2为椭圆C: 的两个焦点,P,Q为C上关于坐标原点对称的两点,且 ,则四边形PF1QF2的面积为。
16. 已知F1 , F2为椭圆C: 的两个焦点,P,Q为C上关于坐标原点对称的两点,且 ,则四边形PF1QF2的面积为。三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
-
17. 甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
一级品
二级品
合计
甲机床
150
50
200
乙机床
120
80
200
合计
270
130
400
(1)、甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)、能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附:
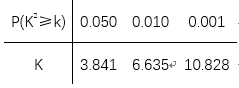 18. 记 为 的前 项和,已知 ,且数列 是等差数列.证明: 是等差数列.19. 已知直三棱柱 中,侧面 为正方形. 分别为 和 的中点, .
18. 记 为 的前 项和,已知 ,且数列 是等差数列.证明: 是等差数列.19. 已知直三棱柱 中,侧面 为正方形. 分别为 和 的中点, .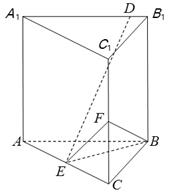 (1)、求三棱锥F-EBC的体积;(2)、已知 为棱 上的点,证明: .20. 设函数 ,其中a>0.(1)、讨论f(x)的单调性;(2)、若y=f(x)的图像与x轴没有公共点,求a的取值范围.21. 抛物线C的顶点为坐标原点O,焦点在x轴上,直线L:x = 1交C于P,Q两点,且OP丄OQ.已知点M(2,0),且 M与L相切,(1)、求 M的方程;(2)、设A1 , A2 , A3 , 是C上的三个点,直线A1 A2 , A1 A3均与 M相切,判断A2A3与 M的位置关系,并说明理由.
(1)、求三棱锥F-EBC的体积;(2)、已知 为棱 上的点,证明: .20. 设函数 ,其中a>0.(1)、讨论f(x)的单调性;(2)、若y=f(x)的图像与x轴没有公共点,求a的取值范围.21. 抛物线C的顶点为坐标原点O,焦点在x轴上,直线L:x = 1交C于P,Q两点,且OP丄OQ.已知点M(2,0),且 M与L相切,(1)、求 M的方程;(2)、设A1 , A2 , A3 , 是C上的三个点,直线A1 A2 , A1 A3均与 M相切,判断A2A3与 M的位置关系,并说明理由.四、[选修4-4:坐标系与参数方程]。