江苏省扬州市宝应县2021年数学中考一模试卷
试卷更新日期:2021-06-10 类型:中考模拟
一、单选题
-
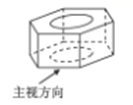
1. 下列各数中,负数是( )A、﹣(﹣2) B、|﹣2| C、﹣23 D、(﹣2)22. 下列各式计算结果是a6的是( )A、a3+a3 B、a12÷a2 C、a2•a3 D、(﹣a3)23. 如图所示的六角螺母,其俯视图是( )
 A、
A、 B、
B、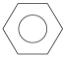 C、
C、 D、
D、 4. 如图,直线a//b,直线l与直线a、b分别交于点A、B,若∠1=54°,则∠2等于( )
4. 如图,直线a//b,直线l与直线a、b分别交于点A、B,若∠1=54°,则∠2等于( ) A、126° B、134° C、130° D、144°5. 某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:
A、126° B、134° C、130° D、144°5. 某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:①从扇形图中分析出最受学生欢迎的种类
②去图书馆收集学生借阅图书的记录
③绘制扇形图来表示各个种类所占的百分比
④整理借阅图书记录并绘制频数分布表
正确统计步骤的顺序是( )
A、②→③→①→④ B、③→④→①→② C、①→②→④→③ D、②→④→③→①6. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、7. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )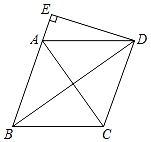 A、 B、 C、4 D、8. 把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y=﹣a(x﹣1)2+2a,若(m﹣1)a+b+c≤0,则m的最大值是( )A、0 B、1 C、2 D、4
A、 B、 C、4 D、8. 把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y=﹣a(x﹣1)2+2a,若(m﹣1)a+b+c≤0,则m的最大值是( )A、0 B、1 C、2 D、4二、填空题
-
9. 分解因式: =10. 当x=时,代数式 值为0.11. 从甲、乙、丙三人中选一人参加环保知识抢答赛,经过两轮初赛,他们的平均成绩都是89,方差分别是S甲2=1.2,S乙2=3.3,S丙2=11.5.你认为适合选参加决赛.12. 如果关于x的方程x2+3x﹣k=0有两个不相等的实数根,那么k的取值范围是 .13. 如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=.
 14. 《孙子算经》是中国古代经典的数学著作,其中有首歌谣,今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?其大意是,有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为.15. 如图,▱ABCD的顶点A、B在x轴上,顶点D在y轴上,顶点C在第一象限,反比例函数 (x>0)的分支过点C,若▱ABCD的面积为3,则k=.
14. 《孙子算经》是中国古代经典的数学著作,其中有首歌谣,今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?其大意是,有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为.15. 如图,▱ABCD的顶点A、B在x轴上,顶点D在y轴上,顶点C在第一象限,反比例函数 (x>0)的分支过点C,若▱ABCD的面积为3,则k=. 16. 将一副直角三角板拼成如图所示的四边形ABCD,一边重合,若∠CAB=45°,∠CAD=30°,连接BD,则tan∠DBC=.
16. 将一副直角三角板拼成如图所示的四边形ABCD,一边重合,若∠CAB=45°,∠CAD=30°,连接BD,则tan∠DBC=.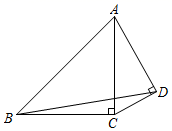 17. 如图,△ABC中,∠ABC=90°,以AC为斜边在△ABC的外部作等腰Rt△ADC,若AB= ,BD= ,则BC=.
17. 如图,△ABC中,∠ABC=90°,以AC为斜边在△ABC的外部作等腰Rt△ADC,若AB= ,BD= ,则BC=.
三、解答题
-
18.(1)、计算:4sin60°﹣ +( ﹣1)0;(2)、化简:(x+y)2﹣(x﹣y)(x+y).19. 解不等式组 ,并写出x的所有整数解.20. 某校在以“青春心向党,筑梦新时代”为主题的校园文化艺术节期间,举办了A合唱,B舞蹈,C书法,D演讲共四个项目的比赛,要求每位学生必须参加且仅参加一项,小丽随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图,请根据统计图中信息解答下列问题:
 (1)、本次调查的学生总人数是人;扇形统计图中“D”部分的圆心角是°.(2)、请将条形统计图补充完整;(3)、若全校共有1600名学生,请估计该校报名参加书法和演讲比赛的学生共有多少人?21. 某校有4个测温通道,分别记为A、B、C、D,学生可随机选取其中的一个通道测温进校园,某日早晨该校所有学生体温正常.(1)、小王同学该日早晨进校园时,选择A通道测温进校园的概率是;(2)、小王和小李两同学该日早晨进校园时,请用面树状图或列表法求选择不同通道测温进校园的概率.22. 如图,点B、F、C、E在同一直线上,且BF=CE,点A、D分别在直线BE的两侧,AB//DE,∠A=∠D.
(1)、本次调查的学生总人数是人;扇形统计图中“D”部分的圆心角是°.(2)、请将条形统计图补充完整;(3)、若全校共有1600名学生,请估计该校报名参加书法和演讲比赛的学生共有多少人?21. 某校有4个测温通道,分别记为A、B、C、D,学生可随机选取其中的一个通道测温进校园,某日早晨该校所有学生体温正常.(1)、小王同学该日早晨进校园时,选择A通道测温进校园的概率是;(2)、小王和小李两同学该日早晨进校园时,请用面树状图或列表法求选择不同通道测温进校园的概率.22. 如图,点B、F、C、E在同一直线上,且BF=CE,点A、D分别在直线BE的两侧,AB//DE,∠A=∠D. (1)、求证:△ABC≌△DEF;(2)、连接AD交BE于点O,若AO=BO,请补全图形并证明:四边形ABDE是矩形.23. 为庆祝中国共产党成立100周年,扬州漆器厂接到制作960件漆器纪念贺礼订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多50%,结果提前10天完成任务.原来每天制作多少件?24. 如图,△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,以点O为圆心,OC长为半径作圆.
(1)、求证:△ABC≌△DEF;(2)、连接AD交BE于点O,若AO=BO,请补全图形并证明:四边形ABDE是矩形.23. 为庆祝中国共产党成立100周年,扬州漆器厂接到制作960件漆器纪念贺礼订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多50%,结果提前10天完成任务.原来每天制作多少件?24. 如图,△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,以点O为圆心,OC长为半径作圆. (1)、求证:AB是⊙O的切线;(2)、若∠B=30°,BC=12,求阴影部分面积.25. 从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这个三角形称为准黄金三角形.
(1)、求证:AB是⊙O的切线;(2)、若∠B=30°,BC=12,求阴影部分面积.25. 从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这个三角形称为准黄金三角形. (1)、请判断:含30°角的直角三角形(填“是”或“不是”)准黄金三角形;(2)、如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:△ABC是准黄金三角形;(3)、如图2,△ABC是准黄金三角形,AC=3,BC= ,且△ACD是以CD为底边的等腰三角形,求CD的长.26. 某商店销售进价为30元/件的某种商品,在第x(1≤x≤90)天的售价与销量的相关信息如下表:
(1)、请判断:含30°角的直角三角形(填“是”或“不是”)准黄金三角形;(2)、如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:△ABC是准黄金三角形;(3)、如图2,△ABC是准黄金三角形,AC=3,BC= ,且△ACD是以CD为底边的等腰三角形,求CD的长.26. 某商店销售进价为30元/件的某种商品,在第x(1≤x≤90)天的售价与销量的相关信息如下表:时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
设销售商品的每天利润为y元.
(1)、求出y与x的函数关系式;(2)、问该商品第几天时,当天销售利润最大,最大利润是多少?(3)、现该商店决定每销售1件该商品就捐赠a元(a>0)给贫困地区,在销售的前50天内该商店当日最大利润为5832元,求a的值.27. 如图,在△ABC中,AB=AC,BC=8,tanC= ,点M、N分别在AB、BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B. (1)、求点P在BN上运动时,点P与点A的最短距离;(2)、若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)、求整个运动过程点Q运动的路径长.
(1)、求点P在BN上运动时,点P与点A的最短距离;(2)、若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)、求整个运动过程点Q运动的路径长.