江苏省盐城市阜宁县2021年数学中考一模试卷
试卷更新日期：2021-06-10 类型：中考模拟
一、单选题
-
1. 比﹣2大2的数是（ ）A、4 B、0 C、﹣2 D、﹣42. 在平面直角坐标系中，点B的坐标是（4，﹣1），点A与点B关于x轴对称，则点A的坐标是（ ）
A、（4，1） B、（﹣1，4） C、（﹣4，﹣1） D、（﹣1，﹣4）3. 2020年11月10日，中国“奋斗者”号载人潜水器在马里亚纳海沟成功坐底，坐底深度10909米，创造中国载人深潜新纪录.将10909用科学记数法表示为（ ）A、109.09×102 B、10.909×103 C、1.0909×104 D、0.10909×1054. 计算a6÷a3,正确的结果是（ ）A、2 B、3a C、a2 D、a35. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“青”字所在面相对的面上的汉字是（ ）
A、青 B、春 C、梦 D、想6. 如图是成都市某周内日最高气温的折线统计图，关于这7天的日最高气温的说法正确的是（ ）
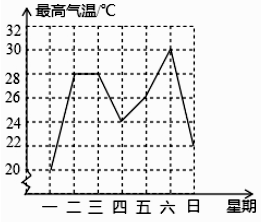A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃7. 如图，圆周角∠ABC＝26°，过点C作⊙O的切线交OA的延长线于点D，则∠D的大小为（ ）
A、26° B、38° C、48° D、52°8. 函数y＝kx﹣2与y＝ （k≠0）在同一坐标系内的图象可能是（ ）A、
B、
C、
D、
二、填空题
-
9. 若二次根式 有意义，则x的取值范围是 ．10. 如图，已知直线AB、CD被直线AE所截，AB∥CD，∠2＝130°，则∠1＝.
11.如图，在“ ”网格中，有 个涂成黑色的小方格．若再从余下的 个小方格中随机选取 个涂成黑色，则完成的图案为轴对称图案的概率是 ．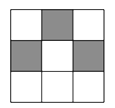
12. 已知am＝4，an＝2，则a2m﹣n的值为.13. 已知α，β是方程x2﹣4x﹣5＝0的两个实数根，则α2﹣2αβ﹣4α的值为.14. 如图，直线AB与CD分别与⊙O 相切于B、D两点，且AB⊥CD，垂足为P，连接BD.若BD＝4，则阴影部分的面积为.
15. 据美国约翰斯•霍普金斯大学发布的全球新冠肺炎数据统计系统，截至美国东部时间3月28日晚6时，全美共报告新冠肺炎确诊人数超过3025万，死亡超过54.9万，已知有一人患了新冠肺炎，经过两轮传染后，共有144人患了新冠肺炎，每轮传染中平均每人传染了人.16. 如图，在直角坐称系中，半径为1的⊙A圆心A的坐标为（﹣1，0），点P为直线y＝﹣ x+2上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是.
三、解答题
-
17. 计算： +2sin30°+（π﹣3.14）0.18. 先化简，再求代数式 的值，其中19. 某学校开展了防疫知识的宣传教育活动.为了解这次活动的效果，学校从全校1500名学生中随机抽取部分学生进行知识测试（测试满分100分，得分x均为不小于60的整数），并将测试成绩分为四个等第：基本合格（60≤x＜70），合格（70≤x＜80），良好（80≤x＜90），优秀（90≤x≤100），制作了如图统计图（部分信息未给出）.
由图中给出的信息解答下列问题：
(1)、求测试成绩为合格的学生人数，并补全频数直方图.(2)、求扇形统计图中“良好”所对应的扇形圆心角的度数.(3)、这次测试成绩的中位数是什么等第？(4)、如果全校学生都参加测试，请你根据抽样测试的结果，估计该校获得优秀的学生有多少人？20. 小明代表学校参加“我和我的祖国”主题宣传教育活动．该活动分为两个阶段，第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目（依次用 、 、 表示），第二阶段有“故事演讲”、“诗歌朗诵”2个项目（依次用 、 表示），参加人员在每个阶段各随机抽取一个项目完成．用画树状图或列表的方法列出小明参加项目的所有等可能的结果，并求小明恰好抽中 、 两个项目的概率．21. 如图，在△ABC中，AB＝AC，AD为BC边上的中线.
(1)、用直尺和圆规作DE⊥AB于点E（不要求写作法，保留作图痕迹）并证明△BDE∽△CAD.(2)、若AB＝13，BC＝10，求线段DE的长.22. 为打造绿色生态公园，白天鹅公园二期扩建中购买了甲、乙两种树苗.已知一棵甲种树苗比一棵乙种树苗贵2元，购买甲种树苗的费用和购买乙种树苗的费用分别是7000元和5000元.(1)、若两种树苗购买的棵数一样多，求甲种树苗的单价；(2)、若两种树苗共购买2200棵，且购买两种树苗的总费用不超过12000元，根据（1）中两种树苗的单价，求乙种树苗至少购买多少棵.23. 如图，在四边形 中， ， . 是四边形 内一点，且 .
求证：
(1)、（1） ；(2)、四边形 是菱形.24. 随着中国经济的快速发展以及科技水平的飞速提高，中国高铁正迅速崛起．高铁大大缩短了时空距离，改变了人们的出行方式．如图，A，B两地被大山阻隔，由A地到B地需要绕行C地，若打通穿山隧道，建成A，B两地的直达高铁可以缩短从A地到B地的路程．已知：∠CAB=30°，∠CBA=45°，AC=640公里，求隧道打通后与打通前相比，从A地到B地的路程将约缩短多少公里？（参考数据： ≈1.7， ≈1.4）
25. 如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点A和点D的圆，圆心O在线段AB上，⊙O交AB于点E，交AC于点F.
(1)、判断BC与⊙O的位置关系，并说明理由；(2)、若AD＝8，AE＝10，求BD的长.26. 定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)、如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E.(2)、如图2，四边形ABCD内接于⊙O， ＝ ，四边形ABCD的外角平分线DF交⊙O于点F，连结BF并延长交CD的延长线于点E.求证：∠BEC是△ABC中∠BAC的遥望角.(3)、如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径.①求∠AED的度数；
②若AB＝8，CD＝5，求△DEF的面积.
27. 已知抛物线y＝ax2＋bx＋6（a≠0）交x轴于点A(6，0)和点B(－1，0)，交y轴于点C.
(1)、求抛物线的解析式和顶点坐标；(2)、如图（1），点P是抛物线上位于直线AC上方的动点，过点P分别作x轴，y轴的平行线，交直线AC于点D，E，当PD＋PE取最大值时，求点P的坐标；(3)、如图（2），点M为抛物线对称轴l上一点，点N为抛物线上一点，当直线AC垂直平分△AMN的边MN时，求点N的坐标.