江苏省宿迁市泗洪县2021年数学中考一模试卷
试卷更新日期:2021-06-10 类型:中考模拟
一、单选题
-
1. 下列各数中,比-2小的数是( )A、 B、 C、 D、2. 数轴上表示-8和2点分别是A和B,则线段AB的长度是( )A、6 B、-6 C、10 D、-103. 方程x2=2x的解是( )A、x=0 B、x=2 C、x1=0,x2=2 D、x1=0,x2=4. 下列计算中,正确的是( )A、(2a)3=2a3 B、a3+a2=a5 C、a8÷a4=a2 D、(a2)3=a65. 如图,在 中, , , ,以点 为圆心,3为半径的圆与 所在直线的位置关系是( )
 A、相交 B、相离 C、相切 D、无法判断6. 下列函数中,当 时, 随 增大而增大的是( )A、 B、 C、 D、7. 某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
A、相交 B、相离 C、相切 D、无法判断6. 下列函数中,当 时, 随 增大而增大的是( )A、 B、 C、 D、7. 某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:甲
乙
丙
丁
平均数/环
9.7
9.5
9.5
9.7
方差/环2
5.1
4.7
4.5
4.5
请你根据表中数据选一人参加比赛,最合适的人选是( )
A、甲 B、乙 C、丙 D、丁8. 某单位为某中学捐赠了一批新桌椅.学校组织七年级300名学生搬桌椅,规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )A、80 B、120 C、160 D、200二、填空题
-
9. 要使式子 有意义,则x的取值范围是 .10. 若一个多边形的每一个外角都为 则该多边形为边形.11. 将抛物线 沿y轴向下平移3个单位,则平移后抛物线的顶点坐标为.12. 抛一枚质地均匀的硬币,前 次都是反面朝上,则抛第 次时反面朝上的概率是.13. 用一个半径为 半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为 . (精确到 ).14. 如图,⊙O 的直径AB=12,CD 是⊙O 的弦,CD⊥AB,垂足为P,且BP∶AP=1∶5, 则CD 的长为.
 15. 如图,四边形 是 的内接四边形,且 , ,垂足分别为 ,若 ,则 .
15. 如图,四边形 是 的内接四边形,且 , ,垂足分别为 ,若 ,则 . 16. 已知 个连续整数的和为 ,它们的平方和是 ,且 .则 .17. 在平面直角坐标系xOy中,⊙O的半径为13,直线y=kx﹣3k+4与⊙O交于B,C两点,则弦BC长的最小值等于.18. 如图,在凸四边形 中, , ,则线段 的长等于 .
16. 已知 个连续整数的和为 ,它们的平方和是 ,且 .则 .17. 在平面直角坐标系xOy中,⊙O的半径为13,直线y=kx﹣3k+4与⊙O交于B,C两点,则弦BC长的最小值等于.18. 如图,在凸四边形 中, , ,则线段 的长等于 . 19. 如图所示,二次函数 的图象与 轴交于点 ,对称轴为直线 .则方程 的两个根为.
19. 如图所示,二次函数 的图象与 轴交于点 ,对称轴为直线 .则方程 的两个根为. 20. 央视前著名主持人崔永元曾自曝,自小不爱数学,视数学为灾难,成年后还做过数学衢梦,心狂跳不止:梦见数学考试了,水池有个进水管,5小时可注满,池底有一个出水管,8小时可放完满池水若同时开打进水管和出水管,多少小时可注满空池?“神经吧,你到底想放水还是注水?这题也太变态了!”崔永元很困惑.
20. 央视前著名主持人崔永元曾自曝,自小不爱数学,视数学为灾难,成年后还做过数学衢梦,心狂跳不止:梦见数学考试了,水池有个进水管,5小时可注满,池底有一个出水管,8小时可放完满池水若同时开打进水管和出水管,多少小时可注满空池?“神经吧,你到底想放水还是注水?这题也太变态了!”崔永元很困惑.这类放水注水题,相信同学们小学时就接触不少,其实这只是个数学模型,用来形象地刻画“增加量消耗量=改变量”,这类数量关系可以用于处理现实生活中的大量问题,突出数学建模、数学抽象等核心素养,体现数学魅力所在.
例如,某仓库,从某时刻开始4小时内只进货不出货,在随后的8小时内同时进出货,接着按此进出货速度,不进货,直到把仓库中的货出完假设每小时进、出货量是常数,仓库中的货物量 (吨)与时间 (时)之间的部分关系如图,那么从不进货起小时后该仓库内的货恰好运完.

三、解答题
-
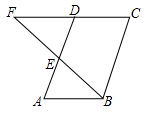
21.(1)、计算: ;(2)、化简: .22. 解方程:(1)、 ;(2)、 .23. 如图,在 中,E是边 的中点, 的延长线与 的延长线相交于点F.
求证: .
 24. 学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表
24. 学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表借阅图书的次数
0次
1次
2次
3次
4次及以上
人数
7
13
a
10
3
请你根据统计图表中的信息,解答下列问题:
 (1)、a= , .(2)、该调查统计数据的中位数是 , 众数是 .
(1)、a= , .(2)、该调查统计数据的中位数是 , 众数是 .
(3)、请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)、若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
25. 关于x的一元二次方程x2+2x﹣(n﹣1)=0有两个不相等的实数根.(1)、求n的取值范围;(2)、若n为取值范围内的最小整数,求此方程的根.26. 当自变量 时,二次函数的值最小,最小值为-3,且这个函数的图象与 轴的一个交点的横坐标为1.(1)、求这个二次函数的表达式;(2)、求这个函数的图象与 轴交点的坐标.27. 一块含有 角的三角板 如图所示,其中 , , .将此三角板在平面内绕顶点 旋转一周. (1)、画出边 旋转一周所形成的图形;(2)、求出该图形的面积.28. 某商店销售一种服装,已知该服装每件成本为50元.经市场调研,售价为每件60元时,可销售800件;售价每提高5元,销售量将减少100件.
(1)、画出边 旋转一周所形成的图形;(2)、求出该图形的面积.28. 某商店销售一种服装,已知该服装每件成本为50元.经市场调研,售价为每件60元时,可销售800件;售价每提高5元,销售量将减少100件.问:商店销售这批服装计划获利12000元,应如何进货?每件售价多少元?
29. 如图, 的直径 , 和 是它的两条切线, 与 相切于点 ,并与 , 分别相交于 , 两点,设 , ,求 关于 的函数表达式,并在坐标系中画出它的图象.
 30. 在抛物线 中,规定:(1)符号 称为该抛物线的“抛物线系数”;(2)如果一条抛物线与 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
30. 在抛物线 中,规定:(1)符号 称为该抛物线的“抛物线系数”;(2)如果一条抛物线与 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.完成下列问题:
(1)、若一条抛物线的系数是 ,则此抛物线的函数表达式为 , 当 满足时,此抛物线没有“抛物线三角形”;(2)、若抛物线 的“抛物线三角形”是等腰直角三角形,求出抛物线系数为 的“抛物线三角形”的面积;(3)、在抛物线 中,系数 均为绝对值不大于 的整数,求该抛物线的“抛物线三角形”是等腰直角三角形的概率.