江苏省泰州市兴化市2021年数学中考一模试卷

试卷更新日期：2021-06-10 类型：中考模拟

进入出卷网下载

一、单选题

1. -5的倒数是（）

A、5 B、-5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 一个用于防震的L形包装塑料泡沫如图所示，则该物体的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 若m表示任意实数，则下列计算一定正确的是（）

A、 $m^{2} \cdot m^{3} = m^{5}$ B、 $m^{5} \div m = 5$ C、 $m^{2} + m^{2} = m^{4}$ D、 ${(m^{2})}^{3} = m^{5}$

查看试题解析
4. 如图，转盘中6个扇形的面积都相等.任意转动转盘1次，当转盘停止转动时，事件“指针所落扇形中的数小于3”的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、2

查看试题解析
5. 一个多边形的每一个内角都是108°，则它的边数为（）

A、4 B、5 C、6 D、8

查看试题解析
6. 已知二次函数y＝x²－bx＋c的图象经过A（1，n），B（3，n），且与x轴只有一个交点，则n的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析

二、填空题

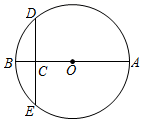
7. 9的算术平方根是．

查看试题解析
8. 若分式 $\frac{1}{x - 3}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
9. 因式分解： $a x^{2} - a$ = ．

查看试题解析
10. 据泰州市统计局反馈，2020年，兴化市实现地区生产总值 $90 100000000$ 元.用科学记数法把 $90 100000000$ 表示为.

查看试题解析
11. 不等式组 ${\begin{array}{l} x > - 2 \\ x \leq 3 \end{array}$ 的解集为.

查看试题解析
12. 等腰三角形的两边长为3和7，则第三边长为．

查看试题解析
13. 学校广播站招聘记者时，综合成绩由3部分组成：采访写作占50%，电脑操作占20%，创意设计占30%.应聘者小明同学这3项成绩依次为90分、60分、70分，则小明同学的综合成绩为分.

查看试题解析
14. 将一张圆形纸片等分成3张扇形纸片，从中取一张，恰好能围成底面积为25π cm²的圆锥模型的侧面，则该圆锥模型的母线长为cm.

查看试题解析
15. 如图，⊙O的半径OA＝15，弦DE⊥AB于点C，若OC：BC＝3：2，则DE的长为.

查看试题解析
16. 如图，点P是直线y﹦﹣2x位于第二象限上一点，过点P分别作两条坐标轴的平行线，与双曲线 $y = \frac{k}{x} (k > 0)$ 相交于点A、B，则直线AB与x轴所夹锐角的正弦值为.

查看试题解析

三、解答题

17.

(1)、计算： $(\sqrt{12} - \sqrt{\frac{1}{3}}) \times \sqrt{6}$ ；

(2)、解方程： $\frac{3 - x}{x - 4} + \frac{1}{4 - x} = 1$ .

查看试题解析
18. 一只不透明的袋子里共有2个白球，1个红球，它们除颜色外均相同.

(1)、求从袋子中任意摸出一个球是白球的概率；

(2)、从袋子中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出一个球.用“表格”或“树状图”列出所有等可能的结果，并求两次都摸到白球的概率.

查看试题解析
19. 某商店用2900元购进甲、乙两种饮料共150箱，饮料的成本价与销售价如下：

饮料品种

成本价（元/箱）

销售价（元/箱）

甲

18

24

乙

22

25

(1)、商场购进甲、乙两种饮料各多少箱？

(2)、该商场销售完这150箱饮料后可获得利润多少元？

查看试题解析
20. 如图，AB是⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠CAD＝∠D，给出下列三个信息：①sin∠CAB＝ $\frac{1}{2}$ ；②BO＝BD；③DC是⊙O的切线.

(1)、请在信息①或②中选择一个作为条件，剩下的两个信息中选择一个作为结论，组成一个真命题.你选择的条件是，结论是（只要填写序号）.

(2)、证明（1）中你写出的真命题.

查看试题解析
21. 如图，Rt△ABC中，∠ACB＝90°，用直尺与圆规在BC的延长线上作点E，连接AE，使∠EAC＝∠ABC.

(1)、不要求写出作图步骤，但保留作图痕迹；

(2)、若AC＝3，∠CAB的正切值为 $\frac{4}{3}$ ，求CE的值.

查看试题解析

22. 在研发某种新冠疫苗的一次动物实验中，将200只基因编辑小鼠分成20组，每组10只.选取其中10个组作为接种批次，给每只小鼠注射疫苗，其余作为对照批次，不注射疫苗.实验后统计发现，接种批次共有13只小鼠发病，发病率为0.13.对照批次小鼠发病情况如下表所示.

对照批次编号（组）	1	2	3	4	5	6	7	8	9	10
发病小鼠数（只）	3	5	7	3	8	4	8	5	5	6

(1)、①对照批次发病小鼠数的中位数是，众数是；

②求对照批次发病小鼠的总只数；

(2)、流行病学中，疫苗在一定范围内能保护某个群体的机率叫做疫苗保护率，其计算方法是：疫苗保护率＝

\frac{对 照 批 次 发 病 率 - 接 种 批 次 发 病 率}{对 照 批 次 发 病 率}

.由此可得这种新冠疫苗保护率是多少（结果精确到0.01）？

查看试题解析

23. 如图是一辆自卸式货车的示意图，矩形货厢ABCD的长AB＝4 m.卸货时，货厢绕A点处的转轴旋转，货厢底部A、B两点在垂直方向上的距离与水平距离之比记作i.A点处的转轴与后车轮转轴（点M处）的水平距离叫做安全轴距，测得该车的安全轴距为0.7 m.货厢对角线AC、BD的交点G可视为货厢的重心，测得∠ACB＝66.4°.假设该车在平地上进行卸货作业（即AN为水平线）.

(1)、若i＝1： $\sqrt{3}$ ，求A、B两点在垂直方向上的距离；

(2)、卸货时发现，当A、G两点的水平距离小于安全轴距时，会发生车辆倾覆事故.若i＝1：1，该货车会发生上述事故吗？试说明你的理由.（参考数据：sin66.4°≈0.92，cos66.4°≈0.40，cos68.6°≈0.36，tan68.6°≈0.55）

查看试题解析
24. 如图，以菱形OABC的顶点O为坐标原点建立平面直角坐标系，点A在x轴的正半轴上，点B、C在第一象限内.反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限内的图
像过点C，交直线OB于点D.点B的坐标为（8，4）.

(1)、求直线OB的函数表达式；

(2)、求点D的坐标.

查看试题解析
25. 二次函数 $y_{1} = x^{2} + (2 k - 1) x + 2 k$ 的图象为 $C_{1}$ ，二次函数 $y_{2} = - x^{2} + (2 k + 1) x + 2 k$ 的图象为 $C_{2}$ .

(1)、当点 $A (k ， 0)$ 在 $C_{1}$ 上时，求 $k$ 的值；

(2)、点 $B (t ， 0)$ 在 $x$ 轴上，过点 $B$ 作 $y$ 轴的平行线，与 $C_{1}$ 和 $C_{2}$ 的交点纵坐标分别为 $y_{1}$ 、 $y_{2}$ .当 $t > 1$ 时，试比较 $y_{1}$ 与 $y_{2}$ 的大小，并说明理由；

(3)、不论 $k$ 为何值，图象 $C_{1}$ 都经过定点 $P$ ，过点 $P$ 作直线 $l$ 平行于 $x$ 轴交图象 $C_{1}$ 于另一个点 $Q$ ，点 $M$ 为点 $Q$ 关于点 $E (2 ， 0)$ 的对称点.试判断点 $M$ 是否在图象 $C_{2}$ 上？

查看试题解析
26. （阅读理解）：有一组对角互余的四边形称为对余四边形.

(1)、若四边形ABCD是对余四边形，∠A＝60°，∠B＝130°，求∠D的度数.

(2)、在四边形ABCD中，AB＝AC，∠BAC＝90°.

①如图1，点E为BC边上一点，AE＝AD，若四边形ABED为对余四边形，求证：BE＝CD；

②如图2，若BC＝ $2 \sqrt{2}$ ，CD＝ $\sqrt{2}$ ，AD＝ $\sqrt{3} + 1$ ，试判断四边形ABCD是否为对余四边形，并说明理由；

③如图2，若四边形ABCD是对余四边形，当BD＝6，AD＝4时，求CD的长.

查看试题解析

饮料品种	成本价（元/箱）	销售价（元/箱）
甲	18	24
乙	22	25