江苏省苏州市高新区2021年数学中考一模试卷
试卷更新日期:2021-06-10 类型:中考模拟
一、单选题
-
1. 下列计算结果为a6的是( )A、a2+a4 B、a2·a3 C、a6÷a D、(a2)32. 2021年3月20日,苏州高新区召开2021年一季度经济运行分析会.会议指出,1-2月,苏州高新区各项经济指标实现较快增长.进出口总额63.9亿美元,同比增长47%,其中出口41.9亿美元,同比增长64%,出口增速位居全市第1.数据41.9亿用科学记数法表示为( )A、 0.419×1010 B、4.19×109 C、41.9×108 D、4.19×1083. 在某市2021年青少年航空航天模型锦标赛中,各年龄组的参赛人数情况如下表所示:
年龄组
13岁
14岁
15岁
16岁
参赛人数
5
19
12
14
若小明所在年龄组的参赛人数占全体参赛人数的38%,则小明所在的年龄组是( )
A、13岁 B、14岁 C、15岁 D、16岁4. 如图,将一块含30°的直角三角板绕点A按顺时针方向旋转到△A1B1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )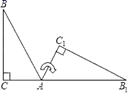 A、30° B、60° C、90° D、120°5. 下列图形中,三视图都相同的是( )A、圆柱 B、球 C、三棱锥 D、五棱柱6. 如图,直线a、b被直线c所截, , ,则 的度数是( )
A、30° B、60° C、90° D、120°5. 下列图形中,三视图都相同的是( )A、圆柱 B、球 C、三棱锥 D、五棱柱6. 如图,直线a、b被直线c所截, , ,则 的度数是( ) A、30° B、40° C、50° D、60°7. 如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )。
A、30° B、40° C、50° D、60°7. 如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )。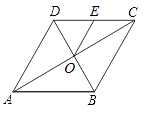 A、 B、2 C、 D、48. 图1是一个地铁站入口的双翼闸机.如图2,当双翼收起时,可以通过闸机的物体的最大宽度是64cm,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,此时双翼的边缘AC、BD与闸机侧立面夹角∠PCA=∠BDQ=30°,则双翼的边缘AC、BD(AC=BD)的长度为( )
A、 B、2 C、 D、48. 图1是一个地铁站入口的双翼闸机.如图2,当双翼收起时,可以通过闸机的物体的最大宽度是64cm,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,此时双翼的边缘AC、BD与闸机侧立面夹角∠PCA=∠BDQ=30°,则双翼的边缘AC、BD(AC=BD)的长度为( ) A、 cm B、 cm C、27cm D、54cm9. 如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法:①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.其中,一定正确的是( )
A、 cm B、 cm C、27cm D、54cm9. 如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法:①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.其中,一定正确的是( ) A、①③ B、①④ C、②④ D、③④10. 如图,点D是▱OABC内一点,AD与x轴平行,BD与y轴平行,BD= ,∠BDC=120°,S△BDC= .若反比例函数 的图象经过C、D两点,则k的值是( )
A、①③ B、①④ C、②④ D、③④10. 如图,点D是▱OABC内一点,AD与x轴平行,BD与y轴平行,BD= ,∠BDC=120°,S△BDC= .若反比例函数 的图象经过C、D两点,则k的值是( )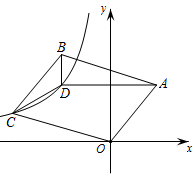 A、 B、-6 C、 D、-3
A、 B、-6 C、 D、-3二、填空题
-
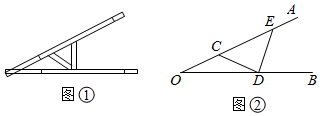
11. 的平方根是 .12. 函数y= 的自变量x的取值范围是 。13. 解不等式组 的解集为.14. 已知圆锥的底面半径为3cm,侧面积为15πcm2 , 则该圆锥的母线长为cm.15. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠CDE是 °.
 16. 在平面直角坐标系中,如果存在一点P(a,b),满足ab =-1,那么称点P为“负倒数点”,则函数 的图象上负倒数点的个数为个.17. 如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为S1 , 空白部分的面积为S2 , 大正方形的边长为m,小正方形的边长为n,若 ,则 的值为.
16. 在平面直角坐标系中,如果存在一点P(a,b),满足ab =-1,那么称点P为“负倒数点”,则函数 的图象上负倒数点的个数为个.17. 如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为S1 , 空白部分的面积为S2 , 大正方形的边长为m,小正方形的边长为n,若 ,则 的值为. 18. 如图,在边长为 的等边△ABC中,点D、点E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.连接CF,则CF的最小值为.
18. 如图,在边长为 的等边△ABC中,点D、点E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.连接CF,则CF的最小值为.
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中 .21. 如图,以点O为旋转中心,将线段AB按顺时针方向旋转 得到线段A′B′,连结AA′、BB′.
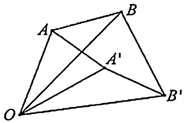 (1)、比较∠OAA′与∠OBB′的大小,并说明理由.(2)、若BB′=5,sin∠OB′B= ,求OB的长.22. “五·一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.下图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:
(1)、比较∠OAA′与∠OBB′的大小,并说明理由.(2)、若BB′=5,sin∠OB′B= ,求OB的长.22. “五·一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.下图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题: (1)、若去D地的车票占全部车票的10%,请求出D地车票的数量,并补全统计图;(2)、若公司采用随机抽取的方式分发车票,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小胡抽到去A地的概率是多少?(3)、若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否则给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?23. 某商场代理销售一种货物,四月份的销售利润y(元)与销售量x(kg)之间函数关系的图象如图中折线所示.请你根据图象及这种货物的相关销售记录提供的信息,解答下列问题:
(1)、若去D地的车票占全部车票的10%,请求出D地车票的数量,并补全统计图;(2)、若公司采用随机抽取的方式分发车票,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小胡抽到去A地的概率是多少?(3)、若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否则给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?23. 某商场代理销售一种货物,四月份的销售利润y(元)与销售量x(kg)之间函数关系的图象如图中折线所示.请你根据图象及这种货物的相关销售记录提供的信息,解答下列问题: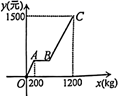 (1)、截止到4月8日,该商店销售这种货物一共获利多少元?(2)、求图象中线段BC所在直线对应的函数表达式.
(1)、截止到4月8日,该商店销售这种货物一共获利多少元?(2)、求图象中线段BC所在直线对应的函数表达式.日期
销售记录
4月1日
库存1000kg,成本价10元/kg,售价12元/kg(除了促销降价,其他时间售价保持不变).
4月8日
从4月1日至今,一共售出200kg.
4月9、10日
这两天以成本价促销,之后售价恢复到12元/kg
4月11日
补充进货200kg,成本价10.5元/kg.
4月30日
1200kg货物全部售完,一共获利1500元.
24. 如图(1)、(2)分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732, ≈1.732, ≈1.414)

 (1)、求支架AC的顶端A到地面的距离AB的高度.(精确到0.001米)(2)、求篮框D到地面的距离.(精确到0.01米)25. 如图,△ABC内接于⊙O,AD平分∠BAC交BC边于点E,交⊙O于点D,过点A作AF⊥BC于点F,设⊙O的直径为d,AF=h.
(1)、求支架AC的顶端A到地面的距离AB的高度.(精确到0.001米)(2)、求篮框D到地面的距离.(精确到0.01米)25. 如图,△ABC内接于⊙O,AD平分∠BAC交BC边于点E,交⊙O于点D,过点A作AF⊥BC于点F,设⊙O的直径为d,AF=h. (1)、过点D作直线MN∥BC,求证:MN是⊙O的切线;(2)、若AB=4,AC=3,求dh的值.26. 为庆祝五四青年节,某校九年级(1)班将举行班级联欢活动,决定到水果店购买A、B两种水果,据了解,购买A种水果3千克,B种水果4千克,则需180元;购买A种水果2千克,B种水果8千克,则需280元.(1)、求A、B两种水果的单价分别是多少元?(2)、经初步测算班级联欢活动需要购买A、B两种水果10千克,但九年级班委会目前只有班级经费230元,则A种水果至少需要购买多少千克?(3)、考虑到实际情况,经九年级(1)班班委会商定,决定购买A、B两种水果共12千克供同学们食用.水果店销售人员为了支持本次活动,为该班同学提供以下优惠:购买多少千克B种水果,B种水果每千克就降价多少元,请你为九年级(1)班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?27. 定义:若一个三角形存在两个内角之差是第三个内角的两倍,则称这个三角形为关于第三个内角的“差倍角三角形”,例如,在△ABC中,∠A=100°,∠B=60°,∠C=20°,满足∠A-∠B=2∠C,所以△ABC是关于∠C的“差倍角三角形”;
(1)、过点D作直线MN∥BC,求证:MN是⊙O的切线;(2)、若AB=4,AC=3,求dh的值.26. 为庆祝五四青年节,某校九年级(1)班将举行班级联欢活动,决定到水果店购买A、B两种水果,据了解,购买A种水果3千克,B种水果4千克,则需180元;购买A种水果2千克,B种水果8千克,则需280元.(1)、求A、B两种水果的单价分别是多少元?(2)、经初步测算班级联欢活动需要购买A、B两种水果10千克,但九年级班委会目前只有班级经费230元,则A种水果至少需要购买多少千克?(3)、考虑到实际情况,经九年级(1)班班委会商定,决定购买A、B两种水果共12千克供同学们食用.水果店销售人员为了支持本次活动,为该班同学提供以下优惠:购买多少千克B种水果,B种水果每千克就降价多少元,请你为九年级(1)班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?27. 定义:若一个三角形存在两个内角之差是第三个内角的两倍,则称这个三角形为关于第三个内角的“差倍角三角形”,例如,在△ABC中,∠A=100°,∠B=60°,∠C=20°,满足∠A-∠B=2∠C,所以△ABC是关于∠C的“差倍角三角形”;

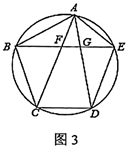 (1)、如图1,△ABC是关于∠C的“差倍角三角形”(其中∠BAC>∠B),AB=3,BC=9,点D在BC上,且∠BAD=∠C.求AC的长.(2)、如图2,等腰三角形ABC中,点D是底边BC的一个黄金分割点(CD<BD),且AB=AC=BD.求证:△ABC是关于∠B的“差倍角三角形”.(3)、如图3,五边形ABCDE内接于圆,连接AC,AD与BE相交于点F,G,BF=1,AB=BC=DE,△ABE是关于∠AEB的“差倍角三角形”.设AB=x,CD=y,求y关于x的函数关系式.28. 如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=8.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)、如图1,△ABC是关于∠C的“差倍角三角形”(其中∠BAC>∠B),AB=3,BC=9,点D在BC上,且∠BAD=∠C.求AC的长.(2)、如图2,等腰三角形ABC中,点D是底边BC的一个黄金分割点(CD<BD),且AB=AC=BD.求证:△ABC是关于∠B的“差倍角三角形”.(3)、如图3,五边形ABCDE内接于圆,连接AC,AD与BE相交于点F,G,BF=1,AB=BC=DE,△ABE是关于∠AEB的“差倍角三角形”.设AB=x,CD=y,求y关于x的函数关系式.28. 如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=8.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.

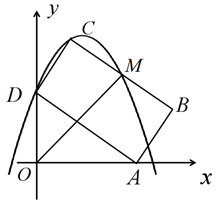 (1)、当∠OAD=30°时,求点C的坐标;(2)、设BC的中点为M,连接OM.
(1)、当∠OAD=30°时,求点C的坐标;(2)、设BC的中点为M,连接OM.①探究:在点A移动的过程中,∠MOA的度数是否会发生变化?若发生变化,请求出∠MOA度数的取值范围;若不发生变化,请求出∠MOA的度数;
②当OM取最大值时,设过点D、C、M三点的抛物线与直线AB交于点N,请求出点N的坐标.