江苏省南京市八区联合体2021年数学中考一模试卷

试卷更新日期：2021-06-10 类型：中考模拟

进入 出卷网 下载

一、单选题

  • 1. 比－2小的数是（   ）
    A、－3 B、－1 C、0 D、1

    查看试题解析

  • 2. 下列运算正确的是（   ）
    A、a3＋a3＝a6 B、a2·a3＝a6 C、a6÷a2＝a4 D、（a3）2＝a9

    查看试题解析

  • 3. 当x＝1时，下列式子没有意义的是（   ）
    A、xx+1 B、x−1x C、x−1 D、xx−1

    查看试题解析

  • 4. 如图，数轴上两点M、N所对应的实数分别为m、n，则m－n的结果可能为（   ）

    A、4 B、3 C、2 D、－0.3

    查看试题解析

  • 5. 如图，在△ABC中，∠C＝90°，沿DE翻折使得A与B重合，∠CBD＝26°，则∠ADE的度数是（   ）

    A、57° B、58° C、59° D、60°

    查看试题解析

  • 6. 关于x的方程px2＋p＝ qx （p、q为常数，且pq≠0）的根的情况，下列结论中正确的是（   ）
    A、一个根 B、二个根 C、三个根 D、无实数根

    查看试题解析

二、填空题

  • 7. 5的平方根为 ， 5的算术平方根为.

    查看试题解析

  • 8. 华为正在研制厚度为0.000 000 005m的芯片.用科学记数法表示0.000 000 005是.

    查看试题解析

  • 9. 计算 3 ×（ 12 － 3 ）的结果是 .

    查看试题解析

  • 10. 若x2－4x－7＝0的两个根为x1、x2 ， 则x1＋x2－x1x2的值是.

    查看试题解析

  • 11. 如图①，一个长为2a，宽为2b的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块全等的小长方形，然后按照图②那样拼成一个面积为49的大正方形，若中间小正方形的面积为1，则a＝、b＝.

    查看试题解析

  • 12. 光明中学全体学生参加社会实践活动，从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图，则这50人的社会实践活动成绩的中位数是.

    查看试题解析

  • 13. 若点A与点B（1，1）关于点C（－1，－1）对称，则点A的坐标是.

    查看试题解析

  • 14. 笔记本4元/本，钢笔5元/支，某同学购买笔记本和钢笔恰好用去162元，那么最多购买钢笔支.

    查看试题解析

  • 15. 如图，P是⊙O外一点，PB、PC是⊙O的两条切线，切点分别为B、C，若∠P为38°，点A在⊙O上（不与B、C重合），则∠BAC＝°.

    查看试题解析

  • 16. 如图，在边长为2 cm的正方形ABCD中，直线l经过点D，作BE⊥l，垂足为E，连接AE.若AE＝BE，则△ABE的面积为cm2.

    查看试题解析

三、解答题

  • 17. 计算 (1+a+2a) ÷ a2−1a .

    查看试题解析

  • 18. 解不等式组 {1−x≤0x−2<3 ，并写出不等式组的整数解.

    查看试题解析

  • 19. 如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F.

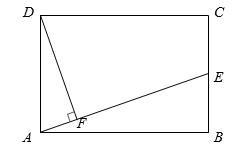    (1)、求证△ADF∽△EAB；
    (2)、若AB＝12，BC＝10，求DF的长.

    查看试题解析

  • 20. 某商场统计了A、B两种品牌洗衣机7个月的销售情况，结果如下：

    一月

    二月

    三月

    四月

    五月

    六月

    七月

    A品牌

    16

    31

    29

    24

    24

    24

    20

    B品牌

    16

    20

    24

    25

    26

    27

    30
    (1)、分别求这7个月A、B两种品牌洗衣机销量的方差；
    (2)、由于库存不足，商场采购部欲从厂家采购A、B两种品牌洗衣机以满足市场需求.请你结合上述两种品牌洗衣机的销售情况，对商场采购部提出建议，并从两个不同角度说明理由.

    查看试题解析

  • 21. 甲、乙、丙互相传球.假设他们相互之间传球是等可能的，并且由甲开始传球.
    (1)、经过2次传球后，求球仍回到甲手中的概率；
    (2)、经过3次传球后，球仍回到甲手中的概率为.

    查看试题解析

  • 22. 如图，在▱ABCD中，E、F分别为AD、BC的中点，点M、N在对角线AC上，且AM＝CN.

    (1)、求证四边形EMFN是平行四边形；
    (2)、若AB⊥AC，求证 ▱ EMFN是菱形.

    查看试题解析

  • 23. 为了测量悬停在空中A处的无人机的高度，小明在楼顶B处测得无人机的仰角为45°，小丽在地面C处测得A、B的仰角分别为56°、14°.楼高BD为20米，求此时无人机离地面的高度.（参考数据：tan14°≈0.25，tan56°≈1.50）

    查看试题解析

  • 24. 如图，在菱形ABCD中，E是CD上一点，且∠CAE＝∠B，⊙O经过点A、C、E.

    (1)、求证AC＝AE；
    (2)、求证AB与⊙O相切.

    查看试题解析

  • 25. 2020年江苏开通了多条省内高铁，其中一条可以从南京——镇江——扬州——淮安的高铁线路如图①所示，本线路高铁最高速度不超过每分钟5千米.现有甲、乙两车按以下方式营运，甲车从南京匀速行驶去淮安，在镇江和扬州两站都停靠5分钟；乙车从南京匀速行驶直达淮安，乙车比甲车晚出发20分钟.设甲车出发x分钟后行驶的路程为y1千米，图②中的折线O—A—B—C—D—E表示在整个行驶过程中y1与x的函数图象.

    (1)、甲车速度为千米/分；
    (2)、若乙车行驶1小时到达淮安，则乙车出发多久后与甲车相遇？
    (3)、若乙车行驶的过程中不得与甲车在镇江站与扬州站的站台内相遇，并要在甲之前到达淮安，则乙车速度v乙的范围为.

    查看试题解析

  • 26. 已知二次函数y＝mx2－2（m＋1）x＋4（m为常数，且m≠0）.
    (1)、求证：不论m为何值，该函数的图象与x轴总有公共点；
    (2)、不论m为何值，该函数的图象都会经过两个定点，这两个定点的坐标分别为；
    (3)、该函数图象所经过的象限随m值的变化而变化，直接写出函数图象所经过的象限及对应的m的取值范围.

    查看试题解析

  • 27. 如图，在△ABC中，∠ACB＝90°.用直尺与圆规分别作出满足下列条件的⊙O.（不写作法，保留作图痕迹）

    (1)、在图①中，⊙O过点C且与AB相切；（作出一个即可）
    (2)、在图②中，D为AB上一定点，⊙O过点C且与AB相切于点D；
    (3)、在图③中，E为AC上一定点，⊙O过点C、E且与AB相切.

    查看试题解析