湖北省黄冈市2021年数学中考模拟试卷(3月)
试卷更新日期:2021-06-10 类型:中考模拟
一、单选题
-
1. 与-3互为相反数的是( )A、-3 B、3 C、- D、2. 下列运算中,正确的是( )A、 B、 C、 D、3. 已知,如图, ,则 、 、 之间的关系为( )
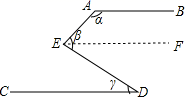 A、 B、 C、 D、4. 如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是( )
A、 B、 C、 D、4. 如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是( ) A、72° B、60° C、54° D、36°5. 下面几个几何体,从正面看到的形状是圆的是( )A、
A、72° B、60° C、54° D、36°5. 下面几个几何体,从正面看到的形状是圆的是( )A、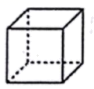 B、
B、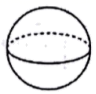 C、
C、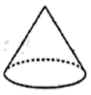 D、
D、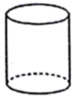 6. 如果关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 且 D、 且7. 对于两组数据A,B,如果 ,且 ,则( )A、这两组数据的波动相同 B、数据B的波动小一些 C、它们的平均水平不相同 D、数据A的波动小一些8. 如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )
6. 如果关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 且 D、 且7. 对于两组数据A,B,如果 ,且 ,则( )A、这两组数据的波动相同 B、数据B的波动小一些 C、它们的平均水平不相同 D、数据A的波动小一些8. 如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为( )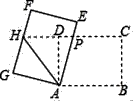 A、15 B、18 C、20 D、24
A、15 B、18 C、20 D、24二、填空题
-
9. 计算:(1)、 ;(2)、 .10. 自然界中,花粉的质量很小,一粒某种植物花粉的质量约为0.000042毫克,0.000042用科学记数法表示为.11. 若 在实数范围内有意义,则x的取值范围是 .12. 如图,已知直线 与双曲线 交于A,B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落在点C处,双曲线 经过点C,则 的值是.
 13. 如图所示为一弯形管道,其中心线是一段圆弧 .已知半径OA=60cm,∠AOB=108°,则管道的长度(即 的长)为cm.(结果保留π)
13. 如图所示为一弯形管道,其中心线是一段圆弧 .已知半径OA=60cm,∠AOB=108°,则管道的长度(即 的长)为cm.(结果保留π) 14. 如果乘坐出租车所付款金额 (元)与乘坐距离 (千米)之间的函数图象由线段 、线段 和射线 组成(如图所示),那么乘坐该出租车8(千米)需要支付的金额为元.
14. 如果乘坐出租车所付款金额 (元)与乘坐距离 (千米)之间的函数图象由线段 、线段 和射线 组成(如图所示),那么乘坐该出租车8(千米)需要支付的金额为元.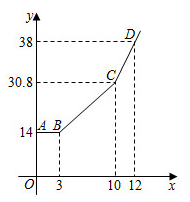 15. 如图, 是 的直径, ,点C在 上, ,D为 的中点,P是直径 上一动点,则 的最小值为.
15. 如图, 是 的直径, ,点C在 上, ,D为 的中点,P是直径 上一动点,则 的最小值为.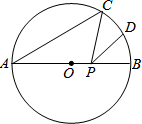 16.
16.如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为

三、解答题
-
17. 计算: .18. 解分式方程 = ﹣2圆圆的解答如下:
解:去分母,得1﹣x=﹣1﹣2化简,得x=4经检验,x=4是原方程的解.
∴原方程的解为x=4.
圆圆的解答正确吗?如果不正确,写出正确的解答.
19. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ. (1)、如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;(2)、如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).20. 某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:(1)、求出足球和篮球的单价;(2)、若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?(3)、在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?21. 中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”,针对这种现象某媒体记者在多个路口采访闯红灯的行人,得出形成这种现象的四个基本原因:①马路红灯时间长,交通管理混乱占2%;②侥幸心态,只图自己节省时间;③对行人闯红灯违规行为惩罚措施不够严厉占8%;④从众心理.该记者将这次调查情况整理并绘制了如图尚不完整的统计图,请根据相关信息,解答下列问题.
(1)、如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;(2)、如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).20. 某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:(1)、求出足球和篮球的单价;(2)、若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?(3)、在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?21. 中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”,针对这种现象某媒体记者在多个路口采访闯红灯的行人,得出形成这种现象的四个基本原因:①马路红灯时间长,交通管理混乱占2%;②侥幸心态,只图自己节省时间;③对行人闯红灯违规行为惩罚措施不够严厉占8%;④从众心理.该记者将这次调查情况整理并绘制了如图尚不完整的统计图,请根据相关信息,解答下列问题.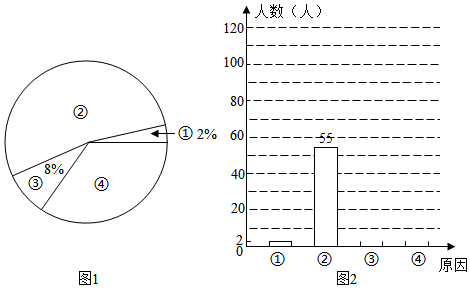 (1)、该记者本次一共调查了名行人;(2)、求图1中②所在扇形的圆心角度数,并补全图2;(3)、在本次调查中,记者随机采访其中的一名行人,求这名行人属于第④种情况的概率.22. 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
(1)、该记者本次一共调查了名行人;(2)、求图1中②所在扇形的圆心角度数,并补全图2;(3)、在本次调查中,记者随机采访其中的一名行人,求这名行人属于第④种情况的概率.22. 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.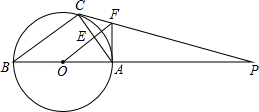 (1)、判断AF与⊙O的位置关系并说明理由;(2)、若⊙O的半径为4,AF=3,求AC的长.23. 郑州市农业路高架桥二层的开通,较大程度缓解了市内交通的压力,最初设计南阳路口上桥匝道时,其坡角为15°,后来从安全角度考虑将匝道坡角改为5°(见示意图),如果高架桥高CD=6米,匝道BD和AD每米造价均为4 000元,那么设计优化后修建匝道AD的投资将增加多少元?(参考数据:sin5°≈0.08,sin15°≈0.25,tan5°≈0.09,tan15°≈0.27,结果保留整数)
(1)、判断AF与⊙O的位置关系并说明理由;(2)、若⊙O的半径为4,AF=3,求AC的长.23. 郑州市农业路高架桥二层的开通,较大程度缓解了市内交通的压力,最初设计南阳路口上桥匝道时,其坡角为15°,后来从安全角度考虑将匝道坡角改为5°(见示意图),如果高架桥高CD=6米,匝道BD和AD每米造价均为4 000元,那么设计优化后修建匝道AD的投资将增加多少元?(参考数据:sin5°≈0.08,sin15°≈0.25,tan5°≈0.09,tan15°≈0.27,结果保留整数)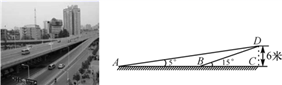 24. 小明参加实心球测试,某次投掷中实心球所经过的路线为二次函数图象的一部分(单位:米),该函数解析式为 .(1)、直接写出小明出手时实心球的高度是多少米?(2)、实心球在运行中离地面的最大高度是多少米?(3)、如果实心球评分标准中规定10米及以上为优秀成绩,那么小明在这次测试中成绩是否能达到优秀?请说明理由.25. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
24. 小明参加实心球测试,某次投掷中实心球所经过的路线为二次函数图象的一部分(单位:米),该函数解析式为 .(1)、直接写出小明出手时实心球的高度是多少米?(2)、实心球在运行中离地面的最大高度是多少米?(3)、如果实心球评分标准中规定10米及以上为优秀成绩,那么小明在这次测试中成绩是否能达到优秀?请说明理由.25. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D. (1)、抛物线及直线AC的函数关系式;(2)、若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(3)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
(1)、抛物线及直线AC的函数关系式;(2)、若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(3)、若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.