福建省百校联合2021年数学中考一模试卷
试卷更新日期:2021-06-10 类型:中考模拟
一、单选题
-
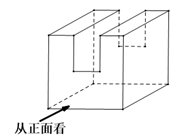
1. 的相反数是( )A、3 B、-3 C、 D、2. 据报道,研究人员通过研究获得了纯化灭活新冠病毒疫苗,该疫苗在低温电镜下呈椭圆形颗粒,最小直径约为 ,已经 ,则 用科学记数法表示为( )A、 B、 C、 D、3. 下列算式运算结果为 的是( )A、 B、 C、 D、4. 如图是某几何体放置在水平面上,则其俯视图是( )
 A、
A、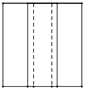 B、
B、 C、
C、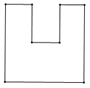 D、
D、 5. 现有一组数据:2,3,3,4,4,5,6,则下列说法正确的是( )A、众数是3 B、众数是4 C、中位数是3.5 D、中位数是46. 若要说明命题“若 ,则 ”不正确,则可以列举的反例是( )A、 , B、 , C、 , D、 ,7. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( )
5. 现有一组数据:2,3,3,4,4,5,6,则下列说法正确的是( )A、众数是3 B、众数是4 C、中位数是3.5 D、中位数是46. 若要说明命题“若 ,则 ”不正确,则可以列举的反例是( )A、 , B、 , C、 , D、 ,7. 如图,在 中,点 , , 分别在 , , 边上, , ,则下列式子一定正确的是( ) A、 B、 C、 D、8. 如图,在 中,半径 ,点 是优弧 上的一点,点 是 的中点,连接 , ,则 的度数为( )
A、 B、 C、 D、8. 如图,在 中,半径 ,点 是优弧 上的一点,点 是 的中点,连接 , ,则 的度数为( ) A、20° B、22.5° C、25° D、45°9. 《九章算术》有题如下:“仅有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”意思是:今有5只雀、6只燕,分别聚集而用衡器称之,聚在一起的雀重、燕轻,将1只雀、1只燕交换位置而放,重量相同.5只雀、6只燕重量为1斤.问燕雀每只各重多少?(注:古代1斤=16两)若设每只雀、燕分别重 两、 两,则可列方程组为( )A、 B、 C、 D、10. 定义:当关于 的一元二次方程 满足 时,称此方程为“合理”方程.若“合理”方程 有两个相等的实数根,则下列等式正确的是( )A、 B、 C、 D、
A、20° B、22.5° C、25° D、45°9. 《九章算术》有题如下:“仅有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”意思是:今有5只雀、6只燕,分别聚集而用衡器称之,聚在一起的雀重、燕轻,将1只雀、1只燕交换位置而放,重量相同.5只雀、6只燕重量为1斤.问燕雀每只各重多少?(注:古代1斤=16两)若设每只雀、燕分别重 两、 两,则可列方程组为( )A、 B、 C、 D、10. 定义:当关于 的一元二次方程 满足 时,称此方程为“合理”方程.若“合理”方程 有两个相等的实数根,则下列等式正确的是( )A、 B、 C、 D、二、填空题
-
11. .12. 若某斜面的坡度为 ,则该坡面的坡角为.13. 若一个半径为5的扇形的弧长为 ,则该扇形的面积为.14. 如图,其中的 和 是由 分别沿着直线 , 折叠得到的, 与 相交于点 ,若 ,则 °.
 15. 在菱形 中,对角线 与 相交于点 , , ,则菱形 的内切圆半径为.
15. 在菱形 中,对角线 与 相交于点 , , ,则菱形 的内切圆半径为.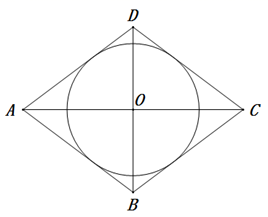 16. 如图,矩形 的顶点 , , , 分别在反比例函数 和 ( , )的图象上,点 的坐标为 , ,若矩形 的对称轴经过点 ,则 .
16. 如图,矩形 的顶点 , , , 分别在反比例函数 和 ( , )的图象上,点 的坐标为 , ,若矩形 的对称轴经过点 ,则 .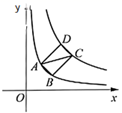
三、解答题
-
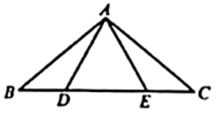
17. 解不等式组:18. 先化简,再求值: ,其中 .19. 如图,在等腰三角形 中, ,点 , 在 边上, .求证: .
 20. 如图,将两块完全相同的含30°角的直角三角尺的斜边叠合,可得矩形 , , ,将 沿水平方向向左平移,使得点 恰好为边 的中点, 与 相交于点 , 与 相交于点 , .求重重叠部分四边形 的面积.
20. 如图,将两块完全相同的含30°角的直角三角尺的斜边叠合,可得矩形 , , ,将 沿水平方向向左平移,使得点 恰好为边 的中点, 与 相交于点 , 与 相交于点 , .求重重叠部分四边形 的面积.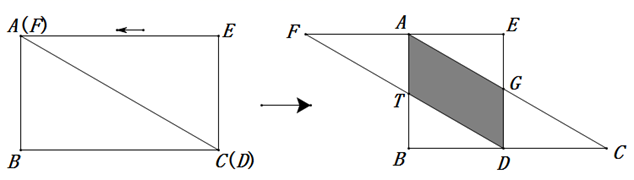 21. 如图,将 绕点 按逆时针方向旋转 的度数得到 .
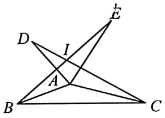
21. 如图,将 绕点 按逆时针方向旋转 的度数得到 .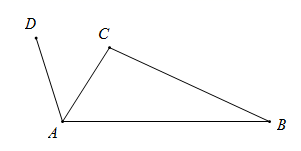 (1)、尺规作图:确定 的顶点 的位置(保留作图痕迹,不写作法与证明过程);(2)、连接 , ,设 的延长线交 于点 ,连接 .求证: 平分 .22. 国庆期间,为了满足群众的消费需求,某电器商场计划用190000元购进一批家电,这批家电的进价和售价如下表:
(1)、尺规作图:确定 的顶点 的位置(保留作图痕迹,不写作法与证明过程);(2)、连接 , ,设 的延长线交 于点 ,连接 .求证: 平分 .22. 国庆期间,为了满足群众的消费需求,某电器商场计划用190000元购进一批家电,这批家电的进价和售价如下表:类别
彩电
冰箱
洗衣机
进价(元/台)
2000
1400
1000
售价(元/台)
2400
1600
1100
若在现有资金允许的范围内,购买上表中三类家电共100台,其中彩电台数是洗衣机台数的2倍,设该电器商场购买洗衣机 台.
(1)、电器商场至多可以购买洗衣机多少台?(2)、购买洗衣机多少台时,能使电器商场销售完这批家电后获得的利润最大?最大利润为多少元?23. 某超市开展“五一”大酬宾,举行购物抽奖活动,奖项设置为面值不同的购物卡,分别是:一等奖120元,二等奖60元,三等奖10元,凡购买满200元及以上者,每200元可抽奖一次(不足200元一概不计入,每人当天购物最多可抽5次),每次抽奖过程如下:在一个不透明的袋子里装有三个小球,球面上分别标注数字“1”,“2”,“3”,它们除数字不同外没有任何区别.抽奖顾客先随机摸出一球,记下数字后,将小球放回袋中充分搅匀,再随机摸出一球,若两球标注的数字之和为6,则获一等奖,数字之和为5,则获二等奖,数字之和为4,则获三等奖,其余均不获奖.(1)、试利用树状图或列表法顾客每抽奖一次分别获得一等奖、二等奖、三等奖的概率;(2)、若此次超市大酬宾中,超市业绩调查部分随机抽查了100位顾客的消费金额并绘制成条形统计图如下(金额折算为200元的整数倍,其中扣除200元的整数倍后不足200元的部分全部去掉不计入):
①求上述样本数据中每位顾客消费金额的平均数;
②据“五一节”当天统计,共有2500位顾客参与该超市的购物抽奖活动,已知该超市每销售100元,平均可获利20元,请根据上述样本数据分析,扣除兑现的购物卡金融外,估计这一天超市共盈利大约为多少元?
24. 如图1, 是 的外接圆,点 是 的中点,过点 作 ,交弦 的延长线于点 .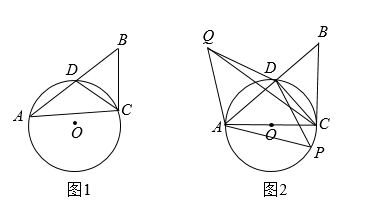 (1)、求证: ;(2)、若 的半径为6,求 的值;(3)、如图2,若 是半圆,点 是 上的动点,且点 , 分别位于 的两侧,作 关于 的轴对称图形 ,连接 ,试探究 , , 三者之间满足的数量关系,并证明所得到的结论.25. 如图,将边长为8的正方形 放置在平面直角坐标系中, 为坐标原点,点 在第二象限,点 的坐标为 ,点 在 边上的运动,连接 ,取 的中点 ,将 绕点 逆时针旋转90°得到线段 ,顶点为 的抛物线 经过原点 .当 时,
(1)、求证: ;(2)、若 的半径为6,求 的值;(3)、如图2,若 是半圆,点 是 上的动点,且点 , 分别位于 的两侧,作 关于 的轴对称图形 ,连接 ,试探究 , , 三者之间满足的数量关系,并证明所得到的结论.25. 如图,将边长为8的正方形 放置在平面直角坐标系中, 为坐标原点,点 在第二象限,点 的坐标为 ,点 在 边上的运动,连接 ,取 的中点 ,将 绕点 逆时针旋转90°得到线段 ,顶点为 的抛物线 经过原点 .当 时,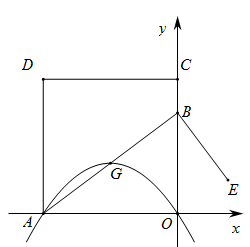 (1)、求点 的坐标;(2)、在抛物线 上是否存在点 ,使得 与 互余?若存在,求出点 的坐标,若不存在,请说明理由;
(1)、求点 的坐标;(2)、在抛物线 上是否存在点 ,使得 与 互余?若存在,求出点 的坐标,若不存在,请说明理由;