江苏省无锡市江阴市青阳片2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-06-10 类型:期中考试
一、单选题
-
1. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、
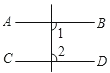 B、
B、 C、
C、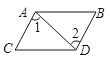 D、
D、 2. 下列各网格中的图形是用其图形中的一部分平移得到的是( )A、
2. 下列各网格中的图形是用其图形中的一部分平移得到的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、a2+a3=a5 B、a·a2=a2 C、(ab)3=ab3 D、(-a2)2=a44. 如图,已知 ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2的和的度数为( )
3. 下列计算正确的是( )A、a2+a3=a5 B、a·a2=a2 C、(ab)3=ab3 D、(-a2)2=a44. 如图,已知 ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2的和的度数为( ) A、220° B、210° C、140° D、120°5. 如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=( )
A、220° B、210° C、140° D、120°5. 如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=( ) A、50° B、40° C、70° D、35°6. 如图,∠ACB>90°,AD^BC,BE^AC,CF^AB,垂足分别为点D、点E、点F, ABC中BC边上的高是( )
A、50° B、40° C、70° D、35°6. 如图,∠ACB>90°,AD^BC,BE^AC,CF^AB,垂足分别为点D、点E、点F, ABC中BC边上的高是( ) A、CF B、BE C、AD D、CD7. 如果 , ,那么 三数的大小为( )A、 B、 C、 D、8. 若 ,则( )A、 , B、 , C、 , D、 ,9. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为5、6、7,四边形DHOG面积为( )
A、CF B、BE C、AD D、CD7. 如果 , ,那么 三数的大小为( )A、 B、 C、 D、8. 若 ,则( )A、 , B、 , C、 , D、 ,9. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为5、6、7,四边形DHOG面积为( ) A、5 B、6 C、8 D、910. 观察下列等式:
A、5 B、6 C、8 D、910. 观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…
解答下列问题:3+32+33+34…+32013的末位数字是( )
A、0 B、1 C、3 D、7二、填空题
-
11. 一种细菌的半径是0.00000038厘米,用科学记数法表示为厘米.12. 若 则 .若 ,则 .13. 二次三项式 是一个完全平方式,则 的值是.14. 一个多边形的每一个外角等于 ,则这个多边形是边形,其内角和是 .15. 三角形两边长分别为2和8,若该三角形第三边长为奇数,则该三角形的第三边为.16. 如图,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图,画 ,量出直线b与PC的夹角度数,即直线a,b所成角的度数,请写出这种做法的理由.
 17. 已知m2+m﹣1=0,则m3+2m2+2014=.18. 如图a是长方形纸带,∠DEF=22°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是°.
17. 已知m2+m﹣1=0,则m3+2m2+2014=.18. 如图a是长方形纸带,∠DEF=22°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是°. 19. 利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.你能利用数形结合的思想解决下列问题吗?(1)、如图①,一个边长为1的正方形,依次取正方形面积的 、 、 、…、 ,根据图示我们可以知道: + + + +…+ = . (用含有n的式子表示)
19. 利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.你能利用数形结合的思想解决下列问题吗?(1)、如图①,一个边长为1的正方形,依次取正方形面积的 、 、 、…、 ,根据图示我们可以知道: + + + +…+ = . (用含有n的式子表示) (2)、如图②,一个边长为1的正方形,依次取剩余部分的 ,根据图示:
(2)、如图②,一个边长为1的正方形,依次取剩余部分的 ,根据图示:计算: + + +…+ = . (用含有n的式子表示)
 (3)、如图③是一个边长为1的正方形,根据图示:
(3)、如图③是一个边长为1的正方形,根据图示:
计算: + + + +…+ = . (用含有n的式子表示)
三、解答题
-
20. 计算(1)、(2)、(3)、−x(2x+1)−(2x+3)(1−x)(4)、(x+1)2﹣(x+2)(x-2)21. 先化简,再求值: ,其中22. 如图,在每个小正方形边长为1的方格纸中, ABC的顶点都在方格纸格点上.
 (1)、将 ABC经过平移后得到 ,图中标出了点B的对应点 ,补全 ;(2)、若连接 , ,则这两条线段之间的关系是;(3)、画出AC边上的高线BD;(4)、画出 ABC中AC边上的中线BE;(5)、 BCE的面积为.23. 如图,AD∥BE , AE平分∠BAD , CD与AE相交于F , ∠CFE=∠E . 求证:AB∥CD .
(1)、将 ABC经过平移后得到 ,图中标出了点B的对应点 ,补全 ;(2)、若连接 , ,则这两条线段之间的关系是;(3)、画出AC边上的高线BD;(4)、画出 ABC中AC边上的中线BE;(5)、 BCE的面积为.23. 如图,AD∥BE , AE平分∠BAD , CD与AE相交于F , ∠CFE=∠E . 求证:AB∥CD . 24. 如图,DE⊥AB,EF∥AC,∠A=32°,
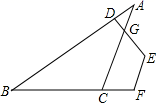
24. 如图,DE⊥AB,EF∥AC,∠A=32°,①求∠DEF的度数;
②若∠F比∠ACF大60°,求∠B的度数.
 25. 某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
25. 某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合). (1)、在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐;连接FC,∠FCE的度数逐渐.(填“不变”、“变大”或“变小”)(2)、△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;(3)、能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.26. 如图,已知点A、B分别在∠MON的边ON、OM上(不与点O重合),AD平分∠BAN,BC平分∠ABM,直线AD,BC相交于点C.
(1)、在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐;连接FC,∠FCE的度数逐渐.(填“不变”、“变大”或“变小”)(2)、△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;(3)、能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.26. 如图,已知点A、B分别在∠MON的边ON、OM上(不与点O重合),AD平分∠BAN,BC平分∠ABM,直线AD,BC相交于点C. (1)、如图1,若∠MON = 90°,试猜想∠ACB= °;(2)、如图2,在(1)的基础上,若∠MON每秒钟变小10°,经过了t秒(0 <t < 9),
(1)、如图1,若∠MON = 90°,试猜想∠ACB= °;(2)、如图2,在(1)的基础上,若∠MON每秒钟变小10°,经过了t秒(0 <t < 9),①试用含t的代数式表示∠ACB的度数;
②并求出当t取何值时,∠MON与∠ACB的度数相等;
(3)、如图3,在(2)的条件下,若BC平分∠ABO,其它条件不改变,请直接写出∠BCD与∠MON的关系.