江苏省连云港市赣榆区2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-06-10 类型:期中考试
一、单选题
-
1. 一种病毒的长度约为0.000000432毫米,数据0.000000432用科学记数法表示为( )A、432×10﹣8 B、4.32×10﹣7 C、4.32×10﹣6 D、0.432×10﹣52. 下列计算正确的是( )A、 B、 C、 D、3. 如果一个多边形的内角和等于720°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形4. 下列由左到右的变形中属于因式分解的是( )A、 B、 C、 D、5. 若 是完全平方式,则a等于( )A、4 B、8 C、 D、6. 如图,直线 ,直线 与 、 分别交于A、B两点,点C是直线 上一点,且AC⊥AB,若∠1=42°,则 的度数是( )
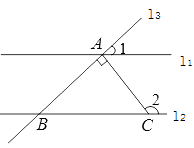 A、142° B、138° C、132° D、48°7. 将一副直角三角板如图所示放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边在同一条直线上,则 的度数为( )
A、142° B、138° C、132° D、48°7. 将一副直角三角板如图所示放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边在同一条直线上,则 的度数为( )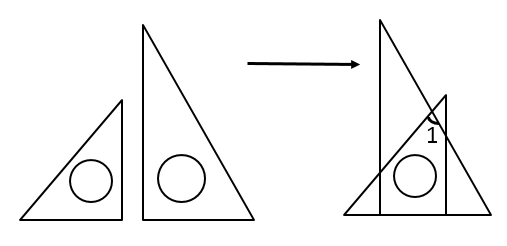 A、 B、 C、 D、8. 如图,已知D、E分别是 边AB,BC上的点, ,设 的面积为 , 的面积为 ,若 ,则 的值为( )
A、 B、 C、 D、8. 如图,已知D、E分别是 边AB,BC上的点, ,设 的面积为 , 的面积为 ,若 ,则 的值为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
9. .10. 分解因式:x2﹣64=.11. 已知 ,则 的值等于.12. 若 中不含 的一次项,则 的值为13. 若(2a﹣3b)2=(2a+3b)2+N,则表示N的代数式是 .14. 如图,△ABC中,DE∥BC,将△ADE沿DE翻折,使得点A落在平面内的A′处,若∠B=50°,则∠BDA′的度数是.
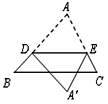 15. 如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于度.
15. 如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于度. 16. 图,直线 ,直线l与直线AB,CD相交于点E、F,点P是射线EA上的一个动点(不包括端点E),将 沿PF折叠,使顶点E落在点Q处.若∠PEF=75°,2∠CFQ=∠PFC,则 .
16. 图,直线 ,直线l与直线AB,CD相交于点E、F,点P是射线EA上的一个动点(不包括端点E),将 沿PF折叠,使顶点E落在点Q处.若∠PEF=75°,2∠CFQ=∠PFC,则 .
三、解答题
-
17. 计算和化简:(1)、(2)、18. 先化简,再求值。
(其中 )
19. 因式分解:(1)、(2)、(3)、(4)、 .20.(1)、若 求 的值;(2)、若 ,则将 用含 的代数式表示.21. 如图每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
( 1 )画出 的AB边上的中线CD;
( 2 )画出 向右平移4个单位后得到的 ;
( 3 )图中AC与 的关系是:_▲_;
( 4 )图中 的面积是_▲_;
( 5 )在现有的网格中, 与 的面积相等的格点Q共有_▲_一个.(点Q异于C)
22. 如图,BE是△ABC的角平分线,点D是AB边上一点,且∠DEB=∠DBE. (1)、DE与BC平行吗?为什么?(2)、若∠A=40°,∠ADE=60°,求∠C的度数.23. 如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
(1)、DE与BC平行吗?为什么?(2)、若∠A=40°,∠ADE=60°,求∠C的度数.23. 如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?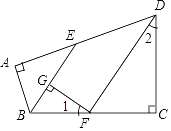 24. 对于任意有理数a、b、c、d,我们规定符号 , , ,
24. 对于任意有理数a、b、c、d,我们规定符号 , , ,例如: , , .
(1)、求 , , 的值为;(2)、求 , , 的值,其中 .25. 阅读思考:定义:把一个式子或一个式子的部分改写成完全平方式或者几个完全平方式的和的形式,这种解题方法叫配方法.
用途:配方法是初中数学一种很重要的变形技巧,是初中数学很重要的一种思想方法,应用很广泛,应用它可以简捷地处理一些解方程、因式分解、化简二次根式、证明恒等式、求代数式的最值问题.
方法:下面用拼图的方法来体会配方的过程.
例如:将代数式 (即 )写成 的形式(其中h、k为常数),配方的过程中,可以看成将一个长是 、宽是x的矩形割补成一个正方形.







所以,
(1)、模仿:用拼图的方法将式子 写成 的形式(其中h、k为常数).(2)、总结:在配方过程中,代数式需要先加上 , 再减去这个数或者代数式;(3)、应用:① ;②已知 ,求 的值.
26. 已知:在 中, .
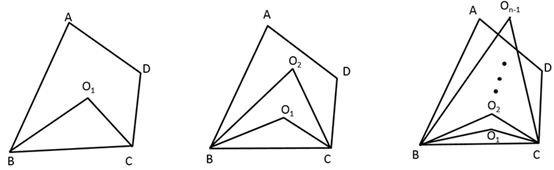 (1)、
(1)、(探究)①在左图中,设 、 的两条三等分角线分别对应交于 、 ,请你计算出 的度数;
②请你猜想,当/ 、 同时被n等分时, 条等分角线分别对应交于 、 … ,如右图,则 (用含n和a的代数式表示).

 (2)、(拓展)如图,在四边形ABCD中, ,当 、 同时被n等分时, 条等分角线分别对应交于 、 … ,如图,则 的度数是.(3)、
(2)、(拓展)如图,在四边形ABCD中, ,当 、 同时被n等分时, 条等分角线分别对应交于 、 … ,如图,则 的度数是.(3)、(感知)在图中 、 的角平分线交于点 ,则可计算 的角度,请写出计算过程;
