河南省三门峡市2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-06-10 类型:期中考试
一、单选题
-
1. 的算术平方根是( )A、 B、 C、 D、2. 在平面直角坐标系中,点P(3,﹣2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 2022年,中国将举办第二十四届冬季奥林匹克运动会,如图,通过平移吉样物“冰墩墩”可以得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 在实数 , , , , , , , 中,无理数的个数是( )A、5 B、4 C、3 D、25. 在平面直角坐标系中,将点(﹣4,3)向右平移2个单位,再向下平移2个单位后,得到的点的坐标为( )A、(﹣6,1) B、(﹣2,1) C、(﹣6,5) D、(﹣2,5)6. 如图, ,若 ,则 的度数为( )
4. 在实数 , , , , , , , 中,无理数的个数是( )A、5 B、4 C、3 D、25. 在平面直角坐标系中,将点(﹣4,3)向右平移2个单位,再向下平移2个单位后,得到的点的坐标为( )A、(﹣6,1) B、(﹣2,1) C、(﹣6,5) D、(﹣2,5)6. 如图, ,若 ,则 的度数为( ) A、 B、 C、 D、7. 估计 的值在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 下列命题是真命题的个数是( )
A、 B、 C、 D、7. 估计 的值在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 下列命题是真命题的个数是( )①两点确定一条直线 ②两点之间,线段最短 ③对顶角相等 ④内错角相等
A、1 B、2 C、3 D、49. 下列语句正确的是( )A、在平面直角坐标系中, 与 表示两个不同的点 B、平行于 轴的直线上所有点的横坐标都相同、 C、若点 在 轴上,则 D、点 到 轴的距离为310. 一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( ) A、纸带①的边线平行,纸带②的边线不平行 B、纸带①、②的边线都平行 C、纸带①的边线不平行,纸带②的边线平行 D、纸带①、②的边线都不平行
A、纸带①的边线平行,纸带②的边线不平行 B、纸带①、②的边线都平行 C、纸带①的边线不平行,纸带②的边线平行 D、纸带①、②的边线都不平行二、填空题
-
11. 写出一个比2大比3小的无理数(用含根号的式子表示) .
12. 如图,某单位要在河岸 上建一个水泵房引水到C处,他们的做法是:过点C作 于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 . 13. 如图,一条公路的两侧铺设了两条平行管道,如果公路一侧铺设的管道与纵向连通管道的角度为 ,那么,为了使管道能够顺利对接,另一侧铺设的纵向连通管道与公路的角度为.
13. 如图,一条公路的两侧铺设了两条平行管道,如果公路一侧铺设的管道与纵向连通管道的角度为 ,那么,为了使管道能够顺利对接,另一侧铺设的纵向连通管道与公路的角度为. 14. 中国象棋在我国有着三千多年的历史,如图是一局象棋残局,若表示棋子“馬”和“車"的点的坐标分别为 , ,则表示棋子“炮”的点的坐标为.
14. 中国象棋在我国有着三千多年的历史,如图是一局象棋残局,若表示棋子“馬”和“車"的点的坐标分别为 , ,则表示棋子“炮”的点的坐标为.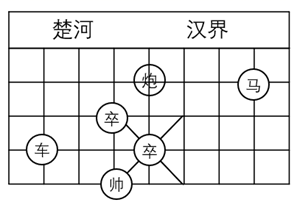 15. 大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分,于是可以用 表示 的小数部分.若 ,其中x是整数,且 ,写出x﹣y的相反数.
15. 大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分,于是可以用 表示 的小数部分.若 ,其中x是整数,且 ,写出x﹣y的相反数.三、解答题
-
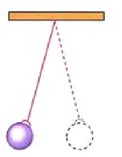
16. 计算:(1)、(2)、17. 已知:x﹣6和3x+14是a的两个不同的平方根,2y+2是a的立方根.(1)、求x,y,a的值;(2)、求1﹣4x的算术平方根.18. 如图,一根细线上端固定,下端系一个小重物,让这个小重物来回自由摆动,来回摆动一次所用的时间 (单位: )与细线的长度 (单位: )之间满足关系 ,当细线的长度为 时,小重物来回摆动一次所用的时间是多少(结果保留小数点后一位)?(参考数据: , )
 19. 如图,已知 , , .
19. 如图,已知 , , .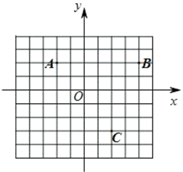 (1)、写出点 到 轴的距离;(2)、连接 、 、 ,求 的面积;(3)、点 在 轴上,当 的面积是6时,求出点 的坐标.20. 已知点 .(1)、当点 在 轴上时,点 的坐标为;(2)、点 的坐标为 ,且直线 轴,求点 的坐标.(3)、点 到 轴、 轴的距离相等,求点 的坐标.21. 如图,射线 平外 ,且 .求证: .
(1)、写出点 到 轴的距离;(2)、连接 、 、 ,求 的面积;(3)、点 在 轴上,当 的面积是6时,求出点 的坐标.20. 已知点 .(1)、当点 在 轴上时,点 的坐标为;(2)、点 的坐标为 ,且直线 轴,求点 的坐标.(3)、点 到 轴、 轴的距离相等,求点 的坐标.21. 如图,射线 平外 ,且 .求证: .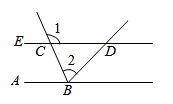 22. 2018年9月,习近平总书记在全国教育大会上提出“要树立健康第一的教育理念,开齐开足体育课,帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志”,依据《国家学生体质健康标准》“使每个学生掌握至少两项终身受益的体育锻炼项目”的目标要求,我市某学校增设了篮球项目的教学,如图①,为该校放置在水平操场上的篮球架的横截面图形,初始状志时,篮球架的横梁 平行于 ,主柱 垂直于地面, 与上拉杆 形成的角度为 ,且 ,这一篮球架可以通过调整 和后拉杆 的位置来调整篮筐的高度.在调整 的高度时,为使 和 平行,需要改变 和 的度数,如图②,调整 使其上升到 的位置,此时, 与 平行, ,并且点 , , 在同一直线上,请你帮忙求出 的大小.
22. 2018年9月,习近平总书记在全国教育大会上提出“要树立健康第一的教育理念,开齐开足体育课,帮助学生在体育锻炼中享受乐趣、增强体质、健全人格、锤炼意志”,依据《国家学生体质健康标准》“使每个学生掌握至少两项终身受益的体育锻炼项目”的目标要求,我市某学校增设了篮球项目的教学,如图①,为该校放置在水平操场上的篮球架的横截面图形,初始状志时,篮球架的横梁 平行于 ,主柱 垂直于地面, 与上拉杆 形成的角度为 ,且 ,这一篮球架可以通过调整 和后拉杆 的位置来调整篮筐的高度.在调整 的高度时,为使 和 平行,需要改变 和 的度数,如图②,调整 使其上升到 的位置,此时, 与 平行, ,并且点 , , 在同一直线上,请你帮忙求出 的大小.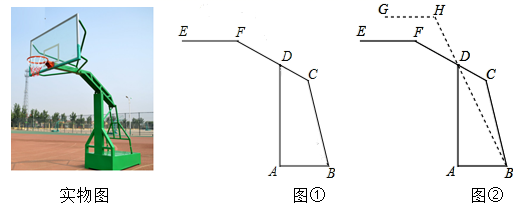 23. 综合与实践
23. 综合与实践问题背景
如图,在平面直角坐标系中,点A的坐标为(﹣3,5),点B的坐标为(0,1),点C的坐标为(4,5),将线段AB沿AC方向平移,平移距离为线段AC的长度.
 (1)、动手操作:画出AB平移后的线段CD,直接写出B的对应点D的坐标;(2)、探究证明“”连接BD,试探究∠BAC,∠BDC的数量关系,并证明你的结论;(3)、拓展延伸:若点E在线段BD上,连接AD,AE,且满足∠EAD=∠CAD,请求出∠ADB:∠AEB的值,并写出推理过程.
(1)、动手操作:画出AB平移后的线段CD,直接写出B的对应点D的坐标;(2)、探究证明“”连接BD,试探究∠BAC,∠BDC的数量关系,并证明你的结论;(3)、拓展延伸:若点E在线段BD上,连接AD,AE,且满足∠EAD=∠CAD,请求出∠ADB:∠AEB的值,并写出推理过程.