四川省攀枝花市2021届高三文数三模试卷
试卷更新日期:2021-06-10 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则集合 ( ).A、 B、 C、 D、2. 若 是虚数单位,复数 ,则 的共扼复数 在复平面上对应的点位于( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 2022年起,我市将试行“ ”的普通高考新模式,即语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目,为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图,甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )
 A、甲的物理成绩领先年级平均分最多 B、甲有2个科目的成绩低于年级平均分 C、甲的成绩最好的前两个科目是化学和地理 D、对甲而言,物理、化学、地理是比较理想的一种选科结果4. 已知向量 , 满足 , ,且 ,则 , 的夹角大小为( ).A、 B、 C、 D、5. 已知函数 ,则曲线 的所有切线中,斜率最大的切线方程为( )A、 B、 C、 D、6. 在 中,角 的对边分别为 ,且 , , ,则 ( ).A、 B、 C、 D、37. 若函数 在 上的最大值为4,则 的取值范围为( )A、 B、 C、 D、8. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为 的等腰直角三角形,俯视图是圆心角为 的扇形,则该几何体的表面积为( ).
A、甲的物理成绩领先年级平均分最多 B、甲有2个科目的成绩低于年级平均分 C、甲的成绩最好的前两个科目是化学和地理 D、对甲而言,物理、化学、地理是比较理想的一种选科结果4. 已知向量 , 满足 , ,且 ,则 , 的夹角大小为( ).A、 B、 C、 D、5. 已知函数 ,则曲线 的所有切线中,斜率最大的切线方程为( )A、 B、 C、 D、6. 在 中,角 的对边分别为 ,且 , , ,则 ( ).A、 B、 C、 D、37. 若函数 在 上的最大值为4,则 的取值范围为( )A、 B、 C、 D、8. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为 的等腰直角三角形,俯视图是圆心角为 的扇形,则该几何体的表面积为( ). A、 B、 C、 D、9. 过直线 上的点 作圆 的两条切线 , ,若直线 , 关于直线 对称,则 ( ).A、 B、 C、 D、10. 设 , 是双曲线 的左、右两个焦点,若双曲线右支上存在一点 ,使得 ( 为坐标原点),且 ,则双曲线的离心率为( ).A、 B、 C、 D、11. 已知 , , , 为球 的球面上的四个点, , ,球 的表面积为 ,则三棱锥 的体积的最大值为( ).A、 B、 C、 D、12. 已知 , , ,且 ,则( ).A、 B、 C、 D、
A、 B、 C、 D、9. 过直线 上的点 作圆 的两条切线 , ,若直线 , 关于直线 对称,则 ( ).A、 B、 C、 D、10. 设 , 是双曲线 的左、右两个焦点,若双曲线右支上存在一点 ,使得 ( 为坐标原点),且 ,则双曲线的离心率为( ).A、 B、 C、 D、11. 已知 , , , 为球 的球面上的四个点, , ,球 的表面积为 ,则三棱锥 的体积的最大值为( ).A、 B、 C、 D、12. 已知 , , ,且 ,则( ).A、 B、 C、 D、二、填空题
-
13. 已知 ,且角 为第三象限角,则 .14. 设x,y满足约束条件 ,则 的最大值为 .15. 已知 , 分别是椭圆 的下顶点和左焦点,过 且倾斜角为60°的直线 交椭圆 于 点(异于点 ),且 的周长为 ,则 的面积为 .16. 已知函数 ,给出下列结论:
① 是周期函数;
② 在区间 上是增函数;
③若 ,则 ;
④函数 在区间 上有且仅有1个零点.
其中正确结论的序号是 . (将你认为正确的结论序号都填上)
三、解答题
-
17. 已知 是数列 的前 项的和, ,且 , , 成等差数列.(1)、求 的通项公式;(2)、设 ,记 是数列 的前 项的和.求当 取最大值时的 的值.18. 第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,也是继2G、3G和4G系统之后的延伸.5G的性能目标是高数据速率、减少延迟、节省能源、降低成本、提高系统容量和大规模设备连接.某大学为了解学生对5G相关知识的了解程度,随机抽取男女学生各50人进行问卷测评,所得分数的频率分布直方图如图所示,并规定得分在80分以上为“比较了解”.

附: ,其中 .
0.05
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
(1)、求 的值,并估计该大学学生对5G比较了解的概率;(2)、已知对5G比较了解的样本中男女比例为4:1.完成下列 列联表,并判断有多大把握认为对5G比较了解与性别有关;比较了解
不太了解
合计
男性
女性
合计
(3)、用分层抽样的方式从得分在50分以下的样本中抽取6人,再从6人中随机选取2人,求至少有1人得分低于40分的概率.19. 如图,三棱锥 中, 面 ,△ 为正三角形,点 在棱 上,且 , 、 分别是棱 、 的中点,直线 与直线 交于点 ,直线 与直线 交于点 , , .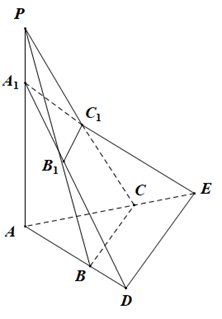 (1)、求证: ;(2)、求几何体 的体积.20. 已知函数 .(1)、当 时,求函数 的单调区间;(2)、若函数 有两个极值点,且极小值大于 ,求实数 的取值范围.21. 已知抛物线 的准线与直线 的距离为4.(1)、求抛物线 的方程;(2)、 、 为抛物线 上的两个不重合的动点,且线段 的中点 在直线 上,设线段 的垂直平分线为直线 .
(1)、求证: ;(2)、求几何体 的体积.20. 已知函数 .(1)、当 时,求函数 的单调区间;(2)、若函数 有两个极值点,且极小值大于 ,求实数 的取值范围.21. 已知抛物线 的准线与直线 的距离为4.(1)、求抛物线 的方程;(2)、 、 为抛物线 上的两个不重合的动点,且线段 的中点 在直线 上,设线段 的垂直平分线为直线 .①证明: 经过定点 ;
②若 交 轴于点 ,设 的面积为 ,求 的最大值.