四川省德阳市2021届高三理数三模数学试卷
试卷更新日期:2021-06-10 类型:高考模拟
一、单选题
-
1. 设 是虚数单位.若复数 是纯虚数,则 的值为( )A、-3 B、1 C、-1 D、32. 已知集合 , .则 ( )A、 B、 C、 D、3. 如图为某商场一天营业额的扇形统计图,根据统计图你不能得出的信息为( )
 A、该商场家用电器销售额为全商场营业额的40% B、服装鞋帽和百货日杂共售出29000元 C、副食的销售额为该商场营业额的10% D、家用电器部所得利润最高4. 已知 , :向量 与 共线,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 阅读如图所示的框图,运行相应的程序,输出 的值等于( )
A、该商场家用电器销售额为全商场营业额的40% B、服装鞋帽和百货日杂共售出29000元 C、副食的销售额为该商场营业额的10% D、家用电器部所得利润最高4. 已知 , :向量 与 共线,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 阅读如图所示的框图,运行相应的程序,输出 的值等于( ) A、-3 B、-10 C、0 D、-26. 如图,在正四棱柱 中,点 是平面 内一点,则三棱锥 的主(正)视图与左(侧)视图的面积之比为( )
A、-3 B、-10 C、0 D、-26. 如图,在正四棱柱 中,点 是平面 内一点,则三棱锥 的主(正)视图与左(侧)视图的面积之比为( ) A、3:2 B、2:1 C、2:3 D、1:17. 设函数 在R上可导,其导函数为 ,且函数 在 处取得极小值,则函数 的图像可能是( )A、
A、3:2 B、2:1 C、2:3 D、1:17. 设函数 在R上可导,其导函数为 ,且函数 在 处取得极小值,则函数 的图像可能是( )A、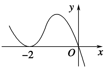 B、
B、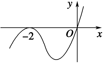 C、
C、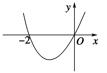 D、
D、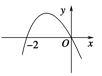 8. 已知抛物线 的弦 的中点的横坐标为3,则 的最大值为( )A、2 B、4 C、6 D、89. 设函数 的图象关于直线 对称,它的周期是π,则下列说法正确的个数为( )
8. 已知抛物线 的弦 的中点的横坐标为3,则 的最大值为( )A、2 B、4 C、6 D、89. 设函数 的图象关于直线 对称,它的周期是π,则下列说法正确的个数为( )①将 的图象向右平移 个单位长度得到函数 的图象;② 的图象过点(0,1);③ 的图象的一个对称中心是 ;④ 在 上是减函数
A、1 B、2 C、3 D、410. 若数列 对于任意的正整数 满足: ,且 ,则称数列 为“积增数列”.已知“积增数列” 中, ,数列 的前 项和为 ,则对于任意的正整数 ,有( )A、 B、 C、 D、11. 过双曲线 的左顶点 作斜率为1的直线 ,若直线 与双曲线 的两条渐近线分别相交于点 、 ,且 ,则双曲线的离心率为( )( 为原点)A、 B、 C、 D、12. 已知函数 ,若存在 ,使 ,则实数 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 等比数列 满足 , ,则 .14. 已知实数 满足 ,则目标函数 的最大值为 .15. 的展开式中的常数项为 .16. 在直角三角形 中, , 是斜边 的中点,将 沿直线 翻折,若在翻折过程中存在某个位置,使得 ,则 边长的最大值为.
三、解答题
-
17. 为了更好的开展高中数学综合实践课的教学,结合高中数学与物理紧密联系的特点,某高级中学数学组与物理组进行联合教学实践活动.在一次实践活动中,某班学生分成五组进行物理实验(研究某物理现象中两个物理量 、 之间的关系),得到五组数据如下表所示.
组号
1
2
3
4
5
物理量
12
11
13
10
9
物理量
27
25
29
24
20
参考公式: , .
(1)、为了减少一定的运算量,同学们决定用前三组的数据研究两个物理量 、 的线性回归方程,并由该回归方程预估第4,5组物理量 的值,若产生的残差的绝对值不超过1,则认为本次实践活动成功.请问本次实践活动是否成功?并说明理由;(2)、老师打算从这五组学生中随机选取两组学生进行校本科研课题:《数学与物理深度融合研究》的问卷调查,记组号差的绝对值为 ,求 的分布列与数学期望.18. 在 中, , , , 为 内一点,且 .(1)、若 ,求 ;(2)、若 ,设 ,求 .19. 四棱锥 中, , , ,平面 平面 ,点 为 的中点. (1)、求证:向量 、 、 共面;(2)、若 ,求二面角 的余弦值.20. 设圆 的圆心为 ,过点 且与 轴不重合的直线交明 于 、 两点,过 作 的平行线交 于点 .(1)、证明 为定值,并写出点 的轨迹 的方程;(2)、已知点 , ,过点 的直线 与曲线 交于 、 两点.记 与 的面积分别为 和 ,求 的最大值.
(1)、求证:向量 、 、 共面;(2)、若 ,求二面角 的余弦值.20. 设圆 的圆心为 ,过点 且与 轴不重合的直线交明 于 、 两点,过 作 的平行线交 于点 .(1)、证明 为定值,并写出点 的轨迹 的方程;(2)、已知点 , ,过点 的直线 与曲线 交于 、 两点.记 与 的面积分别为 和 ,求 的最大值.