山东省聊城市2021届高三数学三模试卷
试卷更新日期:2021-06-10 类型:高考模拟
一、单选题
-
1. 已知集合 , ,若 ,则实数 的值为( )A、0 B、1 C、2 D、32. 已知 , 为虚数单位,若 为实数,则 的值为( )A、 B、 C、 D、3. 函数 的图象大致为( )A、
 B、
B、 C、
C、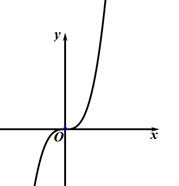 D、
D、 4. 已知直线 ,圆 .则“ ”是“ 与 相切”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件5. 声强级 (单位:dB)由公式 给出,其中 为声强(单位:W/m2)一般正常人听觉能忍受的最高声强级为120dB,平时常人交谈时声强级约为60dB,那么一般正常人能忍受的最高声强是平时常人交谈时声强的( )A、104倍 B、105倍 C、106倍 D、107倍6. 在某次脱贫攻坚表彰会上,共有36人受到表彰,其中男性多于女性,现从中随机选出2人作为代表上台领奖,若选出的两人性别相同的概率为 ,则受表彰人员中男性人数为( )A、15 B、18 C、21 D、15或217. 在 中, , , ,M为BC中点,O为 的内心,且 ,则 ( )A、 B、 C、 D、18. 已知A , B , C是双曲线 上的三点,直线AB经过原点O , AC经过右焦点F , 若 ,且 ,则该双曲线的离心率为( )A、 B、 C、 D、
4. 已知直线 ,圆 .则“ ”是“ 与 相切”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件5. 声强级 (单位:dB)由公式 给出,其中 为声强(单位:W/m2)一般正常人听觉能忍受的最高声强级为120dB,平时常人交谈时声强级约为60dB,那么一般正常人能忍受的最高声强是平时常人交谈时声强的( )A、104倍 B、105倍 C、106倍 D、107倍6. 在某次脱贫攻坚表彰会上,共有36人受到表彰,其中男性多于女性,现从中随机选出2人作为代表上台领奖,若选出的两人性别相同的概率为 ,则受表彰人员中男性人数为( )A、15 B、18 C、21 D、15或217. 在 中, , , ,M为BC中点,O为 的内心,且 ,则 ( )A、 B、 C、 D、18. 已知A , B , C是双曲线 上的三点,直线AB经过原点O , AC经过右焦点F , 若 ,且 ,则该双曲线的离心率为( )A、 B、 C、 D、二、多选题
-
9. 对具有相关关系的两个变量x和y进行回归分折时,经过随机抽样获得成对的样本点数据 ,则下列结论正确的是( )A、若两变量x , y具有线性相关关系,则回归直线至少经过一个样本点 B、若两变量x , y具有线性相关关系,则回归直线一定经过样本点中心 C、若以模型 拟合该组数据,为了求出回归方程,设 ,将其变换后得到线性方程 ,则a , b的估计值分别是3和6. D、用 来刻画回归模型的拟合效果时,若所有样本点都落在一条斜率为非零实数的直线上,则 的值为110. 将函数 的图象向右平移 个单位长度,再将所有点的横坐标缩短到原来的 ,纵坐标不变,得到函数 的图象,则下面对函数 的叙述中正确的是( )A、函效 的最小正周期为 B、函数 图象关于点 对称 C、函数 在区间 内单调递增 D、函数 图象关于直线 对称11. 已知实数a、b , 下列说法一定正确的是( )A、若 ,则 B、若 ,则 C、若 , , ,则 的最小值为8 D、若 ,则12. 已知等边三角形ABC的边长为6,M , N分别为AB , AC的中点,将 沿MN折起至 ,在四棱锥 中,下列说法正确的是( )A、直线MN∥平面 B、当四棱锥 体积最大时,二面角 为直二面角 C、在折起过程中存在某位置使BN⊥平面 D、当四棱 体积最大时,它的各顶点都在球O的球面上,则球O的表面积为
三、填空题
-
13. 数列1,1,2,3,5,8,13,21,34,…称为斐波那契数列,是意大利著名数学家斐波那契于1202年在他写的《算盘全书》提出的,该数列的特点是:从第三起,每一项都等于它前面两项的和.在该数列的前2021项中,奇数的个数为 .14. 曲线 在 处的切线的倾斜角为 ,则 .15. 已知点 ,过抛物线 .上一点P作 的垂线,垂足为B , 若 ,则 .16. 已知函数 有三个不同的零点 , , ,其中 ,则 的值为 .
四、解答题
-
17. 在 中,角A , B , C的对边分别为a , b , c , 且 ,(1)、求角B的大小;(2)、已知点D满足 ,且 ,若 , ,求AC.18. 在① , , 成等比数列② ,③ ,这三个条件中任选一个,补充在下面的问题中,并做出解答.
已知 是公差不为零的等差数列, 为其n前项和, ,_______, 是等比数列, , ,公比 .
(1)、求数列 , 的通项公式;(2)、数列 和 的所有项分别构成集合A , B , 将 的元素按从小到大依次排列构成一个新数列 ,求 .19. 如图,在平面四边形ABCD中, , , ,以BD为折痕把 折起,使点A到达点P的位置,且 . (1)、证明: ;(2)、若M为PB的中点,二面角 的大小为60°,求直线PC与平面MCD所成角的正弦值.20. 2021年3月5日李克强总即在政府作报告中特别指出:扎实做好碳达峰,碳中和各项工作,制定2030年前碳排放达峰行动方案,优化产业结构和能源结构.某环保机器制造商为响应号召,对一次购买2台机器的客户推出了两种超过机器保修期后5年内的延保维修方案:
(1)、证明: ;(2)、若M为PB的中点,二面角 的大小为60°,求直线PC与平面MCD所成角的正弦值.20. 2021年3月5日李克强总即在政府作报告中特别指出:扎实做好碳达峰,碳中和各项工作,制定2030年前碳排放达峰行动方案,优化产业结构和能源结构.某环保机器制造商为响应号召,对一次购买2台机器的客户推出了两种超过机器保修期后5年内的延保维修方案:方案一;交纳延保金5000元,在延保的5年内可免费维修2次,超过2次每次收取维修费1000元;
方案二:交纳延保金6230元,在延保的5和内可免费维修4次,超过4次每次收取维修费t元;
制造商为制定的收取标准,为此搜集并整理了200台这种机器超过保修期后5年内维修的次数,统计得到下表
维修次数
0
1
2
3
机器台数
20
40
80
60
以这200台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示2台机器超过保修期后5年内共需维修的次数.
(1)、求X的分布列;(2)、以所需延保金与维修费用之和的均值为决策依据,为使选择方案二对客户更合算,应把t定在什么范围?