江苏省南通市2021届高三下学期数学5月四模试卷

试卷更新日期：2021-06-09 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {1 ， 2 ， 3}$ ， $B = {- 1 ， 0 ， 1 ， 2}$ ，若 $M \subseteq A$ 且 $M \subseteq B$ ，则 $M$ 的个数为（）

A、1 B、3 C、4 D、6

查看试题解析
2. 已知向量 $\vec{a} = (\sin θ, 1)$ ， $\vec{b} = (2 \sin θ, - 1)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则 $\cos 2 θ =$ （）

A、0 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、-1

查看试题解析
3. 已知等比数列 ${a_{n}}$ 的公比为 $q$ ，则“ $q < 1$ ”是“ $| a_{4} | > | a_{5} |$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 4位优秀党务工作者到3个基层单位进行百年党史宣讲，每人宣讲1场，每个基层单位至少安排1人宣讲，则不同的安排方法数为（）

A、81 B、72 C、36 D、6

查看试题解析
5. 我国于2021年5月成功研制出目前国际上超导量子比特数量最多的量子计算原型机“祖冲之号”，操控的超导量子比特为62个.已知1个超导量子比特共有“ $| 0 >$ ， $| 1 >$ ”2种叠加态，2个超导量子比特共有“ $| 00 >$ ， $| 01 >$ ， $| 10 >$ ， $| 11 >$ ”4种叠加态，3个超导量子比特共有“ $| 000 >$ ， $| 001 >$ ， $| 010 >$ ， $| 011 >$ ， $| 100 >$ ， $| 101 >$ ， $| 110 >$ ， $| 111 >$ ”8种叠加态，…，只要增加1个超导量子比特，其叠加态的种数就呈指数级增长.设62个超导量子比特共有 $N$ 种叠加态，则 $N$ 是一个（）位的数.(参考数据： $\lg 2 \approx 0.3010$ )

A、18 B、19 C、62 D、63

查看试题解析
6. 在 $(1 + 2 x^{2}) {(x + \frac{1}{x})}^{10}$ 的展开式中，常数项为（）

A、210 B、252 C、462 D、672

查看试题解析
7. 双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ ( $a > 0$ ， $b > 0$ )的左､右焦点分别为 $F_{1}$ ， $F_{2}$ ，若 $C$ 上存在点 $P$ 满足 $∠ F_{2} P O = 2 ∠ F_{1} P O = \frac{π}{3}$ ，则该双曲线的离心率为（）

A、 $\sqrt{3} + 1$ B、 $\sqrt{2} + 1$ C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
8. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $N$ 为 $B C$ 的中点.当点 $M$ 在平面 $D C C_{1} D_{1}$ 内运动时，有 $M N / /$ 平面 $A_{1} B D$ ，则线段 $M N$ 的最小值为（）

A、1 B、 $\frac{\sqrt{6}}{2}$ C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析

二、多选题

9. 新中国成立以来，我国共进行了7次人口普查，这7次人口普查的城乡人口数据如下：

根据该图数据，这7次人口普查中（）

A、城镇人口数均少于乡村人口数 B、乡村人口数达到最高峰是第4次 C、和前一次相比，城镇人口比重增量最大的是第7次 D、城镇人口总数逐次增加

查看试题解析
10. 下列结论正确的是（）

A、若复数 $z$ 满足 $z + \bar{z} = 0$ ，则 $z$ 为纯虚数 B、若复数 $z$ 满足 $\frac{1}{z} \in R$ ，则 $z \in R$ C、若复数 $z$ 满足 $z^{2} \geq 0$ ，则 $z \in R$ D、若复数 $z_{1}$ ， $z_{2}$ 满足 $z_{1}^{2} + z_{2}^{2} = 0$ ，则 $z_{1} = z_{2} = 0$

查看试题解析
11. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，且 $C = \frac{π}{2}$ ，将 $△ A B C$ 分别绕边 $a$ ， $b$ ， $c$ 所在的直线旋转一周，形成的几何体的体积分别记为 $V_{a}$ ， $V_{b}$ ， $V_{c}$ ，侧面积分别记为 $S_{a}$ ， $S_{b}$ ， $S_{c}$ ，则（）

A、 $V_{a} + V_{b} \geq 2 V_{c}$ B、 $S_{a} + S_{b} \geq 2 S_{c}$ C、 $\frac{1}{V_{a}^{2}} + \frac{1}{V_{b}^{2}} = \frac{1}{V_{c}^{2}}$ D、 $\frac{1}{S_{a}^{2}} + \frac{1}{S_{b}^{2}} = \frac{1}{S_{c}^{2}}$

查看试题解析
12. 已知定义在 $R$ 上的函数 $f (x) = | \sqrt{1 + \sin 2 x} - \sqrt{1 - \sin 2 x} |$ ，则（）

A、 $f (- x) = f (x)$ B、 $f (x + \frac{π}{2}) = f (x)$ C、 $f (x)$ 的最大值为2 D、不等式 $f (x) \geq 2 \cos x$ 的解集为 ${x ∣ \frac{π}{4} + 2 k π \leq x < \frac{7 π}{4} + 2 k π ， k \in z}$

查看试题解析

三、填空题

13. 已知角 $α$ 的终边经过点 $(- 3, 4)$ ，则 $\cos (\frac{3 π}{2} + α)$ 的值是.

查看试题解析
14. 设曲线 $y = f (x)$ 在 $x = 0$ 处的切线斜率为1，试写出满足题设的一个 $f (x) =$ .

查看试题解析
15. 舒腾尺是荷兰数学家舒腾(1615-1660)设计的一种作图工具，如图， $O$ 是滑槽 $A B$ 的中点，短杆 $O N$ 可绕 $O$ 转动，长杆 $M N$ 通过 $N$ 处的铰链与 $O N$ 连接， $M N$ 上的栓子 $D$ 可沿滑槽 $A B$ 滑动.当点 $D$ 在滑槽 $A B$ 内作往复移动时，带动点 $N$ 绕 $O$ 转动，点 $M$ 也随之而运动.记点 $N$ 的运动轨迹为 $C_{1}$ ，点 $M$ 的运动轨迹为 $C_{2}$ .若 $O N = D N = 1$ ， $M N = 3$ ，过 $C_{2}$ 上的点 $P$ 向 $C_{1}$ 作切线，则切线长的最大值为.

查看试题解析

16. 甲､乙､丙三支足球队进行双循环赛(任意两支球队都要在自己的主场和对方的主场各赛一场).根据比赛规则，胜一场得3分，平一场得1分，负一场得0分.比赛进行中的统计数据如下表：

	已赛场数	胜的场数	平的场数	负的场数	积分
甲	4	2	1	1	7
乙	3	0	2	1	2
丙	3	1	1	1	4

根据表格中的信息可知：

(1)、还需进行场比赛，整个双循环赛全部结束；

(2)、在与乙队的比赛中，甲队共得了分.

查看试题解析

四、解答题

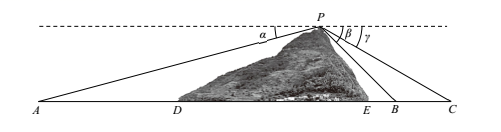
17. 已知等比数列 ${a_{n}}$ 的各项均为正数，且 $a_{6} = 2$ ， $a_{4} + a_{5} = 12$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = a_{1} a_{3} a_{5} \dots a_{2 n - 1}$ ， $n \in N *$ ，求数列 ${b_{n}}$ 的最大项.

查看试题解析
18. 如图， $A$ ， $B$ ， $C$ 为山脚两侧共线的三点，在山顶 $P$ 处观测三点的俯角分别为 $α$ ， $β$ ， $γ$ .现测得 $α = 15^{\circ}$ ， $β = 45^{\circ}$ ， $γ = 30^{\circ}$ ， $A D = \frac{5}{2} km$ ， $E B = \frac{1}{2} km$ ， $B C = 1 km$ .计划沿直线 $A C$ 开通一条穿山隧道，试求出隧道 $D E$ 的长度.

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中，平面 $P A D ⊥$ 平面 $A B C D$ ， $P A = P D$ ， $A B / / C D$ ， $A B ⊥ A D$ ， $A B = 1$ ， $A D = 2$ ， $C D = 3$ .直线 $P B$ 与平面 $A B C D$ 所成的角为 $45 °$ .

(1)、求证： $P B ⊥ B C$ ；

(2)、求二面角 $A - P B - C$ 的正弦值.

查看试题解析
20. 已知 $P$ 为抛物线 $C ： y^{2} = 4 x$ 上位于第一象限的点， $F$ 为 $C$ 的焦点， $P F$ 与 $C$ 交于点 $Q$ (异于点 $P$ ).直线 $l$ 与 $C$ 相切于点 $P$ ，与 $x$ 轴交于点 $M$ .过点 $P$ 作 $l$ 的垂线交 $C$ 于另一点 $N$ .

(1)、证明：线段 $M P$ 的中点在定直线上；

(2)、若点 $P$ 的坐标为 $(2 ， 2 \sqrt{2})$ ，试判断 $M$ ， $Q$ ， $N$ 三点是否共线.

查看试题解析
21. 在医学上，为了加快对流行性病毒的检测速度，常采用“混检”的方法：随机的将若干人的核酸样本混在一起进行检测，若检测结果呈阴性，则认定该组每份样本均为阴性，无需再检测；若检测结果呈阳性，则还需对该组的每份样本逐个重新检测，以确定每份样本是否为阳性.设某流行性病毒的感染率为 $p$ .

(1)、若 $p = 0.005$ ，混检时每组10人，求每组检测次数的期望值；

(2)、混检分组的方法有两种：每组10人或30人.试问这两种分组方法的优越性与 $p$ 的值是否有关？
(参考数据： ${0.995}^{10} \approx 0.9511$ ， ${0.995}^{30} \approx 0.8604$ )

查看试题解析
22. 已知函数 $f (x) = (x^{2} + m x + 1) e^{x}$ ， $m \in R$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、若不等式 $x^{2} - m x + 1 + e^{x + 2} \geq 0$ 恒成立，求实数 $m$ 的取值范围.

查看试题解析