江苏省南京市2020-2021学年七年级下学期期末模拟试卷

试卷更新日期：2021-06-08 类型：期末考试

进入出卷网下载

一、选择题

1. 下列语句中，是真命题的是（）

A、相等的角是对顶角 B、同旁内角互补 C、过一点不只有一条直线与已知直线垂直 D、对于直线 a、b、c，如果 b∥a，c∥a，那么 b∥c

查看试题解析
2. 甲型H1N1流感病毒的直径大约是0.000000081米，用科学记数法可表示为（）

A、8.1×10^﹣⁹米 B、8.1×10^﹣⁸米 C、81×10^﹣⁹米 D、0.81×10^﹣⁷米

查看试题解析
3. 已知x,y满足方程 ${\begin{matrix} 2 x + y = 4 \\ x + 2 y = 5 \end{matrix}$ ，则x-y等于（）

A、9 B、3 C、1 D、-1

查看试题解析
4. 已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°)，其中A，B两点分别落在直线m，n上，若∠1=40°，则∠2的度数为（）

A、10° B、20° C、30° D、40°

查看试题解析
5. 下列式子中，计算正确的是（）

A、 ${(- a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $(a + 2) (a - 2) = a^{2} - 2$ C、 $(a + 5) (a - 2) = a^{2} + 3 a - 10$ D、 $3 a^{3} \cdot 2 a^{2} = 6 a^{6}$

查看试题解析
6. 已知（m﹣4）x^|m^﹣3|＋2＞6是关于x的一元一次不等式，则m的值为（）

A、4 B、2 C、4或2 D、不确定

查看试题解析

二、填空题

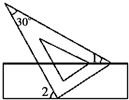
7. 已知有理数 $a$ ， $b$ 满足 $a^{2} - b^{2} = 3^{- 1}$ ，则 ${(a + b)}^{3} {(a - b)}^{3}$ 的值是.

查看试题解析
8. 若n边形内角和为900°，则边数n= ．

查看试题解析
9. 已知5^x＝3，5^y＝2，则5^x+3y＝.

查看试题解析
10. 若关于x，y的二元一次方程组 ${\begin{cases} x - y = 4 k \\ x + y = 2 k \end{cases}$ 的解也是二元一次方程组x-3y=6的解，则k等于．

查看试题解析
11. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于x、y的方程ax-by=-15的一个解，且a+b=-3，则5a-2b= .

查看试题解析
12. 若多项式x²+kx﹣6有一个因式是（x﹣2），则k= ．

查看试题解析
13. 如图，将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上，如果∠1=27°，那么∠2=°

查看试题解析
14. 已知 $a < 2$ ，如果一个正方形的面积是 $(a^{2} - 4 a + 4) c m^{2}$ ，则这个正方形的周长是cm．

查看试题解析
15. 如图，六边形ABCDEF内部有一点G，连结BG、DG. 若 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 + ∠ 5 = 440 °$ ，则∠BGD的大小为度.

查看试题解析
16. 如图，线段AB，AC是两条绕点A可以自由旋转的线段（但点A，B，C始终不在同一条直线上），已知AB=5，AC=7，点D，E分别是AB，BC的中点，则四边形BEFD面积的最大值是.

查看试题解析

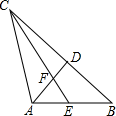
三、解答题

17. 化简：

(1)、(-2x²)³+4x³·x³-x·x⁵

(2)、(x+2)²-x(x-1)+1

查看试题解析
18. 因式分解

(1)、3a(x-y)-2(y-x)

(2)、(m+2)(m-2)-12

查看试题解析
19. 解下列方程组：

(1)、 ${\begin{array}{l} m - n = 2 \\ 2 m + 3 n = 14 \end{array}$ ;

(2)、 ${\begin{array}{l} 3 (y + 1) = 4 (x + 2) \\ 2 x - 3 = 1 + y \end{array}$ ．

查看试题解析
20. 阅读理解：
我们把 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} |$ 称作二阶行列式，规定它的运算法则为 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} |$ ＝ad﹣bc，如 $| \begin{array}{l} 2 \\ 4 \end{array} \begin{array}{l} 3 \\ 5 \end{array} |$ ＝2×5﹣3×4＝﹣2.如果有 $| \begin{array}{l} 2 \\ 1 \end{array} \begin{array}{l} 3 - x \\ x \end{array} |$ ＞0，求x的解集，并将解集在数轴上表示出来.

查看试题解析
21. 如图，D、E、F分别在△ABC的三条边上，DE∥AB，∠1+∠2=180°.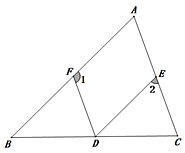

(1)、试说明：DF∥AC；

(2)、若∠1=110°，DF平分∠BDE，求∠C的度数.

查看试题解析
22. 如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上

①画出△ABC向右平移4格，再向上平移1格后的△A₁B₁C₁；

②图中BC与B₁C₁的关系是；

③图中△ABC的面积是；

④请在AB上找一点D，使得线段CD平分△ABC的面积，在图上作出线段CD。

查看试题解析
23. 如果A ， B都是由几个不同整数构成的集合，由属于A又属于B的所有整数构成的集合叫做A ， B的交集，记作A∩B ．例如：若A＝{1，2，3}，B＝{3，4，5}，则A∩B＝{3}；若A＝{0，﹣62，37，2}，B＝{2，﹣1，37，﹣5，0，19}，则A∩B＝{37，0，2}．

(1)、已知C＝{4，3}，D＝{4，5，6}，则C∩D＝{}；

(2)、已知E＝{1，m ， 2}，F＝{6，7}，且E∩F＝{m}，则m＝；

(3)、已知P＝{2m+1，2m﹣1}，Q＝{n ， n+2，n+4}，且P∩Q＝{m ， n}，如果关于x的不等式组 ${\begin{array}{l} x \geq 2 n \\ x < a \end{array}$ ，恰好有2019个整数解，求a的取值范围．

查看试题解析
24. 某中学为打造书香校园，计划购进甲、乙两种规格的书柜放置新购进的图书，调查发现，若购买甲种书柜2个、乙种书柜3个，共需资金1020元；若购买甲种书柜3个，乙种书柜4个，共需资金1440元

(1)、甲、乙两种书柜每个的价格分别是多少元?

(2)、若该校计划购进这两种规格的书柜共20个，学校至多能够提供资金3800元，请设计几种购买方案供这个学校选择.（两种规格的书柜都必须购买）

查看试题解析
25. 将一副直角三角板按如图1摆放在直线AD上 $($ 直角三角板OBC和直角三角板MON， $∠ OBC = 90^{\circ}$ ， $∠ BOC = 45^{\circ}$ ， $∠ MON = 90^{\circ}$ ， $∠ MNO = 30^{\circ})$ ，保持三角板OBC不动，将三角板MON绕点O以每秒 $8^{\circ}$ 的速度顺时针方向旋转t秒 $(0 < t < \frac{45}{4}) .$

(1)、如图2， $∠ NOD =$ 度 $($ 用含t的式子表示 $)$ ；

(2)、在旋转的过程中，是否存在t的值，使 $∠ NOD = 4 ∠ COM$ ？若存在，请求出t的值；若不存在，请说明理由.

(3)、直线AD的位置不变，若在三角板MON开始顺时针旋转的同时，另一个三角板OBC也绕点O以每秒 $2^{\circ}$ 的速度顺时针旋转.
①当 $t =$ 秒时， $∠ COM = 15^{\circ}$ ；

②请直接写出在旋转过程中， $∠ NOD$ 与 $∠ BOM$ 的数量关系 $($ 关系式中不能含 $t)$ .

查看试题解析
26. 已知： $△ A B C$ 中， $A E$ 是 $△ A B C$ 的角平分线， $A D$ 是 $△ A B C$ 的 $B C$ 边上的高，过点 $B$ 做 $B F / / A E$ ，交直线 $A D$ 于点 $F$ ．

(1)、如图1，若 $∠ A B C = 70 ° ， ∠ C = 30 °$ ，则 $∠ A F B =$ ；

(2)、若 $(1)$ 中的 $∠ A B C = a ， ∠ A C B = β$ ，则 $∠ A F B =$ ；(用 $a ， β$ 表示)

(3)、如图2， $(2)$ 中的结论还成立吗?若成立，说明理由；若不成立，请求出 $∠ A F B$ ．(用 $a ， β$ 表示)

查看试题解析