浙江省丽水市2021年初中毕业生学业考试数学模拟试卷(五)
试卷更新日期:2021-06-08 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 数1,0, ,-2中最大的是( )A、1 B、0 C、 D、-22. 下列运算正确的是( )A、a8÷a4=a2 B、(a2)2=a4 C、a2·a3=a6 D、a2+a2=2a43. 如图是由四个相同的小正方体组成的立体图形,它的主视图为( ).
 A、
A、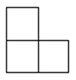 B、
B、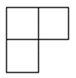 C、
C、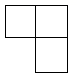 D、
D、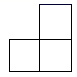 4. 无理数 在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球。从布袋里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、6. 如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
4. 无理数 在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球。从布袋里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、6. 如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )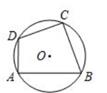 A、70° B、110° C、130° D、140°7. 如图是由七巧板拼成的正方形,则小正方形和大正方形的面积之比是( )
A、70° B、110° C、130° D、140°7. 如图是由七巧板拼成的正方形,则小正方形和大正方形的面积之比是( ) A、1:4 B、1:6 C、1:8 D、1:98. 若关于x的一元二次方程(k-1)x2+2x-2=0有实数根,则k的取值可能是( )A、-2 B、0 C、 D、19. 在边长为1的正方形组成的网格中,线段AB,CD的端点都在格点上,AB,CD交于点E,则tan∠AED的值为( )
A、1:4 B、1:6 C、1:8 D、1:98. 若关于x的一元二次方程(k-1)x2+2x-2=0有实数根,则k的取值可能是( )A、-2 B、0 C、 D、19. 在边长为1的正方形组成的网格中,线段AB,CD的端点都在格点上,AB,CD交于点E,则tan∠AED的值为( ) A、1 B、 C、2 D、10. 设m是非零实数,给出下列四个命题:①若-1<m<0,则 <m<m2;②若m>1,则 <m2<m;③若m< <m2 , 则m<0;④若m2<m< ,则0<m<1。其中是真命题的序号是( )A、①③ B、①④ C、②③ D、③④
A、1 B、 C、2 D、10. 设m是非零实数,给出下列四个命题:①若-1<m<0,则 <m<m2;②若m>1,则 <m2<m;③若m< <m2 , 则m<0;④若m2<m< ,则0<m<1。其中是真命题的序号是( )A、①③ B、①④ C、②③ D、③④二、填空题(本题有6小题,每小题4分,共24分)
-
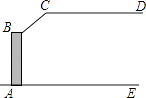
11. 分解因式:m2-25=。12. 数据-2,0,-1,2,5的中位数是。13. 一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=度.
 14. 在平面直角坐标系xOy中,直线y=x与双曲线y= 交于A,B两点。若点A,B的纵坐标分别为y1 , y2 , 则y1+y2的值为。15. 如图,将三角形纸片(△ABC)进行折叠,使点B落在边AC上,记为点D,折痕为EF。已知AB=AC=3,BC=4,若以点A,E,D为顶点的三角形与△ABC相似,则BE=。
14. 在平面直角坐标系xOy中,直线y=x与双曲线y= 交于A,B两点。若点A,B的纵坐标分别为y1 , y2 , 则y1+y2的值为。15. 如图,将三角形纸片(△ABC)进行折叠,使点B落在边AC上,记为点D,折痕为EF。已知AB=AC=3,BC=4,若以点A,E,D为顶点的三角形与△ABC相似,则BE=。 16. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥I,BF⊥I,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2测得EF=15米,FM=2米,MN=8米,∠ANE=45°。
16. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥I,BF⊥I,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2测得EF=15米,FM=2米,MN=8米,∠ANE=45°。 (1)、AB为米;(2)、矩形ABCD的面积为米2。
(1)、AB为米;(2)、矩形ABCD的面积为米2。三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17. 计算:
( )-1+ +|-2|-6sin45°
18. 解不等式组 .19. 为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).请根据图中信息解答下列问题:
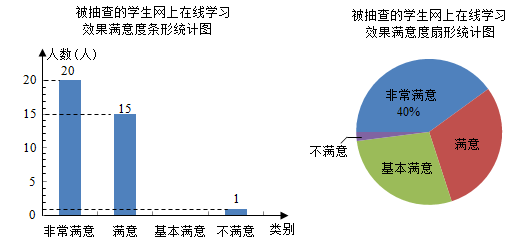 (1)、求被抽查的学生人数,并补全条形统计图;(2)、求扇形统计图中表示“满意”的扇形的圆心角度数;(3)、若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?20. 在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,点E为AC延长线上一点,连结DE,过点D作DF⊥DE,交CB的延长线于点F。
(1)、求被抽查的学生人数,并补全条形统计图;(2)、求扇形统计图中表示“满意”的扇形的圆心角度数;(3)、若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?20. 在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,点E为AC延长线上一点,连结DE,过点D作DF⊥DE,交CB的延长线于点F。 (1)、依题意补全图形。(2)、求证:CE=BF。21. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离)(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:
(1)、依题意补全图形。(2)、求证:CE=BF。21. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离)(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题: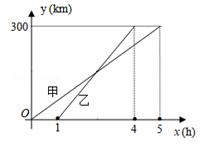 (1)、A,B两城相距千米;(2)、分别求甲、乙两车离开A城的距离y与x的关系式。(3)、求乙车出发后几小时追上甲车?22. 如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连结BD。
(1)、A,B两城相距千米;(2)、分别求甲、乙两车离开A城的距离y与x的关系式。(3)、求乙车出发后几小时追上甲车?22. 如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连结BD。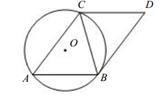 (1)、四边形ABCD是平行四边形吗?请说明理由。(2)、求证:BD是⊙O的切线。(3)、若AB=10,cos∠BAC= ,求BD的长及⊙O的半径。23. 在平面直角坐标系xOy中,抛物线y=x2-2ax+a2的顶点为A,直线y=x+3与抛物线交于点B,C(点B在点C的左侧)。
(1)、四边形ABCD是平行四边形吗?请说明理由。(2)、求证:BD是⊙O的切线。(3)、若AB=10,cos∠BAC= ,求BD的长及⊙O的半径。23. 在平面直角坐标系xOy中,抛物线y=x2-2ax+a2的顶点为A,直线y=x+3与抛物线交于点B,C(点B在点C的左侧)。 (1)、求点A的坐标。(2)、横、纵坐标都是整数的点叫做整点,记线段BC及抛物线在BC两点之间的部分围成的封闭区域(不含边界)记为W。
(1)、求点A的坐标。(2)、横、纵坐标都是整数的点叫做整点,记线段BC及抛物线在BC两点之间的部分围成的封闭区域(不含边界)记为W。①当a=0时,求出区域W内的整点个数。
②如果区域W内有2个整点,请求出a的取值范围。
24. 平面内,如图,在 ABCD中,AB=10,AD=15,tanA= ,点P为AD边上任意点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ。 (1)、当AP为何值时?点Q与点B间的距离最小。(2)、若QB⊥CD,求AP的长。(3)、若点Q恰好落在 ABCD的边所在的直线上时,求AP的长。
(1)、当AP为何值时?点Q与点B间的距离最小。(2)、若QB⊥CD,求AP的长。(3)、若点Q恰好落在 ABCD的边所在的直线上时,求AP的长。