浙江省温州市龙湾区2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-06-08 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分。共30分.）

1. 若要使式子 $\sqrt{3 - x}$ 有意义，则下列数值x不能取的是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 下列方程中，属于一元二次方程的是（）

A、x+y＝1 B、x²+x＝1 C、x+ $\frac{1}{x}$ ＝1 D、x³+x²＝1

查看试题解析
3. 计算 $\sqrt{12}$ ﹣ $\sqrt{3}$ 的结果是（）

A、 $\sqrt{3}$ B、3 C、 $\sqrt{9}$ D、±3

查看试题解析
4. 我市某一周每天的最高气温统计如下（单位：℃）：27，28，29，28，29，30，29，这一组数据的众数与中位数分别是（）

A、28，28 B、28，29 C、29，28 D、29，29

查看试题解析
5. 已知在▱ABCD中，∠A+∠C＝100°，则∠A等于（）

A、40° B、50° C、80° D、100°

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{9}$ ＝±3 B、 $\sqrt{2^{2} + 3^{2}}$ ＝5 C、 $\sqrt{12} \cdot \sqrt{\frac{1}{3}}$ =2 D、 $\sqrt{{(- 3)}^{2}}$ ＝﹣3

查看试题解析
7. 某校对学生一学期的各学科学业的总平均分是按如图所示的雨形图信息要求进行计算的已知该校八年级一班李明同学这个学期的数学成绩如下表：

李明

平时作业

期中考试

期末考试

90

85

88

则李明这个学期数学的总平均例为（）

A、87.5 B、87.6 C、87.7 D、87.8

查看试题解析
8. 关于x的一元二次方程x²﹣mx+m﹣2＝0的根的情况，下列说法正确的是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、与m的值有关，无法确定

查看试题解析
9. 已知实数x ， y满足（x²+y²）²﹣2（x²+y²）＝48，且xy＝2，则下列结论正确的是（）

A、x²+y²＝8或x²+y²＝﹣6 B、x﹣y＝2 C、x+y＝2 $\sqrt{3}$ D、x+y＝±2 $\sqrt{3}$

查看试题解析
10. 《周髀算经》中有一种几何方法可以用来解形如x（x+5）＝24的方程的正数解，方法为：如图，将四个长为x+5，宽为x的长方形纸片（面积均为24）拼成一个大正方形，于是大正方形的面积为：24×4+25＝121，边长为11，故得x（x+5）＝24的正数解为x＝ $\frac{11 - 5}{x}$ ，小明按此方法解关于x的方程x²+mx﹣n＝0时，构造出同样的图形．已知大正方形的面积为10，小正方形的面积为4，则（）

A、m＝2，n＝3 B、m＝ $\sqrt{10}$ ，n＝2 C、m＝ $\frac{5}{2}$ ，n＝2 D、m＝2，n＝ $\frac{3}{2}$

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分）

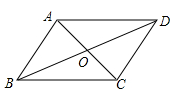
11. 当x＝3时，二次根式 $\sqrt{19 - x}$ 的值为．

查看试题解析
12. 已知一组数据2，3，4，5，6，x的众数为5，则这组数据的中位数为．

查看试题解析
13. 已知一个六边形的每个内角都相等，则它的其中一个内角的度数为．

查看试题解析
14. 比较大小： $\sqrt{15} + \sqrt{6}$ $\sqrt{13} + \sqrt{7}$ ．

查看试题解析
15. 如图，已知▱ABCD的周长是10，对角线AC与BD交于点O ， △AOD的周长比△AOB的周长多1，则AB的长为．

查看试题解析
16. 某校组织学生参加植树活动，活动结束后，统计了九年级甲班50名学生每人植树的情况，绘制了如下的统计表：

植树棵数

3

4

5

6

人数 20 15 10 5

那么这50名学生平均每人植树棵．

查看试题解析
17. 某种品牌手机经过4，5月份连续两次降价，每部售价由5000元降到3600元，且5月份降价的百分率是4月份降价的百分率的2倍．设4月份降价的百分率为x ，根据题意可列方程为．

查看试题解析
18. 如图，在▱ABCD中，∠A＝60°，E是AD上一点，连接BE ．将△ABE沿BE对折得到△A'BE ，当点A'恰好落在边AD上时，A'D＝2（图甲），当点A'恰好落在边CD上时，A'D＝3（图乙），则AB＝．

查看试题解析

三、解答题（本题有6小题，共46分．）

19. 计算：

(1)、 $\sqrt{8} - \sqrt{{(1 - \sqrt{2})}^{2}} + \sqrt{\frac{1}{2}}$ ；

(2)、（2 $\sqrt{3}$ + $\sqrt{2}$ ）² $- \sqrt{6}$ （ $\sqrt{6}$ +3）．

查看试题解析
20. 解方程：

(1)、x²+4x＝0；

(2)、（2x﹣1）²＝4x﹣2．

查看试题解析

21. 甲、乙两名射击运动员进行射击比赛，两人在相同条件下各射击5次，射击的成绩（单位：环）如下表所示：

	第一次	第二次	第三次	第四次	第五次
甲	10	6	8	10	6
乙	9	8	7	7	9

根据表中信息，解答下列问题：

(1)、甲的成绩的平均数是，乙的成绩的中位数是；

(2)、分别计算甲、乙两人成绩的方差，并从计算结果分析，哪位运动员的射击成绩更稳定？

查看试题解析

22. 如图，BD是▱ABCD的对角线，作AE⊥BD ， CF⊥BD ，垂足分别为E ， F ．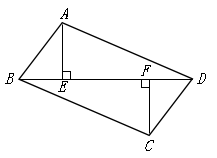

(1)、求证：AE＝CF；

(2)、若∠ABD＝45°，∠CBD＝30°，AB＝2，求▱ABCD的面积．

查看试题解析
23. 如图，将一张长方形纸板ABCD剪去四个边角（阴影部分）后制作成一个有盖的长方体纸盒（无缝衔接），在剪去的四个边角中，左侧两个是边长为5cm的正方形，右侧两个是有一边长为5cm的长方形，且AD＝2AB ，设AB＝xcm ．

(1)、请用含x的代数式分别表示长方体纸盒底面的长和宽：EH＝cm ， EF＝cm；

(2)、若所制作的长方体纸盒的容积为1500cm³ ，求长方体纸盒的表面积．

查看试题解析
24. 如图1，Rt△ABC中，∠ACB＝90，BC＝4，∠ABC＝60°，点P、Q是边AB ， BC上两个动点，且BP＝4CQ ，以BP ， BQ为邻边作平行四边形BPDQ ， PD ， QD分别交AC于点E ， F ，设CQ＝m ．

(1)、当平行四边形BPDQ的面积为6 $\sqrt{3}$ 时，求m的值；

(2)、求证：△DEF≌△QCF；

(3)、如图2，连接AD ， PF ， PQ ，当AD与△PQF的一边平行时，求△PQF的面积．

查看试题解析

李明	平时作业	期中考试	期末考试
李明	90	85	88

植树棵数	3	4	5	6
人数	20	15	10	5