浙江省杭州市滨江区2021年数学中考二模试卷

试卷更新日期：2021-06-08 类型：中考模拟

进入出卷网下载

一、选择题（本大题有10个小题，每小题3分，共30分）

1. 3的相反数是（）

A、﹣3 B、﹣ $\frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
2. 将一块直尺与一块三角板如图放置，若∠1＝45°，则∠2的度数为（）

A、145° B、135° C、120° D、115°

查看试题解析
3. 下列运算正确的是（）

A、2x+y＝2xy B、x²•x³＝x⁶ C、2x⁶÷x²＝2x⁴ D、4x﹣5x＝﹣1

查看试题解析
4. 在某次捐款活动中，80名爱心人士捐款金额（单位：元）如下表所示，这组数据中，中位数是（）

金额（元）

200

500

800

1000

频数

20

30

20

10

A、25 B、30 C、500 D、650

查看试题解析
5. 若x﹣y＜0，则（）

A、x﹣3＜y﹣3 B、2﹣x＜2﹣y C、 $\frac{x}{y}$ ＜0 D、x•y＞0

查看试题解析
6. 用一条长60cm的绳子怎样围成一个面积为200cm²的矩形？设矩形的一边为xcm ，根据题意，可列方程为（）

A、x（30+x）＝200 B、x（30﹣x）＝200 C、x（x+60）＝200 D、x（60﹣x）＝200

查看试题解析
7. 已知一次函数y₁＝ax+b ， y₂＝cx+d（a ， b ， c ， d均为常数，且a•c≠0）在平面直角坐标系中的图象如图所示，则（）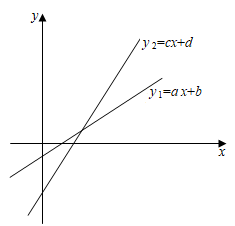

A、c＜a＜d＜b B、a＜c＜d＜b C、d＜b＜c＜a D、d＜b＜a＜c

查看试题解析
8. 如图，在△ABC中，以AB为直径作⊙O ，交AC于点E ，交BC于点D ，若CD＝BD ，则（）

A、AC＝BC B、 $\overset{⌢}{A E} = \overset{⌢}{B E}$ C、AB＝2DE D、BC•BD＝AB•CE

查看试题解析
9. 如图，在△ABC中，∠ACB＝90°，AB＝5，BC＝4，将△ABC沿BD折叠，使点C落在AB边上的点E处，过点E作EH∥AD ，交BD于点H ，过点H作HF⊥AB于点F ，则 $\frac{H E}{H F}$ ＝（）

A、 $\frac{4}{3}$ B、 $\frac{5}{4}$ C、 $\frac{5}{3}$ D、 $\frac{16}{15}$

查看试题解析
10. 在平面直角坐标系中，设函数y＝（x﹣4）（mx+4m﹣n）（m ， n为常数，且m≠0）（）

A、若y≥0恒成立，则8n﹣m＝0 B、若8n﹣m＝0，则y≤0恒成立 C、若y≤0恒成立，则8m﹣n＝0 D、若8m﹣n＝0，则 y≥0恒成立

查看试题解析

二、填空题（本大题有6个小题，每小题4分，共24分）

11. $\sqrt{4}$ = ．

查看试题解析
12. 分解因式：x³﹣xy²= ．

查看试题解析
13. 小红与小英一起玩“石头，剪刀，布”的游戏，则两位同学同时出“布”的概率是．

查看试题解析
14. 在Rt△ABC中，∠BAC＝90°，点G是△ABC的重心，如果AG＝8，那么BC的长为．

查看试题解析
15. 函数y₁＝（x+1）（x﹣2a）（a为常数）图像与x轴相交于点（x₁ ， 0）（x₂ ， 0），函数y₂＝x﹣a的图像与x轴相交于点（x₃ ， 0），若x₁＜x₃＜x₂ ，则a的取值范围为．

查看试题解析
16. 如图，在菱形ABCD中，点G在边CD上，∠DAG＝∠DBC ，且DG：CG＝2：3，则sin∠ABC＝．

查看试题解析

三、解答题（本大题有7个小题，共66分）

17. 解方程：x（x﹣5）＝5﹣x ．小滨的解答如下：
解：原方程可化简为x（x﹣5）＝﹣（x﹣5），

方程两边同时除以x﹣5，得x＝﹣1，

小滨的解答是否正确，如不正确，写出正确的解答过程．

查看试题解析

18. 某区为了解居民生活用水情况，通过随机抽样的方式对去年家庭户的月均用水量（单位：吨）进行调查，绘制了如下频数表和频数直方图：

分组	频数
2.0＜x≤3.5	11
3.5＜x≤5.0	a
5.0＜x≤6.5	13
6.5＜x≤8.0	b
8.0＜x≤9.5	2
合计	50

(1)、求a ， b的值，补全频数直方图．

(2)、为了鼓励节约用水，要确定一个月用水量的标准，超出这个标准的部分按1.8倍价格收费．若要使60%的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？

查看试题解析

19. 已知，如图，AB是⊙O的直径，直线DC ， DA分别切⊙O于点C ，点A ，连接BC ， OD ．

(1)、求证：BC∥OD；

(2)、若∠ODC＝35°，AB＝12，求出 $\overset{⌢}{B C}$ 的长．

查看试题解析
20. 用若根火柴首尾相接摆成一个矩形，设每一根火柴的长度为1，矩形两条邻边的长分别别为x ， y ，要求摆成的矩形的面积为8．

(1)、求y关于x的函数表达式；

(2)、能否摆成正方形？请说明理由．

查看试题解析
21. 如图，已知四边形ABCD是菱形，点E ， F ， G ， H分别在线段AB ， AD ， CD ， BC上，BE＝DF ， EG∥BC ， FH∥DC ， EG与FH相交于点P ．

(1)、求证：四边形HCGP是菱形．

(2)、若四边形BHPE是菱形，求证：点E是线段AB的中点．

查看试题解析
22. 在平面直角坐标系中，设二次函数y＝ax²﹣bx﹣a+b（a ， b为常数，且a≠0）．

(1)、当a＝1时，函数图象当对称轴为直线x＝2，求该函数当表达式．

(2)、求证：该函数图象一定经过一个定点．

(3)、若b﹣a＜0，点P（3，m）（m＜0）在该二次函数图象上，求证：a＜0．

查看试题解析
23. 如图，已知一条笔直的公路AB两侧有四所学校C ， D ， E ， G ，记学校C ， D ， E ， G到公路AB的距离分别为AC ， BD ， AE ， GH ．其中，学校C、E关于公路AB对称，学校G在BC与DE的交点处．

(1)、若AC＝6km ， BD＝12km ． ①求证：△CEG≌△BDG ． ②求GH的长．

(2)、求证： $\frac{1}{G H} - \frac{1}{A C} = \frac{2}{B D}$ ．

查看试题解析

金额（元）	200	500	800	1000
频数	20	30	20	10