浙江省宁波市镇海区2021年数学中考模拟试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 规定向右移动3个单位记作+3,那么向左移动2个单位记作( ).A、+2 B、-2 C、 D、2. 计算 的结果为( ).A、 B、 C、 D、3. 截止2021年3月9日,全球新冠肺炎累计确诊病例突破1亿1775万例,数1亿1775万用科学记数法可表示为( ).A、 B、 C、 D、4. 如图是一个直五棱柱,它的主视图正确的是( ).
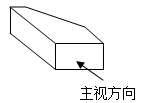 A、
A、 B、
B、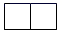 C、
C、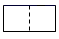 D、
D、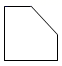 5. 有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )A、中位数 B、平均数 C、众数 D、方差6. 把一些书分给几名同学,若每人分10本,则多8本;若每人分11本,仍有剩余.依题意,设有 名同学,可列不等式( ).A、 B、 C、 D、7. 对于命题“如果 ,那么 ”,能说明它是假命题的是( ).A、 , B、 , C、 D、 ,8. 如图, 为 的切线,切点为A,连接 , 与 交于点C,延长 与 交于点D,连接 ,若 ,则 的度数为( )
5. 有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )A、中位数 B、平均数 C、众数 D、方差6. 把一些书分给几名同学,若每人分10本,则多8本;若每人分11本,仍有剩余.依题意,设有 名同学,可列不等式( ).A、 B、 C、 D、7. 对于命题“如果 ,那么 ”,能说明它是假命题的是( ).A、 , B、 , C、 D、 ,8. 如图, 为 的切线,切点为A,连接 , 与 交于点C,延长 与 交于点D,连接 ,若 ,则 的度数为( ) A、 B、 C、 D、9. 如图,已知二次函数 的图象与 轴交于点 、 ,且 ,与 轴交于正半轴.下列结论错误的是( ).
A、 B、 C、 D、9. 如图,已知二次函数 的图象与 轴交于点 、 ,且 ,与 轴交于正半轴.下列结论错误的是( ). A、 B、当 时, 随 增大而增大 C、当 时, 随 增大而减小 D、10. 如图,两个大小相同的正方形 , 如图放置,点 , 分别在边 , 上,若要求出阴影部分的周长,只要知道下列哪条线段的长度即可( ).
A、 B、当 时, 随 增大而增大 C、当 时, 随 增大而减小 D、10. 如图,两个大小相同的正方形 , 如图放置,点 , 分别在边 , 上,若要求出阴影部分的周长,只要知道下列哪条线段的长度即可( ).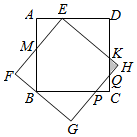 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:x3﹣4xy2= .12. 某路口红绿灯的时间设置为:红灯20秒,绿灯40秒,黄灯4秒.当人或车随意经过该路口时,遇到红灯的概率是.13. 如图,矩形 中, , , 与矩形的边 、 、 分别相切于点 、 、 ,点 是 上任意一点,则线段 长度的最小值为.
 14. 如图在圆心角为 的扇形 中,半径 ,以 为直径作半圆 .过点 作 的平行线交两弧分别于点 ,则图中阴影部分的面积是.
14. 如图在圆心角为 的扇形 中,半径 ,以 为直径作半圆 .过点 作 的平行线交两弧分别于点 ,则图中阴影部分的面积是.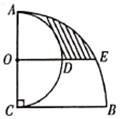 15. 如图,双曲线 ( 为常数, )与矩形 的边 相交于点 ,与边 相交于点 ,将 沿 翻折,点 恰好落在 轴上的点 处.则点 的坐标为.
15. 如图,双曲线 ( 为常数, )与矩形 的边 相交于点 ,与边 相交于点 ,将 沿 翻折,点 恰好落在 轴上的点 处.则点 的坐标为.
三、解答题
-
16.(1)、计算: .(2)、计算: .17. 如图,方格纸中的每个小正方形的边长都是1, 是格点三角形(顶点在方格顶点处).
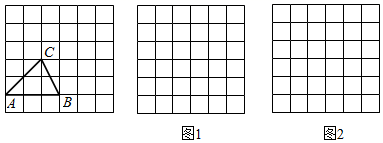 (1)、在图1中画出一个格点 ,使得 与 相似,周长之比为2:1;(2)、在图2中画出一个格点 ,使得 与 相似,面积之比为2:1.18. 某区组织学生参加党史知识竞赛,从中抽取了200名学生的成绩(得分取正整数,满分为100分)进行统计,根据成绩分成如下5组:
(1)、在图1中画出一个格点 ,使得 与 相似,周长之比为2:1;(2)、在图2中画出一个格点 ,使得 与 相似,面积之比为2:1.18. 某区组织学生参加党史知识竞赛,从中抽取了200名学生的成绩(得分取正整数,满分为100分)进行统计,根据成绩分成如下5组:A.
B.
C.
D.
E.
并绘制成如下两个统计图.
 (1)、求频数分布直方图中的 , 的值;(2)、在扇形统计图中, 组所对应扇形的圆心角为 ,求 的值;(3)、求 组共有多少人?(4)、该区共有1200名学生参加党史知识竞赛,如果设定获得一等奖的分数不低于91分,那么请你通过计算估计全区获得一等奖的人数是多少?19. 如图,已知 和 均是直角三角形, , , 于点 .
(1)、求频数分布直方图中的 , 的值;(2)、在扇形统计图中, 组所对应扇形的圆心角为 ,求 的值;(3)、求 组共有多少人?(4)、该区共有1200名学生参加党史知识竞赛,如果设定获得一等奖的分数不低于91分,那么请你通过计算估计全区获得一等奖的人数是多少?19. 如图,已知 和 均是直角三角形, , , 于点 . (1)、求证: ≌ ;(2)、若点 是 的中点, ,求 的长.20. 如图,在一次足球比赛中,守门员在地面 处将球踢出,一运动员在离守门员8米的 处发现球在自己头上的正上方4米处达到最高点 ,球落地后又一次弹起.据实验测算,足球在空中运行的路线是一条抛物线,在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)、求证: ≌ ;(2)、若点 是 的中点, ,求 的长.20. 如图,在一次足球比赛中,守门员在地面 处将球踢出,一运动员在离守门员8米的 处发现球在自己头上的正上方4米处达到最高点 ,球落地后又一次弹起.据实验测算,足球在空中运行的路线是一条抛物线,在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半. (1)、求足球第一次落地之前的运动路线的函数表达式及第一次落地点 和守门员(点 )的距离;(2)、运动员(点 )要抢到第二个落点 ,他应再向前跑多少米?(假设点 、 、 、 在同一条直线上,结果保留根号)21. 某公司销售甲、乙、丙三种型号的器材.3月份公司需支付的工资 (万元)和其余开支 (万元)与总销售量 的关系如图所示.
(1)、求足球第一次落地之前的运动路线的函数表达式及第一次落地点 和守门员(点 )的距离;(2)、运动员(点 )要抢到第二个落点 ,他应再向前跑多少米?(假设点 、 、 、 在同一条直线上,结果保留根号)21. 某公司销售甲、乙、丙三种型号的器材.3月份公司需支付的工资 (万元)和其余开支 (万元)与总销售量 的关系如图所示.
型号
甲
乙
丙
进价(万元/台)
0.9
0.2
1.1
售价(万元/台)
1.2
1.6
1.3
(1)、求 与 的函数关系式;(2)、若3月份该公司需支付的工资和其余开支共3.8万元,求出这个月三种器材的总销售量;(3)、在(2)的条件下,若3月份公司共花64万元购进甲、乙、丙三种器材,并保证全部卖出.这三种器材的进价和售价如右上表所示,若3月份的总销售利润为16.2万元,请求出甲、乙、丙三种器材各卖出几台?(总销售利润=销售总价-总进价-工资-其余开支)22. 如图,如果一个矩形 绕点 逆时针方向旋转 得到矩形 , 为对角线 中点,若边 与边 恰好交于点 ,我们称这样的旋转为有效旋转.此时边 与边 交于点 .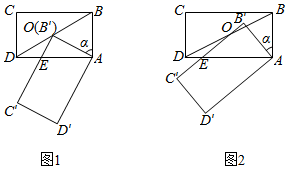 (1)、如图1,如果矩形 经过有效旋转后,点 与 恰好重合,求 的值.(2)、如图2,如果矩形 经过有效旋转后,点 与 不重合.
(1)、如图1,如果矩形 经过有效旋转后,点 与 恰好重合,求 的值.(2)、如图2,如果矩形 经过有效旋转后,点 与 不重合.①判断 是否为定值,并说明理由;
②若 , ,求 的长.
23. 已知 ,经过点 、 作圆交 边于点 ,交 边于点 ,点 是圆内一点,且满足 , ,连结 和 交于点 . (1)、求证: ∽ ;(2)、探索 和 的位置关系,并说明理由;(3)、若 ,且 ,
(1)、求证: ∽ ;(2)、探索 和 的位置关系,并说明理由;(3)、若 ,且 ,①当 时,求 的长度;
②当 最小时,请直接写出 的值.