浙江省宁波市余姚市2021年数学中考一模试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、选择题(每小题4分,共40分.)
-
1. ﹣2021的绝对值是( )A、2021 B、 C、﹣ D、﹣20212. 下列运算正确的是( )A、(a+b)2=a2+b2 B、(﹣3x3)2=6x6 C、a2+a2=2a4 D、(a4)3=a123. 近年来,华为手机越来越受到消费者的青睐.2020年第三季度,华为手机销量为2880万部.将2880万用科学记数法表示为( )A、288×105 B、2.88×108 C、2.88×107 D、2.88×1064. 下列说法正确的是( )A、为了解三名学生的视力情况,采用抽样调查 B、“任意画一个三角形,其内角和是360°”是必然事件 C、要调查某班同学最喜爱的文艺节目,应该关注的统计量是众数 D、小聪和小明最近5次数学测验成绩的平均分和方差分别为 =82分, =82分,S小聪2=245分2 , S小明2=90分2 , 则小聪的数学成绩较为稳定5. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、
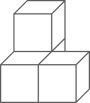 B、
B、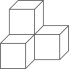 C、
C、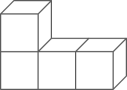 D、
D、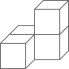 6. 如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是( )
6. 如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是( ) A、135° B、120° C、115° D、105°7. 我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,两车空出来;每车坐2人,多出9人无车坐.问人数和车数各多少?设车x辆,根据题意,可列出的方程是( )A、3x﹣2=2x+9 B、3(x﹣2)=2x+9 C、 D、3(x﹣2)=2(x+9)8. 如图,四边形ABCD的顶点B,C,D都在⊙A上,AD∥BC,∠BAD=140°,AC=3,则 的弧长为( )
A、135° B、120° C、115° D、105°7. 我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,两车空出来;每车坐2人,多出9人无车坐.问人数和车数各多少?设车x辆,根据题意,可列出的方程是( )A、3x﹣2=2x+9 B、3(x﹣2)=2x+9 C、 D、3(x﹣2)=2(x+9)8. 如图,四边形ABCD的顶点B,C,D都在⊙A上,AD∥BC,∠BAD=140°,AC=3,则 的弧长为( ) A、 π B、 π C、 π D、 π9. 已知二次函数y=a(x﹣m)2(a>0)的图象经过点A(﹣1,p),B(3,q),且p<q,则m的值不可能是( )A、﹣2 B、﹣ C、0 D、10. 如图,点P,Q,R分别在等边△ABC的三边上,且AP=BQ=CR,过点P,Q,R分别作BC,CA,AB边的垂线,得到△DEF.若要求△DEF的面积,则只需知道( )
A、 π B、 π C、 π D、 π9. 已知二次函数y=a(x﹣m)2(a>0)的图象经过点A(﹣1,p),B(3,q),且p<q,则m的值不可能是( )A、﹣2 B、﹣ C、0 D、10. 如图,点P,Q,R分别在等边△ABC的三边上,且AP=BQ=CR,过点P,Q,R分别作BC,CA,AB边的垂线,得到△DEF.若要求△DEF的面积,则只需知道( ) A、AB的长 B、AP的长 C、BP的长 D、DP的长
A、AB的长 B、AP的长 C、BP的长 D、DP的长二、填空题(每小题5分,共30分}
-
11. 分解因式:x2﹣6x+9= .12. 若 在实数范围内有意义,则x的取值范围是.13. 一个布袋里装有只有颜色不同的3个球,其中2个红球,1个白球.从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则摸出的2个球都是红球的概率是.14. 已知x=﹣1是一元二次方程ax2+bx﹣10=0的一个解,且a≠﹣b,则 的值为 .15. 如图,△ABC中,∠ACB=90°,AC=BC,点D在AB的延长线上,且BD=AB,连接DC并延长,作AE⊥CD于E.若AE= ,则△BCD的面积为.
 16. 如图,一次函数y=﹣ 与反比例函数y= 的图象交于A、B两点,与y轴交于C点.若OC=OA,△ABO的面积为5.则∠CAO的正切值为 , k的值为.
16. 如图,一次函数y=﹣ 与反比例函数y= 的图象交于A、B两点,与y轴交于C点.若OC=OA,△ABO的面积为5.则∠CAO的正切值为 , k的值为.
三、解答题(本大题有8小题,共80分)
-
17.(1)、化简:a(a﹣2)﹣(a+2)(a﹣2).(2)、解不等式: ≤3x+5.18. 如图,由24个边长为1的小正方形组成的6×4的网格中,△ABC的顶点都在格点(小正方形的顶点)上.请在所给的网格中分别画一条线段DE,并同时满足如下条件:
①点D,E分别在BC,AC边上.
②点D,E都是格点.
③图1中满足DE= AB,图2中满足DE= AC.
 19. 某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集并整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图.请根据图中的信息解答下列问题:
19. 某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集并整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图.请根据图中的信息解答下列问题: (1)、求该校九年级接受调查的人数并补全条形统计图.(2)、计算扇形统计图中的“体育活动”所对应的圆心角度数.(3)、若该校九年级有450名学生,请估计该校九年级学生中喜欢“听音乐”方式进行考前减压的人数.20. 为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温(如图1),其红外线探测点O可以在垂直于地面的支杆OP上下调节(如图2),已知探测最大角(∠OBC)为58.0°,探测最小角(∠OAC)为26.6°.
(1)、求该校九年级接受调查的人数并补全条形统计图.(2)、计算扇形统计图中的“体育活动”所对应的圆心角度数.(3)、若该校九年级有450名学生,请估计该校九年级学生中喜欢“听音乐”方式进行考前减压的人数.20. 为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温(如图1),其红外线探测点O可以在垂直于地面的支杆OP上下调节(如图2),已知探测最大角(∠OBC)为58.0°,探测最小角(∠OAC)为26.6°. (1)、若该设备的安装高度OC为1.6米时,求测温区域的宽度AB.(2)、该校要求测温区域的宽度AB为2.53m,请你帮助学校确定该设备的安装高度OC.
(1)、若该设备的安装高度OC为1.6米时,求测温区域的宽度AB.(2)、该校要求测温区域的宽度AB为2.53m,请你帮助学校确定该设备的安装高度OC.(结果精确到0.01m,参考数据:sin58.0°≈0.85,cos58.0°≈0.53,tan58.0°≈1.60,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)
21. 如图,已知二次函数y= x2﹣x+c的图象经过点P(﹣3,6). (1)、求该二次函数的表达式.(2)、求该二次函数图象的顶点坐标.(3)、点Q(m,n)在该二次函数图象上,若点Q到y轴的距离小于3.请根据图象直接写出n的取值范围.22. A.B两地相距200千米,早上8:00货车从A地出发将一批防疫物资运往B地,出发1.6小时后,货车出现了故障.货车离开A地的路程y(km)与时间x(h)的函数关系如图所示.
(1)、求该二次函数的表达式.(2)、求该二次函数图象的顶点坐标.(3)、点Q(m,n)在该二次函数图象上,若点Q到y轴的距离小于3.请根据图象直接写出n的取值范围.22. A.B两地相距200千米,早上8:00货车从A地出发将一批防疫物资运往B地,出发1.6小时后,货车出现了故障.货车离开A地的路程y(km)与时间x(h)的函数关系如图所示. (1)、求货车刚出发时候的速度.(2)、若货车司机经过48分钟维修排除了故障,继续运送物资赶往B地.
(1)、求货车刚出发时候的速度.(2)、若货车司机经过48分钟维修排除了故障,继续运送物资赶往B地.①应防疫需要,现要求该批次物资运到B地的时间不迟于当天中午12:00,那么货车的速度至少应该提速到多少?
②在货车从A地出发半小时后,A地派出了30名医务人员乘坐大巴车前往B地进行医疗支援.若货车在排除故障后以①中所求速度的最小值匀速赶往B地,大巴车的速度为50km/h.求大巴车在行进途中与货车相遇时,离B地还有多少千米?
23. 如果等腰三角形一边上的高线长恰好等于这边的长,那么称这个三角形为“优美三角形”,这条边为“优美边”. (1)、在如图1所示的12个小正方形组成的网格中,A,B两点在小正方形的顶点上,若点C也在小正方形的顶点上,且△ABC是“优美三角形”,请在图中各画一个满足条件的△ABC,并直接写出∠ABC的正切值.(2)、如图2,已知四边形ABCD是菱形,∠BAD=2α,点P,Q同时从B,D出发以相同的速度向终点C运动.
(1)、在如图1所示的12个小正方形组成的网格中,A,B两点在小正方形的顶点上,若点C也在小正方形的顶点上,且△ABC是“优美三角形”,请在图中各画一个满足条件的△ABC,并直接写出∠ABC的正切值.(2)、如图2,已知四边形ABCD是菱形,∠BAD=2α,点P,Q同时从B,D出发以相同的速度向终点C运动.①当tanα=2,△APQ是“优美三角形”,且PQ为“优美边”时,求 的值.
②试探究P,Q在运动过程中(不含起点),tanα的范围与△APQ是“优美三角形”的个数之间的关系(不需要说明理由).
24. 如图1,在平面直角坐标系中,点A的坐标为(﹣2,2),B是x轴正半轴上一动点,以AB为直径画⊙C交x轴于点D,连接AO,过点A作AE⊥AO交⊙C于点E,连接BE,DE. (1)、求∠DBE的度数.(2)、求证:△ADE∽△OAB.(3)、如图2,连接CE,过点C作CF⊥BE于点F,过点F作FG∥CE交DE的延长线于点G,设点B的横坐标为t.
(1)、求∠DBE的度数.(2)、求证:△ADE∽△OAB.(3)、如图2,连接CE,过点C作CF⊥BE于点F,过点F作FG∥CE交DE的延长线于点G,设点B的横坐标为t.①用含t的代数式表示DE2.
②记S=DE•EG,求S关于t的函数表达式.