浙江省杭州市西湖区2021年数学中考一模试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、选择题:本大题有10个小题,每小题3分,共30分。
-
1. × =( )A、2 B、4 C、2+ D、22. (m+2)(m﹣2)=( )A、m2+4 B、m2﹣4 C、m2+2 D、m2﹣23. 某文具店一本练习本和一支水笔的单价合计为3元,小妮在该店买了20本练习本和10支水笔,共花了36元.如果设练习本每本为x元,水笔每支为y元,那么根据题意,下列方程组中,正确的是( )
A、 B、 C、 D、4. 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,如果∠EFG=64°,那么∠EGD的大小是( ) A、122° B、124° C、120° D、126°5. 某校七年级学生的平均年龄为13岁,年龄的方差为3,若学生人数没有变动,则两年后的同一批学生,对其年龄的说法正确的是( )A、平均年龄为13岁,方差改变 B、平均年龄为15岁,方差不变 C、平均年龄为15岁,方差改变 D、平均年龄为13岁,方差不变6. 已知点P(1,m),Q(2,n)是反比例函数y= 图象上的两点,则( )A、m<n<0 B、n<m<0 C、0<m<n D、0<n<m7. 如图,AB是⊙O的直径,CD是弦,若∠CDB=26°,则∠ABC=( )
A、122° B、124° C、120° D、126°5. 某校七年级学生的平均年龄为13岁,年龄的方差为3,若学生人数没有变动,则两年后的同一批学生,对其年龄的说法正确的是( )A、平均年龄为13岁,方差改变 B、平均年龄为15岁,方差不变 C、平均年龄为15岁,方差改变 D、平均年龄为13岁,方差不变6. 已知点P(1,m),Q(2,n)是反比例函数y= 图象上的两点,则( )A、m<n<0 B、n<m<0 C、0<m<n D、0<n<m7. 如图,AB是⊙O的直径,CD是弦,若∠CDB=26°,则∠ABC=( ) A、26° B、52° C、64° D、74°8. 平面直角坐标系中,已知函数y=ax+b(a>0,b<0)的图象经过点P(1,3),则该函数的图象可能是( )A、
A、26° B、52° C、64° D、74°8. 平面直角坐标系中,已知函数y=ax+b(a>0,b<0)的图象经过点P(1,3),则该函数的图象可能是( )A、 B、
B、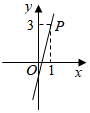 C、
C、 D、
D、 9. 如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( )
9. 如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( ) A、3α+β=180° B、2α+β=180° C、3α﹣β=90° D、2α﹣β=90°10. 已知m,n是非零实数,设k= = ,则( )A、k2=3﹣k B、k2=k﹣3 C、k2=﹣3﹣k D、k2=k+3
A、3α+β=180° B、2α+β=180° C、3α﹣β=90° D、2α﹣β=90°10. 已知m,n是非零实数,设k= = ,则( )A、k2=3﹣k B、k2=k﹣3 C、k2=﹣3﹣k D、k2=k+3二、填空题:本大题有6个小题,每小题4分,共24分.
-
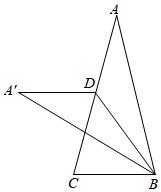
11. 计算tan45°=.12. 矩形ABCD中,A(﹣3,2),B(0,2),C(0,3),则点D坐标为.13. 如果从长度分别为2、4、6、7的四条线段中随机抽取三条线段,那么抽取的三条线段能构成三角形的概率是 .14. 已知⊙O的半径为5cm,一条弦的弦心距为3cm,则此弦的长为cm.15. 小明用50元钱购买矿泉水和冰淇淋,每瓶矿泉水2元,每支冰淇淋6元,他买了6瓶矿泉水和若干支冰淇淋,则小明最多能买支冰淇淋.16. 如图,△ABC中,AB=AC,∠A=30°,点D在边AC上,将△ABD沿BD翻折,点A的对称点为A',使得A'D∥BC,则∠BDC= , =.
三、解答题:本大题有7个小题,共66分.
-
17. 如图
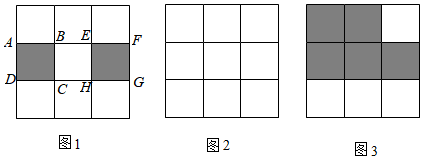 (1)、如图1,在3×3的方格中,正方形ABCD,EFGH的边长均为1.求出正方形ABCD的对角线AC的长,并将正方形ABCD,EFGH剪拼成一个大正方形,在图2中画出示意图.(2)、如图3,有5个小正方形(阴影部分),能剪拼成一个大正方形吗?若能,求出大正方形的边长;若不能,请说明理由.18. 如图是某厂对一批电灯泡的使用寿命进行检测后得到的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
(1)、如图1,在3×3的方格中,正方形ABCD,EFGH的边长均为1.求出正方形ABCD的对角线AC的长,并将正方形ABCD,EFGH剪拼成一个大正方形,在图2中画出示意图.(2)、如图3,有5个小正方形(阴影部分),能剪拼成一个大正方形吗?若能,求出大正方形的边长;若不能,请说明理由.18. 如图是某厂对一批电灯泡的使用寿命进行检测后得到的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).组别(时)
频数
400~450
20
450~500
m
500~550
30
550~600
10
 (1)、求m的值.(2)、若一个电灯泡亮一小时耗电0.1度,则这批电灯泡的总耗电量会超过5200度吗?说明理由.19. 如图,在正方形ABCD中,点E为对角线AC,BD交点,AF平分∠DAC交BD于点G,交DC于点F.
(1)、求m的值.(2)、若一个电灯泡亮一小时耗电0.1度,则这批电灯泡的总耗电量会超过5200度吗?说明理由.19. 如图,在正方形ABCD中,点E为对角线AC,BD交点,AF平分∠DAC交BD于点G,交DC于点F. (1)、求证:△AEG∽△ADF.(2)、判断△DGF的形状.(3)、若AG=1,求GF的长.20. 已知一次函数y=k(x﹣3)(k≠0).(1)、求证:点(3,0)在该函数图象上.(2)、若该函数图象向上平移2个单位后过点(4,﹣2),求k的值.(3)、若k<0,点A(x1 , y1),B(x2 , y2)在函数图象上,且y1<y2 , 判断x1﹣x2<0是否成立?请说明理由.21. 如图,△ABC中,AB=AC,∠BAC=30°,将△ABC绕着点A逆时针旋转30°,点C的对应点为点D,AD的延长线与BC的延长线相交于点E.
(1)、求证:△AEG∽△ADF.(2)、判断△DGF的形状.(3)、若AG=1,求GF的长.20. 已知一次函数y=k(x﹣3)(k≠0).(1)、求证:点(3,0)在该函数图象上.(2)、若该函数图象向上平移2个单位后过点(4,﹣2),求k的值.(3)、若k<0,点A(x1 , y1),B(x2 , y2)在函数图象上,且y1<y2 , 判断x1﹣x2<0是否成立?请说明理由.21. 如图,△ABC中,AB=AC,∠BAC=30°,将△ABC绕着点A逆时针旋转30°,点C的对应点为点D,AD的延长线与BC的延长线相交于点E. (1)、求∠B的度数.(2)、当AB=4时,求点B到AC的距离.(3)、若DE= ,求CE的长.22. 已知二次函数y1=x2+ax+1,y2=ax2+bx+1(a,b为常数,a≠0).(1)、若a=﹣2,求二次函数y1的顶点坐标.(2)、若b=4a,设函数y2的对称轴为直线x=k,求k的值.(3)、点P(x0 , m)在函数y1图象上,点Q(x0 , n)在函数y2图象上.若函数y1图象的对称轴在y轴右侧,当0<x0<1,b=1时,试比较m,n的大小.23. 如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)、求∠B的度数.(2)、当AB=4时,求点B到AC的距离.(3)、若DE= ,求CE的长.22. 已知二次函数y1=x2+ax+1,y2=ax2+bx+1(a,b为常数,a≠0).(1)、若a=﹣2,求二次函数y1的顶点坐标.(2)、若b=4a,设函数y2的对称轴为直线x=k,求k的值.(3)、点P(x0 , m)在函数y1图象上,点Q(x0 , n)在函数y2图象上.若函数y1图象的对称轴在y轴右侧,当0<x0<1,b=1时,试比较m,n的大小.23. 如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD. (1)、求证:△ACE≌△BCD.(2)、若CD=2,BD=3 ,求⊙O的半径.(3)、若点F为DE的中点,连接CF,FO,设CD=a,BD=b,求CF+FO.(用含有a,b的代数式表示)
(1)、求证:△ACE≌△BCD.(2)、若CD=2,BD=3 ,求⊙O的半径.(3)、若点F为DE的中点,连接CF,FO,设CD=a,BD=b,求CF+FO.(用含有a,b的代数式表示)