重庆市沙坪坝区2021年数学中考适应性试卷
试卷更新日期：2021-06-08 类型：中考模拟
一、单选题
-
1. ﹣2的绝对值是（ ）A、2 B、 C、 D、-22. 2020年12月7日，位于沙坪坝磁器口金碧正街的“重庆1949”大剧院顺利封顶，总建筑面积达23000平方米，其中数据23000用科学记数法表示为（ ）A、 23×103 B、2.3×103 C、2.3×104 D、0.23×1053. 4的平方根是（ ）A、 16 B、±2 C、2 D、-24. 下列长度的线段中，与长度为3，5的两条线段能组成三角形的是（ ）A、2 B、7 C、9 D、115. 把小正方形按如图所示的规律拼图案，图1中有1个小正方形，图2中有7个小正方形，图3中有13个小正方形，…，按此规律，则图6中小正方形的个数是（ ）
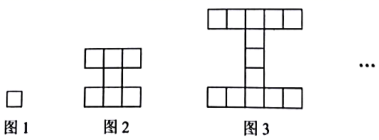A、25 B、28 C、31 D、376. 如图，AB是⊙O的切线，点B为切点，连接AO并延长交⊙O于点C，连接BC.若∠A＝26°，则∠C的度数为（ ）
A、26° B、32° C、52° D、64°7. 用配方法解方程x2+4x+1=0，配方后的方程是（ ）A、（x﹣2）2=5 B、（x+2）2=5 C、（x+2）2=3 D、（x﹣2）2=38. 如图，在平面直角坐标系中，△ABC与△DEF是以坐标原点O为位似中心的位似图形，若A（﹣2，0），D（3，0），且BC＝3，则线段EF的长度为（ ）
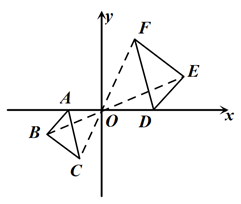A、2 B、4 C、 D、69. 某数学兴趣小组在歌乐山森林公园借助无人机测量某山峰的垂直高度AB.如图所示，无人机在地面BC上方120米的D处测得山顶A的仰角为22°，测得山脚C的俯角为63.5°.已知AC的坡度为1：0.75，点A，B，C，D在同一平面内，则山峰的垂直高度AB约为（ ）（参考数据：sin63.5°≈0.89，tan63.5°≈2.00，sin22°≈0.37，tan22°≈0.40）
A、141.4米 B、188.6米 C、205.7米 D、308.6米10. 若关于x的不等式组 无解，且关于y的分式方程 ＝1﹣ 的解为非负整数，则符合条件的所有整数a的和为（ ）A、0 B、16 C、18 D、2011. 某工厂中标生产一批型号相同的新能源汽车配件的定单，该工厂把定单任务平均分给了两车间，两车间每天都按各自的生产速度同时进行生产，中途因工厂同时对两车间设备进行检修维护，两车间停产4天后又各自按原来的速度进行生产，该工厂未完成的定单任务量y（件）与生产时间x（天）之间的函数关系如图所示.下列结论：①其中一个车间24天完成生产任务；②两车间生产速度之差是200件/天；③该工厂定单任务是24000件；④该工厂34天完成定单任务.其中正确的个数是（ ）
A、1 B、2 C、3 D、412. 如图，在矩形ABCD中，EF垂直平分AC，交BC于点E，连接DE，将△DEC沿直线DE翻折得到△DEM，EM与AD相交于点N.若AB＝3，BC＝3 ，则点A到直线EM的距离为（ ）
A、 B、 C、 D、二、填空题
-
13. 计算：（π﹣2021）0+（ ）﹣1＝.14. 如图，数轴上有三个点A，B，C，若点A，B表示的数互为相反数，且AB＝4，则点C表示的数是.
15. 在初中阶段共有6本不同的数学教材，把它们打乱顺序放进不透明的书包里，从书包里随机取出两本数学教材，恰好是同一年级的数学教材的概率是.16. 如图，在边长为 的正方形ABCD中，分别以四个顶点为圆心，以边长为半径画弧，分别与正方形的边和对角线相交，则图中阴影部分的面积为（结果保留π）.
17. 如图，在平面直角坐标系中，菱形ABCD的对角线AC，BD的交点与坐标原点O重合，AB与x轴交于点E，反比例函数y＝ （k＞0，x＞0）的图象经过点D.若点C（3，﹣6），E（﹣6，0），则k的值为.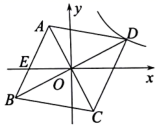
18. 磁器口古镇正在创建国家5A级景区，某门店积极响应号召，将A、B、C三种茶具以甲、乙、丙三种礼盒方式进行销售宣传.甲礼盒含有A茶具1个，B茶具2个，C茶具5个，乙礼盒含有A茶具1个，B茶具1个，C茶具2个，丙礼盒含有A茶具1个，B茶具3个，C茶具4个，甲、乙、丙三种礼盒均需相同的礼盒包装费用，且每个C茶具成本是每个B茶具成本的 ，甲、乙两种礼盒总成本之比是3：2，并将甲、乙、丙三种礼盒均以利润率50%进行定价销售.在今年元旦节当天，甲、乙两种礼盒均打8折销售且销量相同，丙礼盒打9折销售，甲、乙、丙三种礼盒总利润率达到23%，则今年元旦节当天丙礼盒销量与总销量之比为.（利润率＝ ×100%）三、解答题
-
19. 计算：(1)、x（y﹣4x）+（2x+y）（2x﹣y）；(2)、 ÷（1﹣ ）.20. 如图，在▱ABCD中，AB＝AC，∠B＝50°.
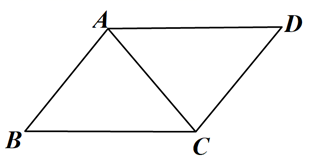(1)、使用直尺和圆规，作∠DAC的平分线AE交CD于点F（保留作图痕迹）；(2)、在（1）的条件下，求∠AFC的度数.21. 传承爱国情怀，讴歌百年党史，某校开展了“学党史，知党恩，跟党走”的知识竞赛，现从该校七、八年级中各随机抽取20名学生的竞赛成绩（100分制，80分及以上为优秀）进行整理、描述和分析（成绩用x表示，共分成四组：A.0≤x＜60，B.60≤x＜80，C.80≤x＜100，D.x＝100），下面给出了部分信息：七年级抽取的学生竞赛成绩在C组的数据是：80，84，85，90，95，98.
八年级抽取的学生竞赛成绩在C组的数据是：80，82，84，86，86，90，94，98.
年级
平均数
众数
中位数
满分率
七年级
82
100
b
25%
八年级
82
a
88
c
根据以上信息，解答下列问题：
(1)、直接写出a，b，c的值；(2)、根据上述数据，你认为该校七、八年级中哪个年级学生对“党史”掌握较好？请说明理由（写出一条理由即可）(3)、该校七、八年级共有800人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀的学生人数是多少？22. 探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程，以下是我们研究函数y＝| |的性质及其应用的部分过程，请按要求完成下列各小题：
(1)、请直接写出表中m，n的值，并在图中补全该函数图象；x
⋯
﹣5
﹣4
﹣3
﹣2
﹣1
0
1
3
4
5
6
7
⋯
y＝| |
⋯
m
0
2
6
6
n
3
⋯
(2)、结合函数图象，直接写出该函数的一条性质；(3)、已知函数y＝ 的图象如图所示，结合你所画的函数图象，直接写出不等式 的解集（保留1位小数，误差不超过0.2）.23. 中国新冠疫苗研发成功，举世瞩目，疫情得到有效控制，国内旅游业也逐渐回温，我市某酒店有A、B两种房间，A种房间房价每天200元，B种房间房价每天300元，今年2月，该酒店登记入住了120间，总营业收入28000元.(1)、求今年2月该酒店A种房间入住了多少间？(2)、该酒店为提高房间入住量，增加营业收入，大力借助网络平台进行宣传，同时将A种房间房价调低2a元，将B种房间房价下调a%，由此，今年3月，该酒店吸引了大批游客入住，A、B两种房间入住量都比2月增加了 a%，总营业收入在2月的基础上增加了a%，求a的值.24. 一个三位数的百位数字为a，十位数字为b，个位数字为c，若关于x的方程ax＝b的解是x＝c，则称这个三位数是方程ax＝b的“协调数”，称方程ax＝b是这个三位数的“协调方程”.如：三位数200，方程2x＝0的解是x＝0，所以200就是方程2x＝0的“协调数”，方程2x＝0是这个三位数200的“协调方程”.请根据上述材料，解决下列问题：
(1)、判断263是否是某个方程的“协调数”？方程2x＝7是否是某个三位数的“协调方程”？并说明理由；(2)、若所有的“协调数”的个数为s，所有“协调方程”的解之和为t，求s+t的值.25. 如图，在平面，在平面直角坐标系中，地物线y＝ x2+bx+c与x轴交于点A（﹣1，0），B（3，0）与y轴交于点C.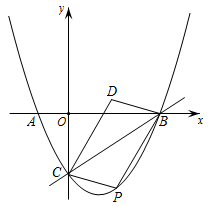
(1)、求该抛物线的函数表达式；(2)、点P是直线BC下方抛物线上的任意一点，连接PB，PC，以PB，PC为邻边作平行四边形CPBD，求四边形CPBD面积的最大值；(3)、将该抛物线沿射线CB方向平移 个单位，平移后的抛物线与y轴交于点E，点M为直线BC上的一点，在平面直角坐标系中是否存在点N，使以点C，E，M，N为顶点的四边形为矩形，若存在，请直接写出点N的坐标；若不存在，请说明理由.26. 如图，在锐角△ABC中，∠ACB＝45°，点D是边BC上一动点，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接DE交AC于点F.
(1)、如图1，若∠ADC＝60°，求证：DF＝AF+EF；(2)、如图2，在点D运动的过程中，当∠ADC是锐角时，点M在线段DC上，且AM＝AD，连接ME，猜想线段ME，MD，AC之间存在的数量关系，并证明你猜想的结论；(3)、在点D运动的过程中，当∠ADC是钝角时，点N是线段DE上一动点，连接CN，若CF＝ AF＝m，请直接用含m的代数式表示2CN+ NE的最小值.