重庆市九龙坡区2021年数学中考模拟试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、﹣1 D、2. 下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图所示的几何体的从左面看到的图形为( )
3. 如图所示的几何体的从左面看到的图形为( )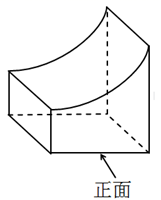 A、
A、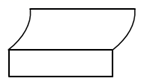 B、
B、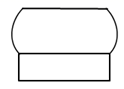 C、
C、 D、
D、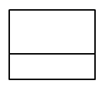 4. 计算(﹣0.25)2019•42020的结果为( )A、4 B、﹣4 C、 D、5. 下列说法正确的是( )A、相似多边形都是位似多边形 B、有一个角是100°的两个等腰三角形一定相似 C、两边对应成比例,且有一个角对应相等的两个三角形一定相似 D、所有的菱形都相似6. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则⊙O的半径为( )
4. 计算(﹣0.25)2019•42020的结果为( )A、4 B、﹣4 C、 D、5. 下列说法正确的是( )A、相似多边形都是位似多边形 B、有一个角是100°的两个等腰三角形一定相似 C、两边对应成比例,且有一个角对应相等的两个三角形一定相似 D、所有的菱形都相似6. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则⊙O的半径为( )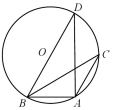 A、4 B、6 C、8 D、127. 按如图所示的程序计算,若开始输入的数为 ,则最后输出的结果是( )
A、4 B、6 C、8 D、127. 按如图所示的程序计算,若开始输入的数为 ,则最后输出的结果是( )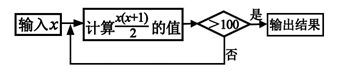 A、15 B、30 C、105 D、1208. 若 是方程 的两个实数根,则代数式 的值等于( )A、2020 B、2019 C、2029 D、20289. 山城重庆的美景吸引了很多游客,越来越多的人喜欢用无人机拍摄网红景点.如图,为了拍摄坡比为1:2.4的斜坡AB上的景点A,航拍无人机先从C点俯拍,此时的俯角为37°,为取得更震撼的拍摄效果,无人机升高100米到达D点,此时的俯角变为45°.已知坡AB的长为65米,则无人机与斜坡AB的坡底B的水平距离BE的长度为( )米.(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
A、15 B、30 C、105 D、1208. 若 是方程 的两个实数根,则代数式 的值等于( )A、2020 B、2019 C、2029 D、20289. 山城重庆的美景吸引了很多游客,越来越多的人喜欢用无人机拍摄网红景点.如图,为了拍摄坡比为1:2.4的斜坡AB上的景点A,航拍无人机先从C点俯拍,此时的俯角为37°,为取得更震撼的拍摄效果,无人机升高100米到达D点,此时的俯角变为45°.已知坡AB的长为65米,则无人机与斜坡AB的坡底B的水平距离BE的长度为( )米.(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80) A、335 B、340 C、345 D、35010. 如果关于x的不等式组 有且只有三个奇数解,且关于x的分式方程 有整数解,则符合条件的整数m有( )个A、1 B、2 C、3 D、411. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 (千米)与甲车行驶的时间 (小时)之间的函数关系如图所示,则下列结论:① , 两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时, 或 ,其中正确的结论有( )
A、335 B、340 C、345 D、35010. 如果关于x的不等式组 有且只有三个奇数解,且关于x的分式方程 有整数解,则符合条件的整数m有( )个A、1 B、2 C、3 D、411. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 (千米)与甲车行驶的时间 (小时)之间的函数关系如图所示,则下列结论:① , 两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时, 或 ,其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个12. 如图,在第一象限内,动点P在反比例函数y= 的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y= 的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
A、1个 B、2个 C、3个 D、4个12. 如图,在第一象限内,动点P在反比例函数y= 的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y= 的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个① 为定值;②若k=4m,则A为OP中点;③S△PEB= ;④OA2+PB2=PQ2.
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 人的血管首尾相连的长度大约可达96000千米,96000千米用科学记数法表示为 米.14. 计算: =.15. 有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为 .16. 如图,在矩形ABCD中,AB=1,∠DBC=30°.若将BD绕点B旋转后,点D落在BC延长线上的点E处,点D经过的路径为弧DE,则图中阴影部分的面积为.
 17. 如图,在梯形ABCD中,AD BC,AB⊥BC,AD=1,BC=3,点P是边AB上一点,如果把△BCP沿折痕CP向上翻折,点B恰好与点D重合,那么sin∠ADP为.
17. 如图,在梯形ABCD中,AD BC,AB⊥BC,AD=1,BC=3,点P是边AB上一点,如果把△BCP沿折痕CP向上翻折,点B恰好与点D重合,那么sin∠ADP为. 18. 今年8月20日,重庆八中学子在第37届全国青少年信息学奥林匹克竞赛中再创佳绩,斩获一金四银,一学子入选国家集训队,为了解我校信息竞赛同学对其它竞赛科目的兴趣程度,老师对同学们做了一次“我最喜爱的竞赛科目”问卷调查(每位同学都填了调查表,且只选择数学、物理、化学、生物其中一个科目),其中选物理的人数比选生物的少8人;选数学的人数是选生物人数的整数倍;选生物与数学的人数之和是物理与化学的人数之和的5倍;选化学与数学的人数之和比选物理与生物的人数之和多24人,则喜欢数学共有人.
18. 今年8月20日,重庆八中学子在第37届全国青少年信息学奥林匹克竞赛中再创佳绩,斩获一金四银,一学子入选国家集训队,为了解我校信息竞赛同学对其它竞赛科目的兴趣程度,老师对同学们做了一次“我最喜爱的竞赛科目”问卷调查(每位同学都填了调查表,且只选择数学、物理、化学、生物其中一个科目),其中选物理的人数比选生物的少8人;选数学的人数是选生物人数的整数倍;选生物与数学的人数之和是物理与化学的人数之和的5倍;选化学与数学的人数之和比选物理与生物的人数之和多24人,则喜欢数学共有人.三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 如图, ABC中,∠ACB=90°,∠B>∠A.
 (1)、用直尺和圆规在AC上确定一点D,∠BDC=2∠A,(不写作法,保留作图痕迹);(2)、若AB=10,BC=6,求CD长.21. 中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
(1)、用直尺和圆规在AC上确定一点D,∠BDC=2∠A,(不写作法,保留作图痕迹);(2)、若AB=10,BC=6,求CD长.21. 中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24<t≤48内的“声呐鲟”比去年多1尾,今年落在48<t≤72内的数据分别为49,60,68,68,71.去年20尾“声呐鲟”到达监测点A 所用时间t(h)的扇形统计图

今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图

关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数
中位数
众数
方差
去年
64.2
68
73
715.6
今年
56.2
a
68
629.7
(1)、请补全频数分布直方图,并根据以上信息填空:a=;(2)、中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;(3)、去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.22. 已知:如图,一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A. (1)、求点A的坐标.(2)、若一次函数y1与y2的图象与x轴分别相交于点B、C,求△ABC的面积.(3)、结合图象,直接写出y1≤y2时x的取值范围.23. 2020年是脱贫攻坚的关键年.为了让家乡早日实现脱贫目标,小伟利用网络平台帮助家乡销售特产“留香瓜”.已知小伟的家乡每年大约出产“留香瓜”600吨,利用网络平台进行销售前,人们主要依靠在本地自产自销和水果商贩上门收购,本地自产自销的价格为10元/千克,水果商贩上门收购的价格为8元/千克;利用网络平台进行销售后,因受网上销售火爆的影响,网上每销售100吨“留香瓜”,水果商贩的收购价将提高1元/千克.设网上销售价格为20元/千克,本地自产自销的价格仍然为10元/千克.(1)、利用网络平台进行销售前,小伟的家乡每年本地自产自销的总收入不超过卖给水果商贩收入的 ,求每年至少有多少吨“留香瓜”卖给了水果商贩?(2)、利用网络平台进行销售后,小伟的家乡每年销售“留香瓜”的总收入大约为920万元,其中本地自产自销“留香瓜”的销量按(1)问中的最大值计算,求每年在电商平台上销售了多少吨“留香瓜”?24. 对任意一个三位正整数n,如果n满足百位上的数字小于十位上的数字,且百位上的数字与十位上的数字之和等于个位上的数字,那么称这个数n为“攀登数”.用“攀登数”n的个位数字的平方减去十位数字的平方再减去百位数字的平方,得到的结果记为 .例如: ,满足 ,且 ,所以123是“攀登数”, ;例如: ,满足 ,但是 ,所以236不是“攀登数”;再如: ,满足 ,但是 ,所以314不是“攀登数”.(1)、判断369和147是不是“攀登数”,并说明理由;(2)、若t是“攀登数”,且t的3倍与t的个位数字的和能被7整除,求满足条件的“攀登数”t以及 的最大值.25. 已知抛物线y=﹣ x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.
(1)、求点A的坐标.(2)、若一次函数y1与y2的图象与x轴分别相交于点B、C,求△ABC的面积.(3)、结合图象,直接写出y1≤y2时x的取值范围.23. 2020年是脱贫攻坚的关键年.为了让家乡早日实现脱贫目标,小伟利用网络平台帮助家乡销售特产“留香瓜”.已知小伟的家乡每年大约出产“留香瓜”600吨,利用网络平台进行销售前,人们主要依靠在本地自产自销和水果商贩上门收购,本地自产自销的价格为10元/千克,水果商贩上门收购的价格为8元/千克;利用网络平台进行销售后,因受网上销售火爆的影响,网上每销售100吨“留香瓜”,水果商贩的收购价将提高1元/千克.设网上销售价格为20元/千克,本地自产自销的价格仍然为10元/千克.(1)、利用网络平台进行销售前,小伟的家乡每年本地自产自销的总收入不超过卖给水果商贩收入的 ,求每年至少有多少吨“留香瓜”卖给了水果商贩?(2)、利用网络平台进行销售后,小伟的家乡每年销售“留香瓜”的总收入大约为920万元,其中本地自产自销“留香瓜”的销量按(1)问中的最大值计算,求每年在电商平台上销售了多少吨“留香瓜”?24. 对任意一个三位正整数n,如果n满足百位上的数字小于十位上的数字,且百位上的数字与十位上的数字之和等于个位上的数字,那么称这个数n为“攀登数”.用“攀登数”n的个位数字的平方减去十位数字的平方再减去百位数字的平方,得到的结果记为 .例如: ,满足 ,且 ,所以123是“攀登数”, ;例如: ,满足 ,但是 ,所以236不是“攀登数”;再如: ,满足 ,但是 ,所以314不是“攀登数”.(1)、判断369和147是不是“攀登数”,并说明理由;(2)、若t是“攀登数”,且t的3倍与t的个位数字的和能被7整除,求满足条件的“攀登数”t以及 的最大值.25. 已知抛物线y=﹣ x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2. (1)、求抛物线的函数表达式和顶点B的坐标;(2)、如图1,抛物线与y轴交于点C,连接AC,过A作AD⊥x轴于点D,E是线段AC上的动点(点E不与A,C两点重合);
(1)、求抛物线的函数表达式和顶点B的坐标;(2)、如图1,抛物线与y轴交于点C,连接AC,过A作AD⊥x轴于点D,E是线段AC上的动点(点E不与A,C两点重合);(i)若直线BE将四边形ACOD分成面积比为1:3的两部分,求点E的坐标;
(ii)如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在y轴上的同时点F恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.
26. 如图,在平面直角坐标系中,▱ABOC的顶点A(0,2),点B(﹣4,0),点O为坐标原点,点C在第一象限,若将△AOB沿x轴向右运动得到△EFG(点A、O、B分别与点E、F、G对应),运动速度为每秒2个单位长度,边EF交OC于点P,边EG交OA于点Q,设运动时间为t(0<t<2)秒.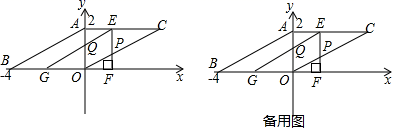 (1)、在运动过程中,线段AE的长度为(直接用含t的代数式表示);(2)、若t=1,求出四边形OPEQ的面积S;(3)、在运动过程中,是否存在四边形OPEQ为菱形?若存在,直接写出此时四边形OPEQ的面积;若不存在,请说明理由.
(1)、在运动过程中,线段AE的长度为(直接用含t的代数式表示);(2)、若t=1,求出四边形OPEQ的面积S;(3)、在运动过程中,是否存在四边形OPEQ为菱形?若存在,直接写出此时四边形OPEQ的面积;若不存在,请说明理由.