重庆市2021年初中学业水平模拟考试数学试卷三
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 的倒数的相反数( )A、2021 B、 C、-2021 D、2. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
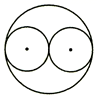 B、
B、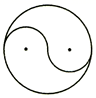 C、
C、 D、
D、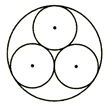 3. 下列调查中,最适宜采用普查方式的是( )A、对全国初中学生视力状况的调査 B、对“十一国庆”期间全国居民旅游出行方式的调查 C、旅客上飞机前的安全检查 D、了解某种品牌手机电池的使用寿命4. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则S四边形EFGH÷S四边形ABCD=( )
3. 下列调查中,最适宜采用普查方式的是( )A、对全国初中学生视力状况的调査 B、对“十一国庆”期间全国居民旅游出行方式的调查 C、旅客上飞机前的安全检查 D、了解某种品牌手机电池的使用寿命4. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则S四边形EFGH÷S四边形ABCD=( ) A、 B、 C、 D、5. 若关于x的一元二次方程(k﹣1)x2﹣2kx+k﹣3=0有实数根,则k的取值范围为( )A、k≥0 B、k≥0且k≠1 C、k≥ D、k≥ 且k≠16. 估计 的运算结果在哪两个整数之间?( )A、 和 B、 和 C、 和 D、 和7. 如图, 是 的直径, 为 的弦,且 于点 ,点 为圆上一点,若 , , ,则 的长为( )
A、 B、 C、 D、5. 若关于x的一元二次方程(k﹣1)x2﹣2kx+k﹣3=0有实数根,则k的取值范围为( )A、k≥0 B、k≥0且k≠1 C、k≥ D、k≥ 且k≠16. 估计 的运算结果在哪两个整数之间?( )A、 和 B、 和 C、 和 D、 和7. 如图, 是 的直径, 为 的弦,且 于点 ,点 为圆上一点,若 , , ,则 的长为( ) A、 B、 C、4 D、58. 如图,每一幅图中均含有若干个正方形,第1幅图中有1个正方形;第2幅图中有5个正方形……按这样的规律下去,第9幅图中正方形正的个数为( )
A、 B、 C、4 D、58. 如图,每一幅图中均含有若干个正方形,第1幅图中有1个正方形;第2幅图中有5个正方形……按这样的规律下去,第9幅图中正方形正的个数为( ) A、180 B、204 C、285 D、3859. 中国古代人民在生产生活中发现了许多数学问题,在《九章算术》中记载了这样一个问题,大意为:今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,则衡器两边的总重量相等,如果5只雀和6只燕的总重量为1斤,问雀、燕每1只各重多少斤?”如果设每只雀重x斤,每只燕重y斤,则下列方程组正确的是( )A、 B、 C、 D、10. 我校数学社团学生小明想测量学校对面斜坡 上的信号树 的高度,已知 的坡度为 ,且 的长度为65米,小明从坡底 处沿直线走到学校大台阶底部 处, 长为20米,他沿着与水平地面成30°夹角的大台阶行走20米到达平台 处,又向前走了13米到达平台上的旗杆 处,此时他仰望信号树的项部 ,测得仰角为50°,则信号树 的高度约为( )(小明的身高忽略不计)
A、180 B、204 C、285 D、3859. 中国古代人民在生产生活中发现了许多数学问题,在《九章算术》中记载了这样一个问题,大意为:今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,则衡器两边的总重量相等,如果5只雀和6只燕的总重量为1斤,问雀、燕每1只各重多少斤?”如果设每只雀重x斤,每只燕重y斤,则下列方程组正确的是( )A、 B、 C、 D、10. 我校数学社团学生小明想测量学校对面斜坡 上的信号树 的高度,已知 的坡度为 ,且 的长度为65米,小明从坡底 处沿直线走到学校大台阶底部 处, 长为20米,他沿着与水平地面成30°夹角的大台阶行走20米到达平台 处,又向前走了13米到达平台上的旗杆 处,此时他仰望信号树的项部 ,测得仰角为50°,则信号树 的高度约为( )(小明的身高忽略不计)(参考数据: , , , , )
 A、45米 B、30米 C、35米 D、40米11. 如图,在等腰 中, ,点 为反比例函数 (其中 )图象上的一点,点 在 轴正半轴上,过点 作 ,交反比例函数 的图象于点 ,连接 交 于点 ,若 的面积为2,则 的值为( )
A、45米 B、30米 C、35米 D、40米11. 如图,在等腰 中, ,点 为反比例函数 (其中 )图象上的一点,点 在 轴正半轴上,过点 作 ,交反比例函数 的图象于点 ,连接 交 于点 ,若 的面积为2,则 的值为( )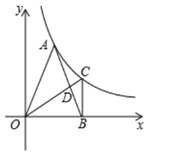 A、20 B、 C、16 D、12. 如果关于 的不等式组 无解,且关于 的分式方程 有正数解,则所有符合条件的整数 的值之和是( )A、3 B、4 C、7 D、8
A、20 B、 C、16 D、12. 如果关于 的不等式组 无解,且关于 的分式方程 有正数解,则所有符合条件的整数 的值之和是( )A、3 B、4 C、7 D、8二、填空题
-
13. 计算: .14. 根据世界卫生组织最新统计数据报道,截止到2020年12月2日全球累计“新冠肺炎”确诊病例已经超过63000000例,请将 63 000 000用科学记法表示为.15. 在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.小丽先从袋中随机摸出一个小球,再从袋中剩下的3个小球中随机摸出一个小球.小丽摸出的两个小球上的数字和为偶数的概率是.16. 如图,矩形 中, , , 是 中点,以点 为圆心, 为半径作弧交 于点 ,以点 为圆心, 为半径作弧交 于点 ,则图中阴影部分面积的差 为.
 17. 小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行.小宁先出发 5 分钟后,小强骑自行车匀速回家.小宁开始跑步中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35 分钟.两人之间的距离 y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示.则当弟弟到家时,小宁离图书馆的距离为米.
17. 小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行.小宁先出发 5 分钟后,小强骑自行车匀速回家.小宁开始跑步中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35 分钟.两人之间的距离 y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示.则当弟弟到家时,小宁离图书馆的距离为米. 18. 2019年4月底,37国元首携代表团在我国出席“一带一路”国际合作高峰论坛,为表友好,我国政府选择将刺绣与陶瓷两类工艺品作为国礼赠送给所有来宾.甲乙两个工厂分别承接了制作 , 两种刺绣 种陶瓷的任务.甲工厂安排100名工人制作刺绣,每人只能制作其中一种刺绣,乙工厂安排50名工人制作 种陶瓷, 的人均制作数量比 的人均制作数量少3件, 的人均制作量比 的人均制作量少20%,若本次赠送的国礼( , , 三样礼品)的人均制作数量比 的人均制作数量少30%,且 的人均制作数量为偶数件,则本次赠送的国礼共制作了件.
18. 2019年4月底,37国元首携代表团在我国出席“一带一路”国际合作高峰论坛,为表友好,我国政府选择将刺绣与陶瓷两类工艺品作为国礼赠送给所有来宾.甲乙两个工厂分别承接了制作 , 两种刺绣 种陶瓷的任务.甲工厂安排100名工人制作刺绣,每人只能制作其中一种刺绣,乙工厂安排50名工人制作 种陶瓷, 的人均制作数量比 的人均制作数量少3件, 的人均制作量比 的人均制作量少20%,若本次赠送的国礼( , , 三样礼品)的人均制作数量比 的人均制作数量少30%,且 的人均制作数量为偶数件,则本次赠送的国礼共制作了件.三、解答题
-
19. 计算(1)、 ;(2)、 .20. 已知:如图所示,在 中, 、 分别是 和 的角平分线,交 、 于点 、 ,连接 、 .
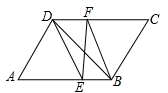 (1)、求证: 、 互相平分;(2)、若 , , ,求线段 的长.21. 函数图象在探索函数的性质中有非常重要的作用,现在就一类特殊的函数展开探索: ,探索函数图象和性质过程如下:
(1)、求证: 、 互相平分;(2)、若 , , ,求线段 的长.21. 函数图象在探索函数的性质中有非常重要的作用,现在就一类特殊的函数展开探索: ,探索函数图象和性质过程如下:…
-6
-4
-2
-1
-0.5
0.5
1
4
6
…
…
-4
-5
5
4
5
…
(1)、上表是该函数 与自变量 的几组对应值,则 . . ; (2)、如图,在平面直角坐标系中,已经描出了表中部分点,请根据描出的点画出该函数图象;(3)、由函数图象,写出该函数的一条性质:;(4)、请在同一个平面直角坐标系中画出函数 的图象,并直接写出不等式 的解集.22. 为了让师生更规范地操作教室里的一体机设备,学校信息技术处制作了“教室一体机设备培训”视频,并在读报课时间进行播放.结束后为了解初中校部(含小班)、新高中校部各班一体机管理员对设备操作知识的掌握程度,信息技术处对他们进行了相关的知识测试.现从初中、新高中各随机抽取了15名一体机管理员的成绩,得分用 表示,共分成4组: : , : , : , : ,对得分进行整理分析,给出了下面部分信息:
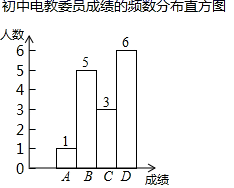
(2)、如图,在平面直角坐标系中,已经描出了表中部分点,请根据描出的点画出该函数图象;(3)、由函数图象,写出该函数的一条性质:;(4)、请在同一个平面直角坐标系中画出函数 的图象,并直接写出不等式 的解集.22. 为了让师生更规范地操作教室里的一体机设备,学校信息技术处制作了“教室一体机设备培训”视频,并在读报课时间进行播放.结束后为了解初中校部(含小班)、新高中校部各班一体机管理员对设备操作知识的掌握程度,信息技术处对他们进行了相关的知识测试.现从初中、新高中各随机抽取了15名一体机管理员的成绩,得分用 表示,共分成4组: : , : , : , : ,对得分进行整理分析,给出了下面部分信息:初中一体机管理员的测试成绩在 组中的数据为:81,85,88.
新高中一体机管理员的测试成绩:76,83,71,100,81,100,82,88,95,90,100,86,89,93,86.
成绩统计表如表:(注:极差为样本中最大数据与最小数据的差)
校部
平均数
中位数
最高分
众数
极差
初中
88
98
98
32
新高中
88
86
100
 (1)、 , , ;(2)、通过以上数据分析,你认为(填“初中”或“新高中”)的一体机管理员对一体机设备操作的知识掌握更好?请写出理由:;(3)、若初中、新高中共有240名一体机管理员,请估计此次测试成绩达到90分及以上的一体机管理员约有多少人?23. 一个正整数,若从左到右奇数位上的数字相同,偶数位上的数字相同,称这样的数为“接龙数”.例如:121,3535都是“接龙数”,123不是“接龙数”.(1)、求证:任意四位“接龙数”都能被101整除;(2)、若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数.对于任意的三位“接龙数” ,记F(t)= ﹣2 ﹣x,求使得F(t)为完全平方数的所有三位“接龙数” .24. 水果中的牛油果和桔子的维生素含量很高,因此深受人们喜爱,“农夫果园”水果商家11月份购进了第一批牛油果和桔子共300千克,已知牛油果进价每千克15元,售价每千克30元,桔子进价每千克5元,售价每千克10元.(1)、若这批牛油果和桔子全部销售完获利不低于3500元,则牛油果至少购进多少千克?(2)、第一批牛油果和桔子很快售完,于是商家决定购进第二批牛油果和桔子,牛油果和桔子的进价不变,牛油果售价比第一批上涨a%(其中a为正整数),桔子售价比第一批上涨2a%;销量与(1)中获得最低利润时的销量相比,牛油果的销量下降a%,桔子的销量保持不变,结果第二批中已经卖掉的牛油果和桔子的销售总额比(1)中第一批牛油果和桔子销售完后对应最低销售总额增加了2%,求正整数a的值.
(1)、 , , ;(2)、通过以上数据分析,你认为(填“初中”或“新高中”)的一体机管理员对一体机设备操作的知识掌握更好?请写出理由:;(3)、若初中、新高中共有240名一体机管理员,请估计此次测试成绩达到90分及以上的一体机管理员约有多少人?23. 一个正整数,若从左到右奇数位上的数字相同,偶数位上的数字相同,称这样的数为“接龙数”.例如:121,3535都是“接龙数”,123不是“接龙数”.(1)、求证:任意四位“接龙数”都能被101整除;(2)、若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数.对于任意的三位“接龙数” ,记F(t)= ﹣2 ﹣x,求使得F(t)为完全平方数的所有三位“接龙数” .24. 水果中的牛油果和桔子的维生素含量很高,因此深受人们喜爱,“农夫果园”水果商家11月份购进了第一批牛油果和桔子共300千克,已知牛油果进价每千克15元,售价每千克30元,桔子进价每千克5元,售价每千克10元.(1)、若这批牛油果和桔子全部销售完获利不低于3500元,则牛油果至少购进多少千克?(2)、第一批牛油果和桔子很快售完,于是商家决定购进第二批牛油果和桔子,牛油果和桔子的进价不变,牛油果售价比第一批上涨a%(其中a为正整数),桔子售价比第一批上涨2a%;销量与(1)中获得最低利润时的销量相比,牛油果的销量下降a%,桔子的销量保持不变,结果第二批中已经卖掉的牛油果和桔子的销售总额比(1)中第一批牛油果和桔子销售完后对应最低销售总额增加了2%,求正整数a的值.