浙江省温州市鹿城区2021年初中毕业升学考试数学模拟试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 3的相反数是( )A、 3 B、-3 C、 D、2. 截止2021年3月21日,电影《你好,李焕英》的票房已突破5310000000元,其中数据5310000000用科学记数法表示为( )A、 B、 C、 D、3. 如图所示,某物体由4块立方体组成,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 一只不透明的盒子里装有9个只有颜色不同的球,其中红球4个、白球3个、黑球2个.从盒子里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、5. 某校举办了一次“交通安全知识”测试,王老师从全校学生的答卷中随机地抽取了200名学生的答卷,并将测试成绩分为 , , , 四个等级,绘制成如图所示的条形统计图.若该校学生共有1000人,则该校成绩为 的学生人数估计为( )
4. 一只不透明的盒子里装有9个只有颜色不同的球,其中红球4个、白球3个、黑球2个.从盒子里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、5. 某校举办了一次“交通安全知识”测试,王老师从全校学生的答卷中随机地抽取了200名学生的答卷,并将测试成绩分为 , , , 四个等级,绘制成如图所示的条形统计图.若该校学生共有1000人,则该校成绩为 的学生人数估计为( ) A、30 B、75 C、150 D、2006. 如图,小华在课外时间利用仪器测量红旗的高度,从点 处测得旗杆顶部 的仰角为 ,并测得到旗杆的距离 为 米,若 为 米,则红旗的高度 为( )
A、30 B、75 C、150 D、2006. 如图,小华在课外时间利用仪器测量红旗的高度,从点 处测得旗杆顶部 的仰角为 ,并测得到旗杆的距离 为 米,若 为 米,则红旗的高度 为( ) A、 米 B、 米 C、 米 D、 米7. 一家工艺品厂按计件方式结算工资.小鹿去这家工艺品厂打工,第一天工资60元,第二天比第一天多做了5件,工资为75元.设小鹿第一天做了 件,根据题意可列出方程为( )A、 B、 C、 D、8. 《几何原本》里有一个图形:在 中, , 是边 上的两点 ,且满足 ,过点 , 分别作 的平行线,过点 作 的平行线,它们将 分成加图的5个部分,其面积依次记为 , , , , , , ,则 的值为( )
A、 米 B、 米 C、 米 D、 米7. 一家工艺品厂按计件方式结算工资.小鹿去这家工艺品厂打工,第一天工资60元,第二天比第一天多做了5件,工资为75元.设小鹿第一天做了 件,根据题意可列出方程为( )A、 B、 C、 D、8. 《几何原本》里有一个图形:在 中, , 是边 上的两点 ,且满足 ,过点 , 分别作 的平行线,过点 作 的平行线,它们将 分成加图的5个部分,其面积依次记为 , , , , , , ,则 的值为( ) A、9 B、18 C、27 D、549. 在平面直角坐标系中,点 , 的坐标分别为 , ,若抛物线 与线段 有且只有一个交点,则 的值可以是( )A、 B、 C、1 D、10. 如图, , 分别是正方形 边 , 上的点, .以 , 为边作 ,连结 并延长交 于点 ,连结 .若 ,则 的长为( )
A、9 B、18 C、27 D、549. 在平面直角坐标系中,点 , 的坐标分别为 , ,若抛物线 与线段 有且只有一个交点,则 的值可以是( )A、 B、 C、1 D、10. 如图, , 分别是正方形 边 , 上的点, .以 , 为边作 ,连结 并延长交 于点 ,连结 .若 ,则 的长为( )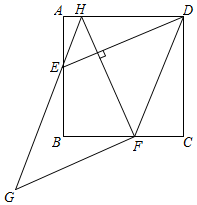 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: = .12. 不等式2x﹣1>3的解集为13. 已知圆的半径为2cm,90°圆心角所对的弧长为cm.14. 如图,点 在反比例函数 的图象上,则 的面积为.
 15. 如图,直线 分别与 轴, 轴交于点 , ,直线 分别与 轴, 轴交于点 , ,直线 , 相交于点 ,将 向右平移5个单位得到 ,若点 好落在直线 上,则 .
15. 如图,直线 分别与 轴, 轴交于点 , ,直线 分别与 轴, 轴交于点 , ,直线 , 相交于点 ,将 向右平移5个单位得到 ,若点 好落在直线 上,则 . 16. 某厂家设计一种双层长方体垃圾桶, cm, cm, cm,侧面如图1所示, 为隔板,等分上下两层.下方内桶 绕底部轴 旋转打开,若点 恰好能卡在原来点 的位置,则内桶边 的长度应设计为cm;现将 调整为25cm,打开最大角度时,点 卡在隔板上,如图2所示,可完全放入下方内桶的球体的直径不大于cm.
16. 某厂家设计一种双层长方体垃圾桶, cm, cm, cm,侧面如图1所示, 为隔板,等分上下两层.下方内桶 绕底部轴 旋转打开,若点 恰好能卡在原来点 的位置,则内桶边 的长度应设计为cm;现将 调整为25cm,打开最大角度时,点 卡在隔板上,如图2所示,可完全放入下方内桶的球体的直径不大于cm.
三、解答题
-
17. 计算:(1)、 .(2)、化简: .18. 如图,在 中, ,点 , 在 上 , .
 (1)、求证: ≌ .(2)、若 , ,求 的长.19. 某学校在一次广播操比赛中,901班,902班,903班的各项得分如表:
(1)、求证: ≌ .(2)、若 , ,求 的长.19. 某学校在一次广播操比赛中,901班,902班,903班的各项得分如表:班级
服装统一
动作整齐
动作准确
901班
85
70
85
902班
75
85
80
903班
90
85
95
(1)、若取三个项目的得分平均分作为该班成绩,分别求各班的成绩.(2)、若学校认为三个项目的重要程度各不相同,从低到高依次为“服装统一”“动作整齐”“动作准确”,它们在总分中所占的比例分别为10%, %, %.请你设计一组符合要求的 , 值,并直接给出三个班级的排名顺序.20. 如图,将一个长为8,宽为6的大矩形分割成如图所示24个全等的小长方形,它们的顶点称为格点.请按下列要求分别作出格点三角形和格点四边形.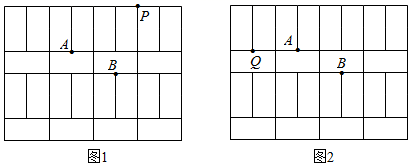
( 1 )在图1中画出一个等腰 ,使点 , 在 内部(不包括在 边上).
( 2 )在图2中画出一个矩形 ,使点 , 在矩形 内部(不包括在矩形 边上)
21. 如图,抛物线 交 轴于 , 两点,点 在点 左侧,点 的坐标为 , ,过点 作 轴交抛物线于点 ,过点 作 交抛物线于点 .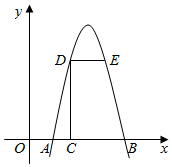 (1)、若点 的坐标为 ,求 的长.(2)、当 时,求 的值.22. 如图, 是 的直径,点 为圆上一点,点 为 的中点,连结 ,作 交 的延长线于点 .
(1)、若点 的坐标为 ,求 的长.(2)、当 时,求 的值.22. 如图, 是 的直径,点 为圆上一点,点 为 的中点,连结 ,作 交 的延长线于点 .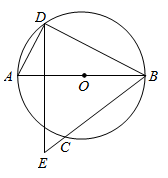 (1)、求证: .(2)、连结 并延长交 于点 ,若 , ,求 的半径.23. 下表是某奶茶店的一款奶茶近两天的销售情况.
(1)、求证: .(2)、连结 并延长交 于点 ,若 , ,求 的半径.23. 下表是某奶茶店的一款奶茶近两天的销售情况.销售情况
销售数量(单位:杯)
销售收入(单位:元)
小杯
大杯
第一天
20
30
460
第二天
25
25
450
(1)、问这款奶茶小杯和大杯的销售单价各是多少元?(2)、已知这款奶茶小杯成本4元/杯,大杯成本5元/杯,奶茶店每天只能供应80杯该款奶茶,其中小杯不少于10杯,求该款奶茶一天的最大利润.(销售利润=销售收入-成本)(3)、为了满足市场的需求,奶茶店推出每杯2元的加料服务,顾客在选完杯型后可以自主选择加料或者不加料.小明恰好用了208元购买该款奶茶,其中小杯不加料的数量是总杯数的 ,则小明这款奶茶大杯加料的买了杯.24. 如图,在矩形 中, , ,过对角线 上一点 作 的垂线交 于点 ,交 于点 ,过点 作 交 于点 ,连结 交 于点 ,连结 . (1)、求 的值.(2)、当四边形 有一组邻边相等时,求 的长.(3)、点 关于 的对称点记为 ,若 落在 内部(不包含边界),求 长度的取值范围.
(1)、求 的值.(2)、当四边形 有一组邻边相等时,求 的长.(3)、点 关于 的对称点记为 ,若 落在 内部(不包含边界),求 长度的取值范围.