浙江省绍兴市柯桥区2021年初中学业水平适应性考试数学试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 下列四个数中,最小的是( )A、﹣(﹣4) B、|﹣1| C、0 D、﹣32. 三本相同的书本叠成如图所示的几何体,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,已知不透明的袋中装有红色、黄色、蓝色的乒乓球共120个,某学习小组做“用频率估计概率”的摸球实验(从中随机摸出一个球,记下颜色后放回),统计了“摸出球为红色”出现的频率,绘制了如图折线统计图,那么估计袋中红色球的数目为( )
3. 如图,已知不透明的袋中装有红色、黄色、蓝色的乒乓球共120个,某学习小组做“用频率估计概率”的摸球实验(从中随机摸出一个球,记下颜色后放回),统计了“摸出球为红色”出现的频率,绘制了如图折线统计图,那么估计袋中红色球的数目为( )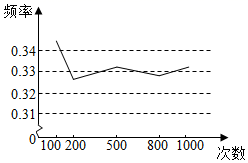 A、20 B、30 C、40 D、604. 如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
A、20 B、30 C、40 D、604. 如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )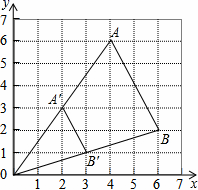 A、 B、(m,n) C、 D、5. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )
A、 B、(m,n) C、 D、5. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )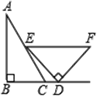 A、 B、 C、 D、6. 如图, 中, ,它的周长为16,若圆O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A、 B、 C、 D、6. 如图, 中, ,它的周长为16,若圆O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )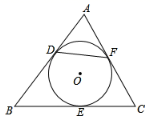 A、2 B、3 C、4 D、67. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算2( ﹣1)的值( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间8. 如图,已知 , 为 上一点,以 为半径的圆经过点 ,且与 、 交于点 、 ,设 , ,则( )
A、2 B、3 C、4 D、67. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算2( ﹣1)的值( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间8. 如图,已知 , 为 上一点,以 为半径的圆经过点 ,且与 、 交于点 、 ,设 , ,则( )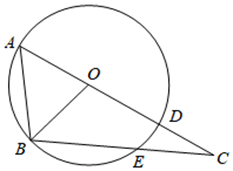 A、若 ,则弧 的度数为 B、若 ,则弧 的度数为 C、若 ,则弧 的度数为 D、若 ,则弧 的度数为9. 利用函数知识对关于代数式 的以下说法作出判断,则正确的有( )
A、若 ,则弧 的度数为 B、若 ,则弧 的度数为 C、若 ,则弧 的度数为 D、若 ,则弧 的度数为9. 利用函数知识对关于代数式 的以下说法作出判断,则正确的有( )①如果存在两个实数 ,使得 ,则 ②存在三个实数 ,使得 ③如果 ,则一定存在两个实数 ,使 ④如果 ,则一定存在两个实数 ,使
A、1个 B、2个 C、3个 D、4个10. 如图,现有3×3的方格,每个小方格内均有数字,要求方格内每一行.每一列以及每一条对角线上的三个数字之和均相等,记三个数字之和为P,则P的值是( )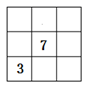 A、12 B、15 C、18 D、21
A、12 B、15 C、18 D、21二、填空题
-
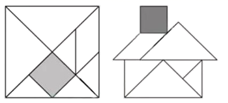
11. 分解因式:x3-x= .12. “七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”,图①是由边长 的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为 (结果保留根号).
 13. 学校组织七年级500名学生搬桌椅,规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为14. 如图直角坐标系中,矩形ABCD的边AB在x轴上,反比例函数 第一象限内的图象经过点C,坐标原点O在AB边上,E在AD边上,AD=4DE,BE交y轴于点F,若△ABF的面积为12,则 的值是.
13. 学校组织七年级500名学生搬桌椅,规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为14. 如图直角坐标系中,矩形ABCD的边AB在x轴上,反比例函数 第一象限内的图象经过点C,坐标原点O在AB边上,E在AD边上,AD=4DE,BE交y轴于点F,若△ABF的面积为12,则 的值是.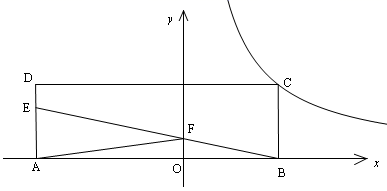 15. 等腰三角形ABC中,过C作CD⊥AB交AB边于点E,且AB=AC=CD,连结AD并延长交CB延长线于点F,若DB=5.BC=8,则∠AFC= , AB=.
15. 等腰三角形ABC中,过C作CD⊥AB交AB边于点E,且AB=AC=CD,连结AD并延长交CB延长线于点F,若DB=5.BC=8,则∠AFC= , AB=.三、解答题
-
16. 计算:(1)、(2)、17. 为了解学生对校园网站五个栏目的喜爱情况(规定每名学生只能选一个最喜爱的).学校随机抽取了部分学生进行调查,将调查结果整理后绘制成如下两幅不完整的统计图,请结合图中提供的信息解答下列问题:
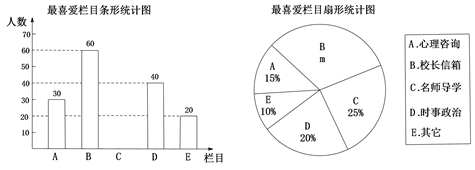 (1)、本次被调查的学生有人,扇形统计图中m =;(2)、将条形统计图补充完整;(3)、若该校有1800名学生,估计全校最喜爱“校长信箱”栏目的学生有多少人?18. 如图,在圆O中,过半径OD的中点C作 交圆O于A、B两点,且 .
(1)、本次被调查的学生有人,扇形统计图中m =;(2)、将条形统计图补充完整;(3)、若该校有1800名学生,估计全校最喜爱“校长信箱”栏目的学生有多少人?18. 如图,在圆O中,过半径OD的中点C作 交圆O于A、B两点,且 .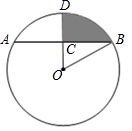 (1)、求OD的长;(2)、计算阴影部分的周长.19. 如图,已知二次函数 的图象经过 , 两点.
(1)、求OD的长;(2)、计算阴影部分的周长.19. 如图,已知二次函数 的图象经过 , 两点. (1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.20. 如图2,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,展开小桌板使桌面保持水平时如图1,小桌板的边沿O点与收起时桌面顶端A点的距离OA=75厘米,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与支架长BC的长度之和等于OA的长度.
(1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.20. 如图2,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,展开小桌板使桌面保持水平时如图1,小桌板的边沿O点与收起时桌面顶端A点的距离OA=75厘米,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与支架长BC的长度之和等于OA的长度.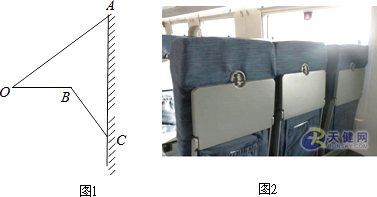 (1)、求∠CBO的度数;(2)、求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)21.
(1)、求∠CBO的度数;(2)、求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)21.
如图1,在 中, ,点D为 边上的动点, 交 于点E.
(1)、问题发现:如图2,当 时, ; 与 所在直线相交所成的锐角等于.(2)、类比探究:当 时,把 绕点A逆时针旋转到如图3的位置时,请求出 的值以及 与 所在直线相交所成的锐角.22. 某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.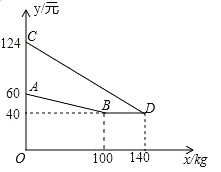 (1)、请解释图中点D的实际意义.(2)、求线段CD所表示的y2与x之间的函数表达式.(3)、当该产品产量为多少时,获得的利润最大?最大利润是多少?23. 如图,E是正方形ABCD边BC上一点,连结AE,分别过B,D作BG⊥AE,DF⊥AE,垂足为G,F,∠DFE的平分线交CD于点H,交对角线AC于点O,
(1)、请解释图中点D的实际意义.(2)、求线段CD所表示的y2与x之间的函数表达式.(3)、当该产品产量为多少时,获得的利润最大?最大利润是多少?23. 如图,E是正方形ABCD边BC上一点,连结AE,分别过B,D作BG⊥AE,DF⊥AE,垂足为G,F,∠DFE的平分线交CD于点H,交对角线AC于点O,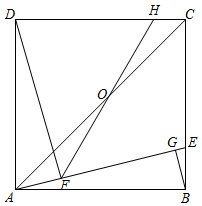 (1)、直接写出DF,FG,GB三条线段的数量关系;(2)、求证:AO=CO;(3)、若BG=1,DF=5,求OH的长度.
(1)、直接写出DF,FG,GB三条线段的数量关系;(2)、求证:AO=CO;(3)、若BG=1,DF=5,求OH的长度.