浙江省金衢十二校2021年数学中考模拟联考试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 2021 B、﹣2021 C、 D、±20212. 在下面由冬季奥运会比赛项目图标组成的四个图形中,其中可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算,正确的是( )A、4a﹣2a=2 B、a6÷a3=a2 C、(a﹣b) 2=a2﹣b2 D、(﹣a3b) 2=a6b24. 新型冠状病毒(2019-nCoV)的直径约为0.00000012米.用科学记数法可将0.00000012表示为( )A、1.2×10-6 B、1.2×10-7 C、12×10-8 D、12×10-75. 为调查某班学生每天使用零花钱的情况,小明随机调查了30名同学,结果如表:
3. 下列运算,正确的是( )A、4a﹣2a=2 B、a6÷a3=a2 C、(a﹣b) 2=a2﹣b2 D、(﹣a3b) 2=a6b24. 新型冠状病毒(2019-nCoV)的直径约为0.00000012米.用科学记数法可将0.00000012表示为( )A、1.2×10-6 B、1.2×10-7 C、12×10-8 D、12×10-75. 为调查某班学生每天使用零花钱的情况,小明随机调查了30名同学,结果如表:每天使用零花钱(单位:元)
5
10
15
20
25
人数
2
5
8
9
6
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A、9,6 B、20,25 C、20,17.5 D、9,256. 已知二次函数 的部分图象如图所示,则使得函数值 大于 的自变量 的取值可以是( ) A、-4 B、-2 C、0 D、27. 已知关于x的方程 无解,则m的值为( )A、4 B、3 C、2 D、18. 如图,把一个长方形纸片对折两次,然后沿图中虚线剪下一个角,若打开后得到一个正方形纸片,剪切线与折痕所成的角的大小等于( )
A、-4 B、-2 C、0 D、27. 已知关于x的方程 无解,则m的值为( )A、4 B、3 C、2 D、18. 如图,把一个长方形纸片对折两次,然后沿图中虚线剪下一个角,若打开后得到一个正方形纸片,剪切线与折痕所成的角的大小等于( ) A、90° B、60° C、45° D、30°9. 下列选项中,能够被半径为1的圆及其内部所覆盖的图形是( )A、长度为 的线段 B、斜边为3的直角三角形 C、面积为4的菱形 D、半径为 ,圆心角为 的扇形10. 如图,在矩形ABCD中, , , 一个三角形的直角顶点E是边AB上的一动点,一直角边过点D , 另一直角边与BC交于F , 若 , , 则y关于x的函数关系的图象大致为( )
A、90° B、60° C、45° D、30°9. 下列选项中,能够被半径为1的圆及其内部所覆盖的图形是( )A、长度为 的线段 B、斜边为3的直角三角形 C、面积为4的菱形 D、半径为 ,圆心角为 的扇形10. 如图,在矩形ABCD中, , , 一个三角形的直角顶点E是边AB上的一动点,一直角边过点D , 另一直角边与BC交于F , 若 , , 则y关于x的函数关系的图象大致为( ) A、
A、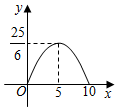 B、
B、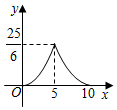 C、
C、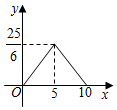 D、
D、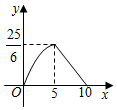
二、填空题
-
11. 因式分解:x2-4y2= .12. 木工师傅用刨子可将木板刨平,如图,经过刨平的木板上的两个点,而且只能弹出一条墨线,其数学原理为.
 13. 如图,在游园活动中,数学小组制作了一面“赵爽弦图”,AC=50cm,AB=30cm,他击中阴影部分的概率是.
13. 如图,在游园活动中,数学小组制作了一面“赵爽弦图”,AC=50cm,AB=30cm,他击中阴影部分的概率是. 14. 如图,放置在直线l上的扇形OAB,由图①滚动(无滑动)到图②,再由图②滚动到图③,若半径OA=1,∠AOB=90°,则点O所经过的路径长是.
14. 如图,放置在直线l上的扇形OAB,由图①滚动(无滑动)到图②,再由图②滚动到图③,若半径OA=1,∠AOB=90°,则点O所经过的路径长是. 15. 如图,在△AOB中,OC平分∠AOB, = ,反比例函数 (k<0)图象经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为.
15. 如图,在△AOB中,OC平分∠AOB, = ,反比例函数 (k<0)图象经过点A、C两点,点B在x轴上,若△AOB的面积为7,则k的值为. 16. 图1是上下都安装“摩擦铰链”的平开窗,滑轨MN固定在窗框,托悬臂CF安装在窗上.A,D,E分别是MN,CF,AD上固定的点,且BC=DE.当窗户开到最大时,CF⊥MN,且点C到MN的距离为8cm,此时主轴AD与MN的夹角∠DAN=45°.如图2,窗户从开到最大到关闭(CF,AD,BC,BE与MN重合)的过程中,控制臂BC,带动MN上的滑块B向点N滑动了30cm.则
16. 图1是上下都安装“摩擦铰链”的平开窗,滑轨MN固定在窗框,托悬臂CF安装在窗上.A,D,E分别是MN,CF,AD上固定的点,且BC=DE.当窗户开到最大时,CF⊥MN,且点C到MN的距离为8cm,此时主轴AD与MN的夹角∠DAN=45°.如图2,窗户从开到最大到关闭(CF,AD,BC,BE与MN重合)的过程中,控制臂BC,带动MN上的滑块B向点N滑动了30cm.则 (1)、BE和CD的数量关系是;(2)、AD的长为cm.
(1)、BE和CD的数量关系是;(2)、AD的长为cm.三、解答题
-
17. 计算:2﹣1+4cos30°﹣ ﹣|﹣ |.18. 解不等式组: .19. 如图是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.点A,B均在格点上
 (1)、在图1中画出AB的中点O;(保留辅助线,辅助线用虚线)(2)、在图2中画一个Rt△ABC,使点C在格点上.(不写作法,保留作图痕迹)20. 某校为了解本校学生每周参加课外辅导班的情况,随机调查了部分学生一周内参加课外辅导班的学科数,并将调查结果绘制成如图1、图2所示的两幅不完整统计图(其中A:0个学科,B:1个学科,C:2个学科,D:3个学科,E:4个学科或以上),解答下列问题:
(1)、在图1中画出AB的中点O;(保留辅助线,辅助线用虚线)(2)、在图2中画一个Rt△ABC,使点C在格点上.(不写作法,保留作图痕迹)20. 某校为了解本校学生每周参加课外辅导班的情况,随机调查了部分学生一周内参加课外辅导班的学科数,并将调查结果绘制成如图1、图2所示的两幅不完整统计图(其中A:0个学科,B:1个学科,C:2个学科,D:3个学科,E:4个学科或以上),解答下列问题: (1)、请计算B组的人数,并将图2中的统计图补充完整;(2)、若该校共有2000名学生,根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科(含3个学科)以上的学生共有多少人?21. 图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.
(1)、请计算B组的人数,并将图2中的统计图补充完整;(2)、若该校共有2000名学生,根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科(含3个学科)以上的学生共有多少人?21. 图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴. (1)、当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.(2)、如果小华要洗脚,需要调整水柱AE,使点E与点D重合
(1)、当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.(2)、如果小华要洗脚,需要调整水柱AE,使点E与点D重合①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.(参考数据: ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
22. 如图,在△ABC中,∠ACB=90°,以OA为半径的⊙O与BC相切于点D,与AB交于点E (1)、求证:AE=AF;(2)、若DE=3,sin∠BDE= ,求AC的长.23. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b= ﹣2.某班“数学兴趣小组”对此函数进一步推广 ﹣2,现对这个函数的图象和性质进行了探究,请补充完整:
(1)、求证:AE=AF;(2)、若DE=3,sin∠BDE= ,求AC的长.23. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b= ﹣2.某班“数学兴趣小组”对此函数进一步推广 ﹣2,现对这个函数的图象和性质进行了探究,请补充完整: (1)、类比反比例函数可知,函数y= ﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是.(2)、“数学兴趣小组”进一步思考函数y=| ﹣2|的图象和性质,请根据函数y= -2的图象,画出函数y=| ﹣2|的图象;(3)、结合函数y=| ﹣2|的图象解答下列问题:
(1)、类比反比例函数可知,函数y= ﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是.(2)、“数学兴趣小组”进一步思考函数y=| ﹣2|的图象和性质,请根据函数y= -2的图象,画出函数y=| ﹣2|的图象;(3)、结合函数y=| ﹣2|的图象解答下列问题:①求出方程| ﹣2|=0的根;
②如果方程| ﹣2|=a有2个实数根,请直接写出a的取值范围.
24. 如图,在△ABC中,AB=5,AC=9,S△ABC= ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,点Q以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH. (1)、求tanA的值;(2)、设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,若不存在,请说明理由;(3)、当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上
(1)、求tanA的值;(2)、设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,若不存在,请说明理由;(3)、当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上