浙江省杭州市江干区2021年数学中考二模试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 若a的相反数是2,则a的值为( )A、2 B、﹣2 C、﹣ D、±22. 截止2020年8月31日,为期62天(7月1日至8月31日)的铁路暑运圆满收官,杭州火车东站累计发送旅客973.41万人次,发送量位列长三角铁路客站首位.数据973.41万可用科学记数法表示为( )A、 B、 C、 D、3. 如图, , 交 与 , ,则 的度数是( )
 A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 如图,已知 , ,用尺规作图的方法在 上取一点 ,使得 ,则下列选项正确的是( )A、
A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 如图,已知 , ,用尺规作图的方法在 上取一点 ,使得 ,则下列选项正确的是( )A、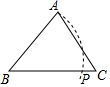 B、
B、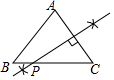 C、
C、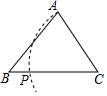 D、
D、 6. 如图反映了我国2014-2019年快递业务量(位:亿件)及年增长率(%)的情况
6. 如图反映了我国2014-2019年快递业务量(位:亿件)及年增长率(%)的情况

(以上数据来源于国家统计局网站)
根据统计图提供的信息,下列推断不合理的是( )
A、2014-2019年,我国快递业务量的年平均值超过300亿件 B、与2017年相比,2018年我国快递业务量的增长率超过25% C、2014-2019年,我国快递业务量与年增长率都是逐年增长 D、2019年我国的快递业务量比2014年的4倍还多7. 如图,一次函数 和正比例函数 在同一坐标系内的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 随着快递业务量的增加,某快递公司为快递品更换快捷的交通工具,公司投递快件的能力由每天300件提高到420件,平均每人每天比原来多投递8件.若快递公司的快递员人数不变,求原来平均每人每天投递快件多少件?设原来平均每人每天投递快件 件,根据题意可列方程为( )A、 B、 C、 D、9. 已知 ,且 ,其中 , ,则 的取值范围( )A、 B、 C、 D、10. 如图,在正方形 中,对角线 , 相交于点 ,点 在 边上,且 ,连接 交 于点 ,过点 作 ,连接 并延长,交 于点 ,过点 作 分别交 , 于点 , ,交 的延长线于点 ,现给出下列结论:① ;② ;③ ;④ .其中正确的结论有( )
8. 随着快递业务量的增加,某快递公司为快递品更换快捷的交通工具,公司投递快件的能力由每天300件提高到420件,平均每人每天比原来多投递8件.若快递公司的快递员人数不变,求原来平均每人每天投递快件多少件?设原来平均每人每天投递快件 件,根据题意可列方程为( )A、 B、 C、 D、9. 已知 ,且 ,其中 , ,则 的取值范围( )A、 B、 C、 D、10. 如图,在正方形 中,对角线 , 相交于点 ,点 在 边上,且 ,连接 交 于点 ,过点 作 ,连接 并延长,交 于点 ,过点 作 分别交 , 于点 , ,交 的延长线于点 ,现给出下列结论:① ;② ;③ ;④ .其中正确的结论有( ) A、①③ B、②④ C、①②③ D、①②③④
A、①③ B、②④ C、①②③ D、①②③④二、填空题
-
11. 计算: .(请写出中间步骤)12. 关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是.13. 小红的口袋有3把钥匙,分别能打开甲、乙、丙三把锁,他从口袋中任意取出一把钥匙,能打开甲锁的概率是.14. 如图,折叠矩形纸片 ,先把 沿 翻折,点 落在 边上的点 处,折痕为 ,点 在 上;然后将纸片展开铺平,把矩形 沿对角线 折叠,若点 恰好落在对角线 上,则 的值为.
 15. 一次函数 和 相交于 , 两点,则不等式 的解集为.16. 如图, 的弦 、 相交于点 , 为弧 的中点,过点 作 的切线交 的延长线于点 ,连接 ,若 , 的半径为 , ,则 .
15. 一次函数 和 相交于 , 两点,则不等式 的解集为.16. 如图, 的弦 、 相交于点 , 为弧 的中点,过点 作 的切线交 的延长线于点 ,连接 ,若 , 的半径为 , ,则 .
三、解答题
-
17.(1)、化简: ;(2)、计算:18. 某校为了解学生每天在校体育活动的时间(单位: ),随机调查了该校的部分学生,根据调查结果绘制出如图所示的统计图.
 (1)、求被调查的学生人数为 , ;(2)、求被调查的学生每天在校体育活动时间的平均数、众数;(3)、若该校有1500名学生,估计该校每天在校体育活动时间大于 的学生人数.19. 如图,在 中, , , , , , ,求:
(1)、求被调查的学生人数为 , ;(2)、求被调查的学生每天在校体育活动时间的平均数、众数;(3)、若该校有1500名学生,估计该校每天在校体育活动时间大于 的学生人数.19. 如图,在 中, , , , , , ,求: (1)、 与 的度数;(2)、 的长.20. 一辆小型客车从甲地出发前往乙地,如以 的平均速度则 到达目的地.(1)、当小型客车从乙地返回时,它的平均速度 与时间 有怎样的函数关系?(2)、小型客车上午8时从乙地出发.
(1)、 与 的度数;(2)、 的长.20. 一辆小型客车从甲地出发前往乙地,如以 的平均速度则 到达目的地.(1)、当小型客车从乙地返回时,它的平均速度 与时间 有怎样的函数关系?(2)、小型客车上午8时从乙地出发.①小型客车需在当天14点15分至15点30分间(含14点15分与15点30分)返回甲地,求其行驶平均速度 的取值范围;
②如小型客车的最高限速是 ,该小型客车能否在当天12点30分前返回甲地?请说明理由.

