西藏日喀则市2021年数学中考二模试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. -4的绝对值是( )A、-4 B、 C、4 D、2. 下列运算正确的是( )A、4a-a=3 B、2(2a-b)=4a-b C、(a+b)2=a2+b2 D、(a+2)(a-2)=a2-43. 2021年3月5日,国务院总理李克强作政府工作报告,报告称2020年全国新增城镇就业人口1186万人,将1186万用科学记数法可表示为( )A、 1.186×108 B、1.186×107 C、1.186×106 D、1.186×1054. 如图,下列汽车标志中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )
5. 如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )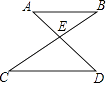 A、35° B、45° C、70° D、80°6. 如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )
A、35° B、45° C、70° D、80°6. 如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )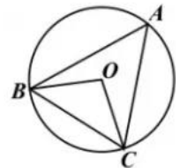 A、50° B、55° C、60° D、65°7. 一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别( )A、4,4 B、3,4 C、4,3 D、3,38. 不等式组 的解集在数轴上表示正确的是( )A、
A、50° B、55° C、60° D、65°7. 一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的平均数、中位数分别( )A、4,4 B、3,4 C、4,3 D、3,38. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 9. 将抛物线y=2x2向左平移2个单位,再向下平移5个单位得到的抛物线是( )A、y=2(x-2)2-5 B、y=2(x+2)2-3 C、y=2(x+2)2+3 D、y=2(x+2)2-510. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
9. 将抛物线y=2x2向左平移2个单位,再向下平移5个单位得到的抛物线是( )A、y=2(x-2)2-5 B、y=2(x+2)2-3 C、y=2(x+2)2+3 D、y=2(x+2)2-510. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )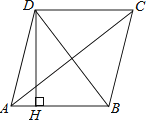 A、 B、 C、12 D、2411. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )
A、 B、 C、12 D、2411. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )
A、 B、
B、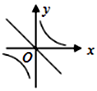 C、
C、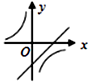 D、
D、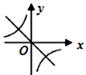 12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4ac﹣b2>0;④2a+b=0
其中正确的结论有( )
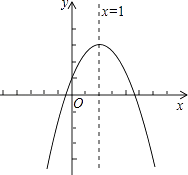 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
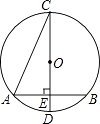
13. 当 时,分式 值为零.14. 因式分解: .15. 已知 且 = ,则 为16. 如果点A(﹣2,y1),B(﹣1,y2),都在反比例函数y= (k>0)的图象上,那么y1 , y2 的大小关系是(请用“<”表示出来)17. 如图,已知⊙O的直径CD垂直于弦AB,∠ACD=22.5°,若CD=6cm,则AB的长为 cm.
 18.
18.如图是由火柴棒搭成的几何图案,则第n个图案中有 根火柴棒.(用含n的代数式表示)

三、解答题
-
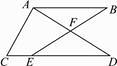
19. 计算:( ﹣2)0+( )﹣1﹣2cos30°﹣| ﹣2|20. 先化简,再求值: ,其中x=2.21. 如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.
 22. 今年新冠肺炎疫情在全球肆虐,为降低病亡率,某工厂平均每天比原计划多生产10台呼吸机,现在生产120台呼吸机的时间与原计划生产90台呼吸机所需时间相同.求该工厂原来平均每天生产多少台呼吸机?23. 为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整)
22. 今年新冠肺炎疫情在全球肆虐,为降低病亡率,某工厂平均每天比原计划多生产10台呼吸机,现在生产120台呼吸机的时间与原计划生产90台呼吸机所需时间相同.求该工厂原来平均每天生产多少台呼吸机?23. 为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整)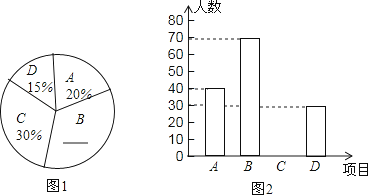 (1)、这次调查中,一共调查了 名学生。
(1)、这次调查中,一共调查了 名学生。
(2)、请补全两幅统计图。
(3)、若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率。
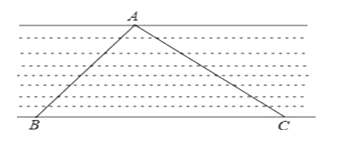
24. 陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学的路程与所用时间的关系示意图.根据图中提供的信息回答下列问题: (1)、陈杰家到学校的距离是多少米?书店到学校的距离是多少米?(2)、陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?(3)、在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?(4)、如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?25. 如图,为了求某条河的宽度,在它的对岸岸边任意取一点A,再在河的这边沿河边取两点B、C,使得∠ABC=45°,∠ACB=30°,量得BC的长为40m,求河的宽度(结果保留根号).
(1)、陈杰家到学校的距离是多少米?书店到学校的距离是多少米?(2)、陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?(3)、在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?(4)、如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?25. 如图,为了求某条河的宽度,在它的对岸岸边任意取一点A,再在河的这边沿河边取两点B、C,使得∠ABC=45°,∠ACB=30°,量得BC的长为40m,求河的宽度(结果保留根号).