四川省泸州市泸县2021年数学中考一诊试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 方程 的根是( )A、 B、 C、 D、2. 已知关于 的方程 的一个根是-1,则 的值是( )A、-2 B、-1 C、1 D、23. 下利事件中,是必然事件的是( )A、将油滴在水中,油会浮在水面上 B、车辆随机到达一个路口,遇到红灯 C、如果 ,那么 D、掷一枚质地均匀的硬币,一定正面向上4. 下面4个图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 将一元二次方程 配方,其正确的结果是( )A、 B、 C、 D、6. 抛物线 的顶点坐标是( )A、 B、 C、 D、7. 从 ,0, ,3.14, 这5个数中随机抽取一个数,抽到有理数的概率是( )A、 B、 C、 D、8. 如图,点 、 、 在⊙O上, ,则 的度数是( )
5. 将一元二次方程 配方,其正确的结果是( )A、 B、 C、 D、6. 抛物线 的顶点坐标是( )A、 B、 C、 D、7. 从 ,0, ,3.14, 这5个数中随机抽取一个数,抽到有理数的概率是( )A、 B、 C、 D、8. 如图,点 、 、 在⊙O上, ,则 的度数是( ) A、 B、 C、 D、9. 如图, 是⊙O的切线,切点为 , , ,则⊙O的半径长为( )
A、 B、 C、 D、9. 如图, 是⊙O的切线,切点为 , , ,则⊙O的半径长为( )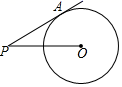 A、1 B、 C、2 D、310. 如图,已知 中, , , ,将 绕顶点 顺时针旋转至 的位置,且 、 、 三点在同一条直线上,则点 经过的路线的长度是( )
A、1 B、 C、2 D、310. 如图,已知 中, , , ,将 绕顶点 顺时针旋转至 的位置,且 、 、 三点在同一条直线上,则点 经过的路线的长度是( ) A、8 B、 C、 D、11. 关于 的一元二次方程 有两个实数根 , ,则代数式 的最小值是( )A、-8 B、-5 C、1 D、212. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
A、8 B、 C、 D、11. 关于 的一元二次方程 有两个实数根 , ,则代数式 的最小值是( )A、-8 B、-5 C、1 D、212. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. ⊙O的半径为 ,则⊙O的内接正方形的面积是 .14. 抛物线 向右平移2个单位,再向上平移3个单位得到的抛物线的解析式是.15. 如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是.
 16. 如图是二次函数 图象的一部分,其对称轴为直线 ,若其与 轴一交点为 ,则由图象可知,方程 的解是.
16. 如图是二次函数 图象的一部分,其对称轴为直线 ,若其与 轴一交点为 ,则由图象可知,方程 的解是.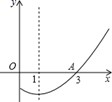
三、解答题
-
17. 解方程: .18. 已知关于x的一元二次方程 有实数根.(1)、求m的取值范围;(2)、当m为负整数时,求方程的两个根.19. 如图, 是⊙O的内接等边三角形,弦 交 于点 ,连接 .
 (1)、求 的度数;(2)、若 , ,求 的长.20. 如图,正方形网格中, 为格点三角形(顶点都是格点),将 绕点 按逆时针方向旋转 得到 .
(1)、求 的度数;(2)、若 , ,求 的长.20. 如图,正方形网格中, 为格点三角形(顶点都是格点),将 绕点 按逆时针方向旋转 得到 . (1)、在正方形网格中,作出 ;(不要求写作法)(2)、设网格小正方形的边长为 ,求线段 所扫过的图形的面积.(结果保留 )21. 某服装经营户以20元/件的价格购进一批衣服,以30元/件的价格出售,每天可售出20件.为了促销,该经营户决定降价销售,经调查发现,这种衣服每件降价1元,每天可多售出5件.另外,每天的房租等固定成本共25元,该经营户要想每天盈利200元,应将每件衣服的售价降低多少元?22. 如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度 (单位: )与飞行时间 (单位: )之间具有函数关系 ,请根据要求解答下列问题:
(1)、在正方形网格中,作出 ;(不要求写作法)(2)、设网格小正方形的边长为 ,求线段 所扫过的图形的面积.(结果保留 )21. 某服装经营户以20元/件的价格购进一批衣服,以30元/件的价格出售,每天可售出20件.为了促销,该经营户决定降价销售,经调查发现,这种衣服每件降价1元,每天可多售出5件.另外,每天的房租等固定成本共25元,该经营户要想每天盈利200元,应将每件衣服的售价降低多少元?22. 如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度 (单位: )与飞行时间 (单位: )之间具有函数关系 ,请根据要求解答下列问题: (1)、在飞行过程中,小球从飞出到落地所用时间是多少?(2)、在飞行过程中,小球飞行高度何时最大?最大高度是多少?23. 某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)、在飞行过程中,小球从飞出到落地所用时间是多少?(2)、在飞行过程中,小球飞行高度何时最大?最大高度是多少?23. 某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: (1)、本次调查的学生共有人,在扇形统计图中,m的值是;(2)、将条形统计图补充完整;(3)、在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.24. 如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)、本次调查的学生共有人,在扇形统计图中,m的值是;(2)、将条形统计图补充完整;(3)、在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.24. 如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.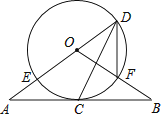 (1)、求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;(2)、求CD的长.25. 如图,抛物线 经过 、 、 三点,对称轴与抛物线相交于点 ,与直线 相交于点 ,连接 , .
(1)、求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;(2)、求CD的长.25. 如图,抛物线 经过 、 、 三点,对称轴与抛物线相交于点 ,与直线 相交于点 ,连接 , . (1)、求该抛物线的解析式;(2)、设对称轴与 轴交于点 ,在对称轴上是否存在点 ,使以 、 、 为顶点的三角形与 相似?如果存在,请求出点 的坐标;如果不存在,请说明理由;(3)、抛物线上是否存在一点 ,使 与 的面积相等,若存在,求点 的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、设对称轴与 轴交于点 ,在对称轴上是否存在点 ,使以 、 、 为顶点的三角形与 相似?如果存在,请求出点 的坐标;如果不存在,请说明理由;(3)、抛物线上是否存在一点 ,使 与 的面积相等,若存在,求点 的坐标;若不存在,请说明理由.