四川省广安市岳池县2021年数学中考诊断试卷(三)
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. -2021的绝对值和相反数分别为( )A、2021, -2021 B、-2021,2021 C、2021,2021 D、-2021,-20212. 下列运算正确的是( )A、 B、 C、 D、3. 下列说法正确的是 ( )A、将3.10万用科学记数法表示为 B、若用科学记数法表示的数为 ,则其原数为20100 C、近似数2.3与2.30精确度相同 D、用四舍五入法将1.097精确到百分位为1.104. 如图是小华送给她外婆的生日蛋糕,则下面关于三种视图判断完全正确的是 ( )
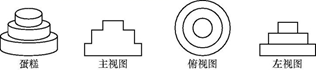 A、主视图、俯视图,左视图错误 B、俯视图、左视图正确,主视图错误 C、左视图、主视图正确,俯视图错误 D、主视图、俯视图,左视图都正确5. 下列说法正确的是( )A、某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖. B、为了解全国中学生的睡眠情况,应该采用普查的方式. C、若甲数据的方差s 甲 2 =0.05,乙数据的方差s 乙 2 =0.1,则乙数据比甲数据稳定. D、一组数据3,5,4,5,5,6,10的众数和中位数都是5.6. 《算经十书》是指汉、唐一千多年间的十部著名的数学著作,十部书的名称是:《周髀算经》、《九章算术》、《海岛算经》、《张丘建算经》、《夏侯阳算经》、《五经算术》、《缉古算经》、《缀术》、《五曹算经》、《孙子算经》.其中在《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余 尺;将绳子对折再量木条,木条剩余 尺,问绳子、木条长多少尺?”,设绳子长为 尺,木条长为 尺,根据题意,所列方程组正确的是( )A、 B、 C、 D、7. 下列命题是假命题的是( )A、在同圆或等圆中,同弧或等弧所对的圆周角相等 B、平分弦的直径垂直于弦 C、两条平行线间的距离处处相等 D、正方形的两条对角线互相垂直平分8. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、主视图、俯视图,左视图错误 B、俯视图、左视图正确,主视图错误 C、左视图、主视图正确,俯视图错误 D、主视图、俯视图,左视图都正确5. 下列说法正确的是( )A、某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖. B、为了解全国中学生的睡眠情况,应该采用普查的方式. C、若甲数据的方差s 甲 2 =0.05,乙数据的方差s 乙 2 =0.1,则乙数据比甲数据稳定. D、一组数据3,5,4,5,5,6,10的众数和中位数都是5.6. 《算经十书》是指汉、唐一千多年间的十部著名的数学著作,十部书的名称是:《周髀算经》、《九章算术》、《海岛算经》、《张丘建算经》、《夏侯阳算经》、《五经算术》、《缉古算经》、《缀术》、《五曹算经》、《孙子算经》.其中在《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余 尺;将绳子对折再量木条,木条剩余 尺,问绳子、木条长多少尺?”,设绳子长为 尺,木条长为 尺,根据题意,所列方程组正确的是( )A、 B、 C、 D、7. 下列命题是假命题的是( )A、在同圆或等圆中,同弧或等弧所对的圆周角相等 B、平分弦的直径垂直于弦 C、两条平行线间的距离处处相等 D、正方形的两条对角线互相垂直平分8. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、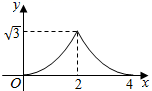 B、
B、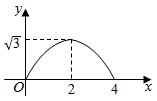 C、
C、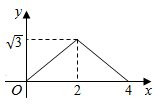 D、
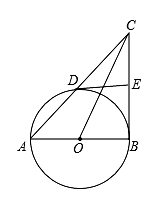
D、 9. 如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”;当AC=3,BC=4时,计算阴影部分的面积为( )
9. 如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”;当AC=3,BC=4时,计算阴影部分的面积为( )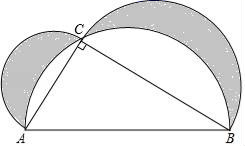 A、6 B、6π C、10π D、1210. 如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论:①abc>0;②4a﹣2b+c<0;③b2>4ac;④ax2+bx+c≥﹣6;⑤若点M(﹣2,m)与点N(﹣5,n)为抛物线上两点,则m>n;⑥关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1.其中正确结论有( )
A、6 B、6π C、10π D、1210. 如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论:①abc>0;②4a﹣2b+c<0;③b2>4ac;④ax2+bx+c≥﹣6;⑤若点M(﹣2,m)与点N(﹣5,n)为抛物线上两点,则m>n;⑥关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1.其中正确结论有( )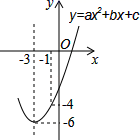 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
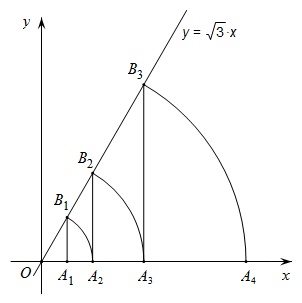
11. 如果点A( , )在第二象限,那么点B( , )在第象限。12. 因式分解: .13. 规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“雅系特征值”,记作k,若 ,则该等腰三角形的顶角为.14. 正六边形的边心距为 ,则该正六边形的边长是.15. 将抛物线 先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为.16. 如图,直线 ,点 坐标为 ,过点 作 轴的垂线交直线于点 ,以原点 为圆心, 长为半径画弧交 轴于点 ;再过点 作 轴的垂线交直线于点 ,以原点 为圆心, 长为半径画弧交 轴于点 ,…,按此做法进行下去,点 的坐标为.
三、解答题
-
17. 计算:(π﹣2)0﹣2cos30°﹣ +|1﹣ |.18. 先化简, ,然后从1,2,3中任选一个合适的 的值,代入求值.19. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
 (1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.20. 如图, 中, ,顶点A,B都在反比例函数 的图象上,直线 轴,垂足为D,连结 , ,并延长 交 于点E,当 时,点E恰为 的中点,若 , .
(1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.20. 如图, 中, ,顶点A,B都在反比例函数 的图象上,直线 轴,垂足为D,连结 , ,并延长 交 于点E,当 时,点E恰为 的中点,若 , .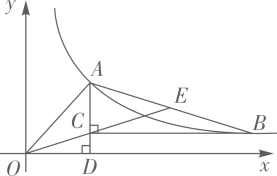 (1)、求反比例函数的解析式;(2)、求 的度数.21. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.
(1)、求反比例函数的解析式;(2)、求 的度数.21. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.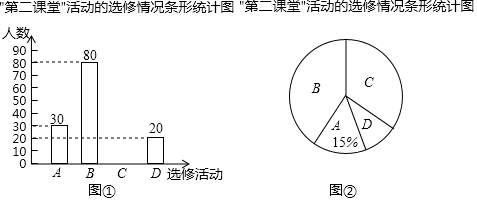
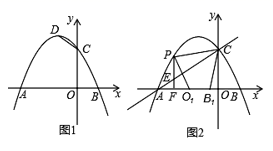
根据图中提供的信息,解答下列问题:
(1)、本次调查的学生共有人;在扇形统计图中,B所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.22. 有一家苗圃计划种植桃树和柏树,根据市场调查与预测,种植桃树的利润y1(万元)与投资成本x(万元)满足如图1所示的二次函数y1=ax2;种植柏树的利润y2(万元)与投资成本x(万元)满足如图2所示的正比例函数y2=kx .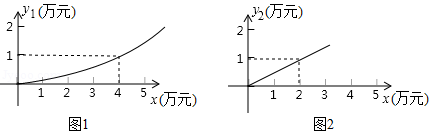 (1)、请分别直接写出利润y1(万元)与利润y2(万元)关于投资成本x(万元)的函数关系式;(2)、若这家苗圃投资4万元种植桃树,投资6万元种植柏树,则可获得的总利润是多少万元?(3)、若这家苗圃种植桃树和柏树投入总成本20万元,且桃树的投资成本不低于2万元,且不高于12万元,则苗圃最少能获得多少总利润?最多可获得多少总利润?23. 疫情期间,为了保障大家的健康,各地采取了多种方式进行预防,某地利用无人机规劝居民回家.如图,一条笔直的街道 ,在街道 处的正上方 处有一架无人机,该无人机在 处测得俯角为 的街道 处有人聚集,然后沿平行于街道 的方向再向前飞行60米到达 处,在 处测得俯角为 的街道 处也有人聚集,已知两处聚集点 之间的距离为120米,求无人机飞行的高度 .(参考数据: , , , )
(1)、请分别直接写出利润y1(万元)与利润y2(万元)关于投资成本x(万元)的函数关系式;(2)、若这家苗圃投资4万元种植桃树,投资6万元种植柏树,则可获得的总利润是多少万元?(3)、若这家苗圃种植桃树和柏树投入总成本20万元,且桃树的投资成本不低于2万元,且不高于12万元,则苗圃最少能获得多少总利润?最多可获得多少总利润?23. 疫情期间,为了保障大家的健康,各地采取了多种方式进行预防,某地利用无人机规劝居民回家.如图,一条笔直的街道 ,在街道 处的正上方 处有一架无人机,该无人机在 处测得俯角为 的街道 处有人聚集,然后沿平行于街道 的方向再向前飞行60米到达 处,在 处测得俯角为 的街道 处也有人聚集,已知两处聚集点 之间的距离为120米,求无人机飞行的高度 .(参考数据: , , , )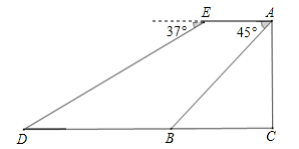 24. 如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
24. 如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.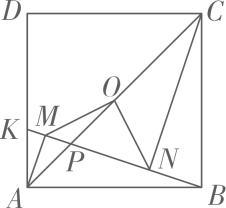 (1)、求证:AM=BN;(2)、请判断△OMN的形状,并说明理由;(3)、若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为 ,请直接写出AK长.
(1)、求证:AM=BN;(2)、请判断△OMN的形状,并说明理由;(3)、若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为 ,请直接写出AK长.