四川省成都市邛崃市2021年数学中考二诊试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 下列四个数中,比 大的数是( )A、-2 B、-1 C、0 D、-π2. 如图所示的几何体,其左视图是( )
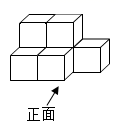 A、
A、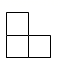 B、
B、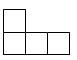 C、
C、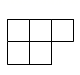 D、
D、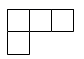 3. 据搜狐网报道,2019年五一节期间,国内各大旅游景区人气爆棚,成都作为“博物馆之城”,各大博物馆都“人从众”,特别是亲子类家庭选择到博物馆里打卡,各大博物馆的人气丝毫不亚于5A级景区.截至5月4日晚6点,记者从成都六大博物馆获悉,小长假期间,累计有68.9万人次走进博物馆.68.9万用科学记数法表示为( )A、 B、 C、 D、4. 如图, , , ,则 ( )
3. 据搜狐网报道,2019年五一节期间,国内各大旅游景区人气爆棚,成都作为“博物馆之城”,各大博物馆都“人从众”,特别是亲子类家庭选择到博物馆里打卡,各大博物馆的人气丝毫不亚于5A级景区.截至5月4日晚6点,记者从成都六大博物馆获悉,小长假期间,累计有68.9万人次走进博物馆.68.9万用科学记数法表示为( )A、 B、 C、 D、4. 如图, , , ,则 ( )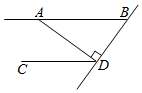 A、32° B、45° C、58° D、68°5. 如图,在平面直角坐标系中,已知点 , ,平移线段 ,使点 落在点 处,则点 对应的点 的坐标为( )
A、32° B、45° C、58° D、68°5. 如图,在平面直角坐标系中,已知点 , ,平移线段 ,使点 落在点 处,则点 对应的点 的坐标为( )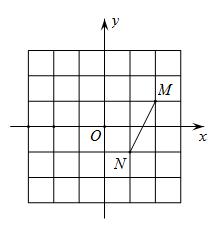 A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 某学校为了解九年级学生的体育达标情况,随机抽取40名九年级学生进行体育测试,测试成绩如下:
A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 某学校为了解九年级学生的体育达标情况,随机抽取40名九年级学生进行体育测试,测试成绩如下:测试成绩(分)
40
42
44
46
48
49
50
人数(人)
2
3
6
10
12
3
4
则本次抽测中体育成绩的众数和中位数分别是( )
A、12和4 B、48和46 C、4和12 D、46和488. 如图, 是 的直径,弦 ,垂足为 .若 , 的半径是5,则弦 的长是( )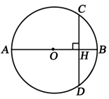 A、8 B、4 C、10 D、9. 某果品分拣车间有甲、乙两组工人负责将猕猴桃装箱,已知每小时甲组比乙组少装16箱,甲组装260箱与乙组装340箱所用的时间相等,设甲组每小时装 箱,所列方程正确的是( )A、 B、 C、 D、10. 如图,抛物线 与 轴交于点 ,其对称轴为直线 ,结合图象分析下列结论,其中正确的结论是( )
A、8 B、4 C、10 D、9. 某果品分拣车间有甲、乙两组工人负责将猕猴桃装箱,已知每小时甲组比乙组少装16箱,甲组装260箱与乙组装340箱所用的时间相等,设甲组每小时装 箱,所列方程正确的是( )A、 B、 C、 D、10. 如图,抛物线 与 轴交于点 ,其对称轴为直线 ,结合图象分析下列结论,其中正确的结论是( )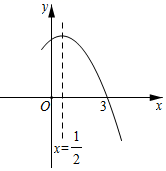 A、 B、 C、当 时, 随 的增大而减小 D、
A、 B、 C、当 时, 随 的增大而减小 D、二、填空题
-
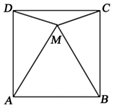
11. 若 ,则 .12. 若一次函数 的图象经过第一、二、四象限,则 0.13. 如图,在正方形 的内部作等边 ,连接 、 ,则 .
 14. 如图,菱形 中,分别以点 、 为圆心,大于 长为半径作弧,两弧分别交于点 、 ,作直线 ,且直线 恰好经过点 ,与边 交于点 .连接 ,若 ,则 .
14. 如图,菱形 中,分别以点 、 为圆心,大于 长为半径作弧,两弧分别交于点 、 ,作直线 ,且直线 恰好经过点 ,与边 交于点 .连接 ,若 ,则 . 15. 已知代数式 的值为6,则代数式 的值为.16. 关于 的分式方程 的解为非负数,则 的取值范围是.17. 关于 的方程 有两个相等的实数根,其中 是锐角 的一个内角;关于 的方程 的两个根恰好是 的两边长,则 的周长是.18. 如图,在 中, , , ,点 在 内,连接 、 、 ,则 的最小值是.
15. 已知代数式 的值为6,则代数式 的值为.16. 关于 的分式方程 的解为非负数,则 的取值范围是.17. 关于 的方程 有两个相等的实数根,其中 是锐角 的一个内角;关于 的方程 的两个根恰好是 的两边长,则 的周长是.18. 如图,在 中, , , ,点 在 内,连接 、 、 ,则 的最小值是.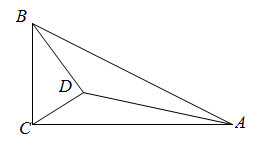 19. 如图,在平面直角坐标系 中,直线 : 和反比例函数 的图象交于第二象限的点 ,点 是射线 上一点,过点 作 轴、 轴的垂线,分别交函数 的图象于点 , .由线段 , 和函数 的图象在点 , 之间的部分所围成的区域(不含边界)记为 .若区域 内恰有5个整点,则 的取值范围是.(注:横、纵坐标都是整数的点叫做整点)
19. 如图,在平面直角坐标系 中,直线 : 和反比例函数 的图象交于第二象限的点 ,点 是射线 上一点,过点 作 轴、 轴的垂线,分别交函数 的图象于点 , .由线段 , 和函数 的图象在点 , 之间的部分所围成的区域(不含边界)记为 .若区域 内恰有5个整点,则 的取值范围是.(注:横、纵坐标都是整数的点叫做整点)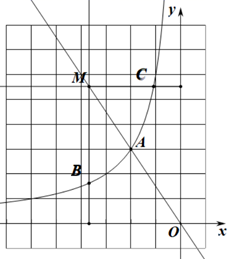
三、解答题
-
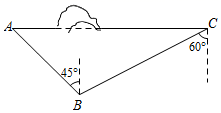
20. 计算:(1)、 .(2)、解不等式组 .21. 化简 .22. 如图, 地在 地的正东方向,由于大山的阻隔,从 地到 地需要绕行 地、已知 地位于 地的南偏西60方向, 地距离 地200千米, 地位于 地的北偏西45°方向.现准备打通 、 两地的穿山隧道,修建 、 两地的直达高速公路.求 地到 地之间高速公路 的长(结果保留根号).
 23. 教育青少年热爱劳动,养成爱劳动的习惯,培养德智体美劳全面发展的社会主义建设者和接班人,是当今教育的重要任务之一.学校要求学生寒假期间在家帮助父母做一些力所能及的家务.开学初,张亮同学随机调查了九年级部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为 小时,将做家务的总时间分为五个类别: , , , , ,并将调查结果绘制成如下两幅不完整的统计图:
23. 教育青少年热爱劳动,养成爱劳动的习惯,培养德智体美劳全面发展的社会主义建设者和接班人,是当今教育的重要任务之一.学校要求学生寒假期间在家帮助父母做一些力所能及的家务.开学初,张亮同学随机调查了九年级部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为 小时,将做家务的总时间分为五个类别: , , , , ,并将调查结果绘制成如下两幅不完整的统计图: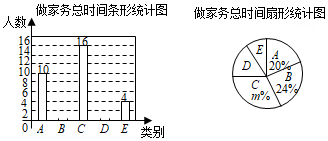
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;扇形统计图中 ;(2)、根据以上信息直接在答题卡上补全条形统计图;(3)、设 类4个学生为 , , , ,若要从其中抽取2名学生参加学校组织的公益劳动,请用列表或画树状图的方法求恰好抽到 , 的概率.24. 如图,在平面直角坐标系 中,反比例函数 与一次函数 的图象交于 、 两点,且 ;直线 与反比例函数 的图象交于另一点 ,过点 作 轴的平行线,交 轴于点 ,过点 作 轴的平行线,两直线交于点 .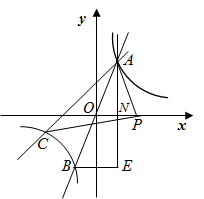 (1)、求反比例函数 的表达式及 的面积;(2)、若 是 轴上一点,当 的面积是 面积的2倍时,求点 的坐标.25. 如图,以 的边 上一点 作 经过点 ,交 于点 .连接 ,作 交 于点 ,交 于点 ,连接 交 于点 .
(1)、求反比例函数 的表达式及 的面积;(2)、若 是 轴上一点,当 的面积是 面积的2倍时,求点 的坐标.25. 如图,以 的边 上一点 作 经过点 ,交 于点 .连接 ,作 交 于点 ,交 于点 ,连接 交 于点 .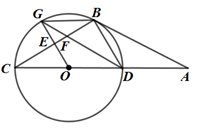 (1)、当 时,求证: 为 的切线;(2)、若 , ,求 的长;(3)、若 ,求 的值.26. 今年甲、乙两个果园的红心猕猴桃喜获丰收,已知甲果园的总产量为27吨,乙果园的总产量13吨,某果业公司租用 、 两种型号的保鲜货车去果园运输猕猴桃,甲果园需要 型保鲜货车满载猕猴桃运输6趟,同时需要 型保鲜货车满载猕猴桃运输5趟才能刚好运输完:乙果园需 型保鲜货车满载猕猴桃运输2趟,同时需要 型保鲜货车满载猕猴桃运输3趟刚好运输完.(1)、求 、 两种保鲜货车满载猕猴桃运输一趟分别是多少吨?(2)、果业公司收购该批猕猴桃的单价为0.8万元/吨,目前公司可以0.9万元/吨的价格售出,如果保鲜冷藏储存起来,旺市再销售以便获取最大利润,由于失水和腐烂,水果重量每天减少0.5吨,且每天需支付各种费用0.08万元/吨,而每天的价格会持续上涨0.1万元/吨、如果公司计划把该批猕猴桃最多保鲜冷藏储存20天,那么储存多少天后出售这批猕猴桃所获得的利润最大?最大利润是多少万元?27. 已知在 中, , , ,将 绕点 逆时针旋转 得到 ,直线 交 于点 , 交 于点 .
(1)、当 时,求证: 为 的切线;(2)、若 , ,求 的长;(3)、若 ,求 的值.26. 今年甲、乙两个果园的红心猕猴桃喜获丰收,已知甲果园的总产量为27吨,乙果园的总产量13吨,某果业公司租用 、 两种型号的保鲜货车去果园运输猕猴桃,甲果园需要 型保鲜货车满载猕猴桃运输6趟,同时需要 型保鲜货车满载猕猴桃运输5趟才能刚好运输完:乙果园需 型保鲜货车满载猕猴桃运输2趟,同时需要 型保鲜货车满载猕猴桃运输3趟刚好运输完.(1)、求 、 两种保鲜货车满载猕猴桃运输一趟分别是多少吨?(2)、果业公司收购该批猕猴桃的单价为0.8万元/吨,目前公司可以0.9万元/吨的价格售出,如果保鲜冷藏储存起来,旺市再销售以便获取最大利润,由于失水和腐烂,水果重量每天减少0.5吨,且每天需支付各种费用0.08万元/吨,而每天的价格会持续上涨0.1万元/吨、如果公司计划把该批猕猴桃最多保鲜冷藏储存20天,那么储存多少天后出售这批猕猴桃所获得的利润最大?最大利润是多少万元?27. 已知在 中, , , ,将 绕点 逆时针旋转 得到 ,直线 交 于点 , 交 于点 .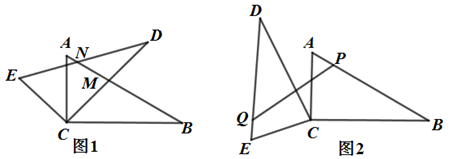 (1)、如图1,求证: ;(2)、如图2,当 时, 为线段 上一动点,旋转后点 的对应点为点 ,求线段 的最小值:(3)、在旋转过程中,满足 是等腰三角形时,直接写出点 所旋转的路径长(结果保留 ).28. 如图,抛物线 与 轴交于点 , ,与 轴交于点 ,且顶点的纵坐标为9
(1)、如图1,求证: ;(2)、如图2,当 时, 为线段 上一动点,旋转后点 的对应点为点 ,求线段 的最小值:(3)、在旋转过程中,满足 是等腰三角形时,直接写出点 所旋转的路径长(结果保留 ).28. 如图,抛物线 与 轴交于点 , ,与 轴交于点 ,且顶点的纵坐标为9 (1)、求抛物线的解析式;(2)、如图1,点 在线段 上运动,过点 作直线 轴,交抛物线于点 ,交直线 于点 ,若以 、 、 为顶点的三角形与 相似,求点 的坐标:(3)、如图2,点 在抛物线的对称轴上,过点 作 轴交直线 于点 ,连接 、 ,点 是 的中点,点 是线段 上任意一点,将 沿 边翻折得到 ,且点 落在直线 的上方,求当线段 的长为何值时, 与 重叠部分的面积是 面积的 ?
(1)、求抛物线的解析式;(2)、如图1,点 在线段 上运动,过点 作直线 轴,交抛物线于点 ,交直线 于点 ,若以 、 、 为顶点的三角形与 相似,求点 的坐标:(3)、如图2,点 在抛物线的对称轴上,过点 作 轴交直线 于点 ,连接 、 ,点 是 的中点,点 是线段 上任意一点,将 沿 边翻折得到 ,且点 落在直线 的上方,求当线段 的长为何值时, 与 重叠部分的面积是 面积的 ?