四川省成都市青羊区2021年数学中考二诊试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 2021 B、﹣2021 C、 D、±20212. 下列四个立体图形中,它们各自的三视图都相同的是( )A、
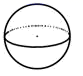 B、
B、 C、
C、 D、
D、 3. 2020年6月23日,中国第55颗北斗导航卫星成功发射,标志着拥有全球知识产权的北斗导航系统全面建成,据统计:2019年,我国北斗卫星导航与位置服务产业总体产值达3450亿元,较2018年增长14.4%,其中,3450亿用科学记数法表示为( )元.A、 B、 C、 D、4. 代数式 , 的取值范围是( )A、 B、 C、 D、5. 已知正比例函数 的图象过点 ,把正比例函数 的图象平移,使它过点 ,则平移后的函数图象大致是( )A、
3. 2020年6月23日,中国第55颗北斗导航卫星成功发射,标志着拥有全球知识产权的北斗导航系统全面建成,据统计:2019年,我国北斗卫星导航与位置服务产业总体产值达3450亿元,较2018年增长14.4%,其中,3450亿用科学记数法表示为( )元.A、 B、 C、 D、4. 代数式 , 的取值范围是( )A、 B、 C、 D、5. 已知正比例函数 的图象过点 ,把正比例函数 的图象平移,使它过点 ,则平移后的函数图象大致是( )A、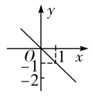 B、
B、 C、
C、 D、
D、 6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,四边形 是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得 ,下列不正确的是( )
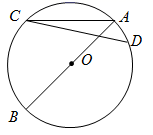
6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,四边形 是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得 ,下列不正确的是( )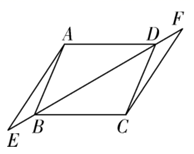 A、 B、 C、 D、8. 有一组数据:1,2,3,6,这组数据的方差是( )A、2.5 B、3 C、3.5 D、49. 如图, 是 的直径,点C是 延长线上一点, 与 相切于点P,连接 ,若 , ,则 的长是( )
A、 B、 C、 D、8. 有一组数据:1,2,3,6,这组数据的方差是( )A、2.5 B、3 C、3.5 D、49. 如图, 是 的直径,点C是 延长线上一点, 与 相切于点P,连接 ,若 , ,则 的长是( )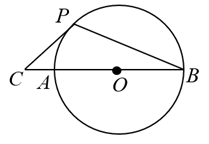 A、 B、 C、 D、10. 下列关于二次函数 的说法,正确的是( )A、对称轴是直线 B、当 时有最小值 C、顶点坐标是 D、当 时,y随x的增大而减少
A、 B、 C、 D、10. 下列关于二次函数 的说法,正确的是( )A、对称轴是直线 B、当 时有最小值 C、顶点坐标是 D、当 时,y随x的增大而减少二、填空题
-
11. 因式分解: .12. 如图, 是 的直径, ,则 度.
 13. 从线段、等边三角形、平行四边形、圆、双曲线、抛物线中随机抽取两个(不放回),得到的图形都是中心对称图形的概率是.14. 如图,线段 ,用尺规作图法按如下步骤作图.
13. 从线段、等边三角形、平行四边形、圆、双曲线、抛物线中随机抽取两个(不放回),得到的图形都是中心对称图形的概率是.14. 如图,线段 ,用尺规作图法按如下步骤作图.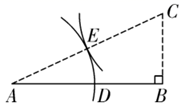
( 1 )过点B作 的垂线,并在垂线上取 ;
( 2 )连接 ,以点C为圆心, 为半径画弧,交 于点E;
( 3 )以点A为圆心, 为半径画弧,交 于点D.即点D为线段 的黄金分割点.
则线段 的长度约为
(结果保留两位小数,参考数据: )
15. 已知k是 的小数部分,则 .16. 若m、n是方程 的两个实数根,则 之值为.17. 如图,正方形 与正方形 的边 、 均在x轴上,点F在 边上,反比例函数 的图象经过点A、E,且 ,则 . 18. 如图,在平面直角坐标系中,点Q是一次函数 的图象上一动点,将Q绕点 顺时针旋转 到点P,连接 ,则 的最小值.
18. 如图,在平面直角坐标系中,点Q是一次函数 的图象上一动点,将Q绕点 顺时针旋转 到点P,连接 ,则 的最小值.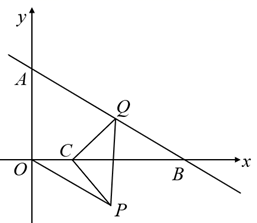 19. 如图,在 中, , ,将 绕点A顺时针旋转 得到 ,直线 、 交于点D,则 的长为.
19. 如图,在 中, , ,将 绕点A顺时针旋转 得到 ,直线 、 交于点D,则 的长为.
三、解答题
-
20.(1)、计算: .(2)、解不等式组 .21. 解分式方程: .22. 如图,在一个坡度(或坡比) 的山坡 上发现有一棵古树 .测得古树底端C到山脚点A的距离 米,在距山脚点A水平距离4米的点E处,测得古树顶端D的仰角 (古树 与山坡 的剖面、点E在同一平面上,古树 与直线 垂直),求古树 的高度.(结果保留两位小数)(参考数据: )
 23. 为庆祝中国共产党建党100周年,我区某校组织全校2100名学生进行了党史知识竞赛,参赛学生均获奖.为了解本次竞赛获奖的分布情况,从中随机抽取了部分学生的获奖结果进行统计分析,获奖结果分为四个等级:A级为特等奖,B级为一等奖,C级为二等奖,D级为三等奖,将统计结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题:
23. 为庆祝中国共产党建党100周年,我区某校组织全校2100名学生进行了党史知识竞赛,参赛学生均获奖.为了解本次竞赛获奖的分布情况,从中随机抽取了部分学生的获奖结果进行统计分析,获奖结果分为四个等级:A级为特等奖,B级为一等奖,C级为二等奖,D级为三等奖,将统计结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题: (1)、本次被抽取的部分人数是名;(2)、扇形统计图中表示B级的扇形圆心角的度数是 ▲ ,并把条形统计图补充完整;(3)、根据抽样结果,请估计该校获得特等奖的人数为名;(4)、某班有4名获特等奖的学生小利、小芳、小明、小亮,班主任要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求小利被选中的概率.24. 如图,函数 (k为常数, )的图象与过原点O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线 分别交x轴、y轴于C、D两点,连接 分别交x轴、y轴于点E、F.
(1)、本次被抽取的部分人数是名;(2)、扇形统计图中表示B级的扇形圆心角的度数是 ▲ ,并把条形统计图补充完整;(3)、根据抽样结果,请估计该校获得特等奖的人数为名;(4)、某班有4名获特等奖的学生小利、小芳、小明、小亮,班主任要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求小利被选中的概率.24. 如图,函数 (k为常数, )的图象与过原点O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线 分别交x轴、y轴于C、D两点,连接 分别交x轴、y轴于点E、F.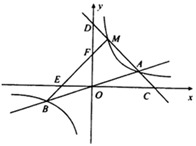 (1)、若直线 的解析式为 ,A点的坐标为 ,则当 时,求直线 的解析式;(2)、若 ,求 的值.25. 如图, 为 的直径,C为 上一点,连接 ,D是 上的一点,CD=BD, 与 、 分别交于点E、F.
(1)、若直线 的解析式为 ,A点的坐标为 ,则当 时,求直线 的解析式;(2)、若 ,求 的值.25. 如图, 为 的直径,C为 上一点,连接 ,D是 上的一点,CD=BD, 与 、 分别交于点E、F. (1)、求证: ;(2)、求证: ;(3)、若 ,求 的值.26. 在精准扶贫过程中,某土特产公司组织20辆汽车装运A、B、C三种土特产共150吨去外地销售,按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据如表提供的信息,解答以下问题:
(1)、求证: ;(2)、求证: ;(3)、若 ,求 的值.26. 在精准扶贫过程中,某土特产公司组织20辆汽车装运A、B、C三种土特产共150吨去外地销售,按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据如表提供的信息,解答以下问题:土特产品种
A
B
C
每辆汽车运载量(吨)
10
8
6
每吨土特产获利(百元)
14
18
10
(1)、设装运A种土特产的车辆数为x,装运B种土特产的车辆数为y,求y与x之间的函数关系式;(2)、如果装运每种土特产的车辆都不少于3辆,若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.27. 如图 (1)、如图1,四边形 是正方形,点E、F分别是边 上的点,连接线段 , ,试判断 之间的关系,并说明理由;(2)、如图2,四边形 是菱形,点E、F分别是边 上的点,连接线段 , ,试说明 ;(3)、如图3,若菱形的边长为 ,点E在 的延长线上, ,求线段 的长.28. 如图,二次函数 的图象与x轴、y轴交于点 、 、C三点,点P是抛物线位于一象限内图象上的一点.
(1)、如图1,四边形 是正方形,点E、F分别是边 上的点,连接线段 , ,试判断 之间的关系,并说明理由;(2)、如图2,四边形 是菱形,点E、F分别是边 上的点,连接线段 , ,试说明 ;(3)、如图3,若菱形的边长为 ,点E在 的延长线上, ,求线段 的长.28. 如图,二次函数 的图象与x轴、y轴交于点 、 、C三点,点P是抛物线位于一象限内图象上的一点. (1)、求二次函数的解析式;(2)、作点P关于直线 的对称点D,求四边形 面积的最大值;(3)、在(2)的条件下,连接线段 ,将线段 绕点C逆时针旋转 到 ,连接 交抛物线于点F,交直线 于点G,试求当 为直角三角形时点F的坐标.
(1)、求二次函数的解析式;(2)、作点P关于直线 的对称点D,求四边形 面积的最大值;(3)、在(2)的条件下,连接线段 ,将线段 绕点C逆时针旋转 到 ,连接 交抛物线于点F,交直线 于点G,试求当 为直角三角形时点F的坐标.