四川省成都市都江堰市2021年数学中考二诊试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 两个负数相加,其和一定是( )A、正数 B、负数 C、非负数 D、02. 目前,我国“新冠”疫苗接种正在有序推进.国家卫生健康委员会公布的数据显示,截至2021年4月20日,全国各地累计报告接种新冠病毒疫苗已超过19500万剂次,将数据“19500万”用科学记数法可表示为( )A、 B、 C、 D、3. 如图是由5个大小相同的小正方体摆成的几何体,它的俯视图是( )
 A、
A、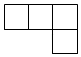 B、
B、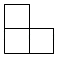 C、
C、 D、
D、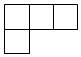 4. 下列计算正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,已知点 在第二象限,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在正方形点阵中,相邻的四个点构成正方形.图中线段的端点都在点阵上,则图中线段形成的角中与 相等(不包括 )的角有( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 在平面直角坐标系中,已知点 在第二象限,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在正方形点阵中,相邻的四个点构成正方形.图中线段的端点都在点阵上,则图中线段形成的角中与 相等(不包括 )的角有( ) A、1个 B、2个 C、3个 D、4个7. 如图,某学校篮球队12名队员的年龄情况如条形统计图所示,则12名队员年龄的中位数是( )
A、1个 B、2个 C、3个 D、4个7. 如图,某学校篮球队12名队员的年龄情况如条形统计图所示,则12名队员年龄的中位数是( ) A、13 B、14 C、15 D、168. 一个边长为2厘米的正方形,如果它的边长增加 厘米,则面积随之增加 平方厘米,那么 与 之间满足的函数关系是( )A、正比例函数 B、反比例函数 C、一次函数 D、二次函数9. 如图,已知 ,用直尺和圆规按照以下步骤作图:
A、13 B、14 C、15 D、168. 一个边长为2厘米的正方形,如果它的边长增加 厘米,则面积随之增加 平方厘米,那么 与 之间满足的函数关系是( )A、正比例函数 B、反比例函数 C、一次函数 D、二次函数9. 如图,已知 ,用直尺和圆规按照以下步骤作图:
①以点 为圆心,任意长为半径画弧,分别交 、 于点 、 ;
②画射线 ,以点 为圆心, 长为半径画弧,交 于点 ;
③以点 为圆心, 长为半径画弧,与第②步中所画的弧相交于点 ;
④过点 画射线 ;
根据以上操作,可以判定 ≌ ,其判定的依据是( )
A、SSS B、SAS C、ASA D、HL10. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )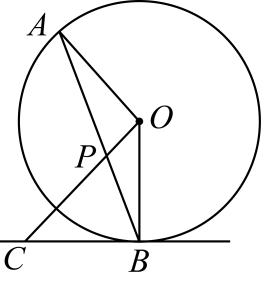 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
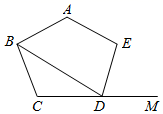
11. 如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.
 12. 分式方程 的解为.13. 如图,已知某一条传送带的转动轮的半径为30厘米.如果该转动轮转动120°,那么传送带上的物品 被传送厘米.(结果保留π)
12. 分式方程 的解为.13. 如图,已知某一条传送带的转动轮的半径为30厘米.如果该转动轮转动120°,那么传送带上的物品 被传送厘米.(结果保留π) 14. 二次函数 的图象如图所示,则下列四个结论:
14. 二次函数 的图象如图所示,则下列四个结论:① ;② ;③ ;④ .其中正确的有.(填写番号)
 15. 已知 ,那么 .(用含 的代数式表示)16. 已知下列四个图形:①长度为 的线段;②斜边为3的直角三角形;③面积为4的菱形;④半径为 ,圆心角为90°的扇形;其中,能够被半径为1的圆及其内部所覆盖的图形是.(填写序号)17. 如图,在平面直角坐标系 中,P是直线 上的一个动点, 的半径为1,直线 切 于点Q,则线段 的最小值为.
15. 已知 ,那么 .(用含 的代数式表示)16. 已知下列四个图形:①长度为 的线段;②斜边为3的直角三角形;③面积为4的菱形;④半径为 ,圆心角为90°的扇形;其中,能够被半径为1的圆及其内部所覆盖的图形是.(填写序号)17. 如图,在平面直角坐标系 中,P是直线 上的一个动点, 的半径为1,直线 切 于点Q,则线段 的最小值为.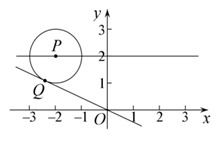 18. 如图,在平面直角坐标系中,已知直线 和双曲线 ,在直线上取一点,记为 ,过点 作 轴的垂线交双曲线于点 ,过点 作 轴的垂线交直线于点 ,过点 作 轴的垂线交双曲线于点 ,过点 作 轴的垂线交直线于点 ,…依次进行下去,记点 的横坐标为 ,若 ,则 .
18. 如图,在平面直角坐标系中,已知直线 和双曲线 ,在直线上取一点,记为 ,过点 作 轴的垂线交双曲线于点 ,过点 作 轴的垂线交直线于点 ,过点 作 轴的垂线交双曲线于点 ,过点 作 轴的垂线交直线于点 ,…依次进行下去,记点 的横坐标为 ,若 ,则 . 19. 如图,在 中,已知 是 边上的中线, , .将 沿直线 翻折,点 落在平面上的点 处,连接 交 于点 ,那么 的值为.
19. 如图,在 中,已知 是 边上的中线, , .将 沿直线 翻折,点 落在平面上的点 处,连接 交 于点 ,那么 的值为.
三、解答题
-
20.(1)、计算: ;(2)、先化简,再求值: ,其中 .21. 解不等式组: .22. 从2022年起,成都市中考体育将实施新的方案.新方案规定:体育统一考试由“必考项目”和“选考项目”组成;其中,男生的“选考项目”有两项,由男生在下列两类选考类别中各选一项组成:
选考类别
选考项目
第一类(三选一)
A:足球运球
B:排球垫球
C:篮球上篮
第二类(二选一)
D:引体向上
E:投掷实心球
(1)、某男生从第一类选考类别中随机选择一个项目,选中足球运球的概率为.(2)、用树状图或列表法表示:男生的两项“选考项目”所有可能出现的结果;(3)、求事件“一名男生随机确定两项选考项目,其中有引体向上”发生的概率.23. 如图,某游乐场有一个直径为100米的摩天轮转盘,其最高点距离地面高度为110米,该摩天轮匀速转动一周的时间为24分钟,摩天轮上的吊舱每分钟转过的角度相同.某游客乘坐吊舱从转盘上最低点 出发,2分钟后到达点 处. (1)、求 的度数;(2)、求此时吊舱所在的位置点 距离地面的高度约为多少米?(结果精确到 )(参考数据: , )24. 如图,平面直角坐标系中,双曲线 与直线 相交于点 .
(1)、求 的度数;(2)、求此时吊舱所在的位置点 距离地面的高度约为多少米?(结果精确到 )(参考数据: , )24. 如图,平面直角坐标系中,双曲线 与直线 相交于点 . (1)、求 、 的值;(2)、点 是双曲线 上一点,且 与直线 平行;
(1)、求 、 的值;(2)、点 是双曲线 上一点,且 与直线 平行;①求点 的横坐标;
②请直接写出点 到直线 的距离.
25. 如图,⊙O的直径 ,点 为弧 上一点,连接 、 ,点 为劣弧 上一点(点 不与点 、 重合),连接 交 、 于点 、 .
 (1)、当 时, 的长度为;(2)、当点 为劣弧 的中点,且 ∽ 时,求 的度数;(3)、当 ,且 为直角三角形时,求四边形 的面积(直接写出结果).26. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.
(1)、当 时, 的长度为;(2)、当点 为劣弧 的中点,且 ∽ 时,求 的度数;(3)、当 ,且 为直角三角形时,求四边形 的面积(直接写出结果).26. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.销售单价 (元)
3.5
5.5
销售量 (袋)
280
120
(1)、请直接写出y与x之间的函数关系式;(2)、如果每天获得160元的利润,销售单价为多少元?(3)、设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?27. 四边形ABCD是菱形,∠B≤90°,点E为边BC上一点,联结AE,过点E作EF⊥AE,EF与边CD交于点F,且EC=3CF.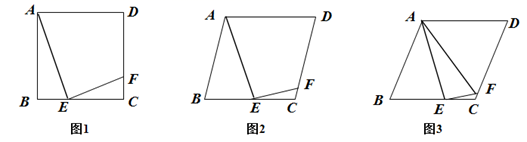 (1)、如图1,当∠B=90°时,求 与 的比值;(2)、如图2,当点E是边BC的中点时,求 的值;(3)、如图3,联结AF,当∠AFE=∠B且CF=2时,求菱形的边长.28. 如图,在平面直角坐标系中,直线 与 轴相交于点 ,与 轴相交于点 ,抛物线 经过 、 两点.
(1)、如图1,当∠B=90°时,求 与 的比值;(2)、如图2,当点E是边BC的中点时,求 的值;(3)、如图3,联结AF,当∠AFE=∠B且CF=2时,求菱形的边长.28. 如图,在平面直角坐标系中,直线 与 轴相交于点 ,与 轴相交于点 ,抛物线 经过 、 两点. (1)、求这条抛物线的解析式;(2)、设抛物线与 轴的另一个交点为 ,点 是抛物线上一点,点 是直线 上的一点,当四边形 是平行四边形时,求点 的坐标;(3)、在(2)的条件下,连接 ,在 的内部作射线 与抛物线的对称轴相交于点 ,且使得 ,请你直接写出线段 的长度.
(1)、求这条抛物线的解析式;(2)、设抛物线与 轴的另一个交点为 ,点 是抛物线上一点,点 是直线 上的一点,当四边形 是平行四边形时,求点 的坐标;(3)、在(2)的条件下,连接 ,在 的内部作射线 与抛物线的对称轴相交于点 ,且使得 ,请你直接写出线段 的长度.