宁夏石嘴山市平罗县2021年数学中考一模试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )A、 B、 C、 D、3. 不透明的袋子中装有两个小球,上面分别写着“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )A、 B、 C、 D、4. 某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是( )
 A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多455. 如图,直线 ,∠2+∠3=210°,则∠1=( )
A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多455. 如图,直线 ,∠2+∠3=210°,则∠1=( )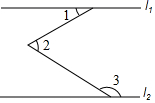 A、30° B、35° C、40° D、45°6. 实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是( )
A、30° B、35° C、40° D、45°6. 实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是( )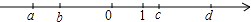 A、|a|>|b| B、|ac|=ac C、b<d D、c+d>07. 如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )
A、|a|>|b| B、|ac|=ac C、b<d D、c+d>07. 如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )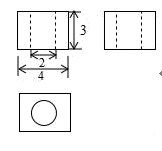 A、 B、 C、 D、8. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A、 B、 C、 D、8. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )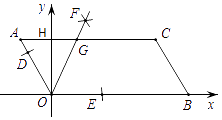 A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)
A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)二、填空题
-
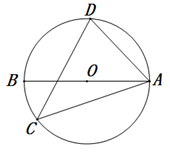
9. 在实数范围内分解因式: .10. 如图, 为 的直径, 为 的弦, ,则 的度数为.
 11. 若从-2,0,1这三个数中任取两个数,其中一个记为a,另一个记为b,则点A(a, b)恰好落在x轴上的概率是。12. 抛物线 ( 为常数)与x轴交点的个数是 .13. 如图,点A在反比例函数y= (x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 = ,△AOB的面积为6,则k的值为.
11. 若从-2,0,1这三个数中任取两个数,其中一个记为a,另一个记为b,则点A(a, b)恰好落在x轴上的概率是。12. 抛物线 ( 为常数)与x轴交点的个数是 .13. 如图,点A在反比例函数y= (x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 = ,△AOB的面积为6,则k的值为.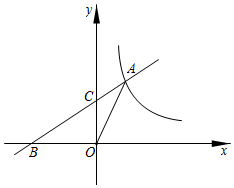 14. 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AC=2,则图中阴影部分的面积为(结果不取近似值).
14. 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AC=2,则图中阴影部分的面积为(结果不取近似值).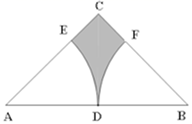 15. 如图,矩形 中, , ,点P在对角线 上,且 ,连接 并延长,交 的延长线于点Q,连接 ,则 的长为 .
15. 如图,矩形 中, , ,点P在对角线 上,且 ,连接 并延长,交 的延长线于点Q,连接 ,则 的长为 .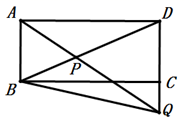 16. 《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案: .
16. 《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案: .三、解答题
-
17. 解不等式组 ,并把解集在数轴上表示出来18.(1)、先化简,再求值: ,其中 .(2)、解不等式组 ,并把它的解集在数轴上表示出来.
 19. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 , , .
19. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 , , .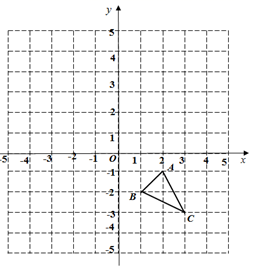 (1)、将 绕点 顺时针旋转 得到 ,请画出 ,并求出点 经过的路径长;(2)、以 为位似中心,将 放大2倍得到 ,请直接写出 的坐标.20. 某物流公司在疫情期间,要将300吨防疫物资运往某地,现有A、B两种型号的汽车可供调用.已知A型汽车每辆比B型车可多装5吨.6辆A型车与2辆B型车刚好能装完150吨物资.要求在每辆车不超载的条件下,把300吨防疫物资装运完.(1)、求A型车、B型车各能装多少吨物资?(2)、若确定调用5辆A型车,则至少还需调用B型车多少辆?21. 如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
(1)、将 绕点 顺时针旋转 得到 ,请画出 ,并求出点 经过的路径长;(2)、以 为位似中心,将 放大2倍得到 ,请直接写出 的坐标.20. 某物流公司在疫情期间,要将300吨防疫物资运往某地,现有A、B两种型号的汽车可供调用.已知A型汽车每辆比B型车可多装5吨.6辆A型车与2辆B型车刚好能装完150吨物资.要求在每辆车不超载的条件下,把300吨防疫物资装运完.(1)、求A型车、B型车各能装多少吨物资?(2)、若确定调用5辆A型车,则至少还需调用B型车多少辆?21. 如图,在菱形ABCD中,点E,F分别是边AD,AB的中点. (1)、求证:△ABE≌△ADF;(2)、若BE= ,∠C=60°,求菱形ABCD的面积.22. 2020年6月26日是第33个国际禁毒日,为了解同学们对禁毒知识的掌握情况,从广安市某校800名学生中随机抽取部分学生进行调查,调查分为“不了解”“了解较少”“比较了解”“非常了解”四类,并根据调查结果绘制出如图所示的两幅不完整的统计图.请根据统计图回答下列问题:
(1)、求证:△ABE≌△ADF;(2)、若BE= ,∠C=60°,求菱形ABCD的面积.22. 2020年6月26日是第33个国际禁毒日,为了解同学们对禁毒知识的掌握情况,从广安市某校800名学生中随机抽取部分学生进行调查,调查分为“不了解”“了解较少”“比较了解”“非常了解”四类,并根据调查结果绘制出如图所示的两幅不完整的统计图.请根据统计图回答下列问题: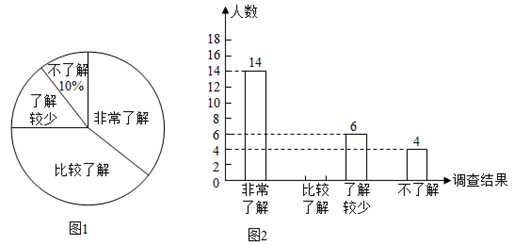 (1)、本次抽取调查的学生共有人,估计该校800名学生中“比较了解”的学生有人.(2)、请补全条形统计图.(3)、“不了解”的4人中有3名男生A1 , A2 , A3 , 1名女生B,为了提高学生对禁毒知识的了解,对这4人进行了培训,然后随机抽取2人叹才禁毒知识的掌握情况进行检测,请用画树状图或列表的方法,求恰好抽到2名男生的概率.23. 如图,△ABC中,∠ACB=90°,BO为△ABC的角平分线,以点O为圆心,OC为半径作⊙O与线段AC交于点D.
(1)、本次抽取调查的学生共有人,估计该校800名学生中“比较了解”的学生有人.(2)、请补全条形统计图.(3)、“不了解”的4人中有3名男生A1 , A2 , A3 , 1名女生B,为了提高学生对禁毒知识的了解,对这4人进行了培训,然后随机抽取2人叹才禁毒知识的掌握情况进行检测,请用画树状图或列表的方法,求恰好抽到2名男生的概率.23. 如图,△ABC中,∠ACB=90°,BO为△ABC的角平分线,以点O为圆心,OC为半径作⊙O与线段AC交于点D.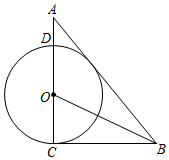 (1)、求证:AB为⊙O的切线;(2)、若tanA= ,AD=2,求BO的长.24. 为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
(1)、求证:AB为⊙O的切线;(2)、若tanA= ,AD=2,求BO的长.24. 为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.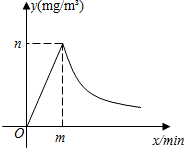 (1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.25. 通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的,下面是一个案例,请补充完整.
(1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.25. 通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的,下面是一个案例,请补充完整.原题;如图①,点 分别在正方形 的边 上, ,连接 ,则 ,试说明理由,
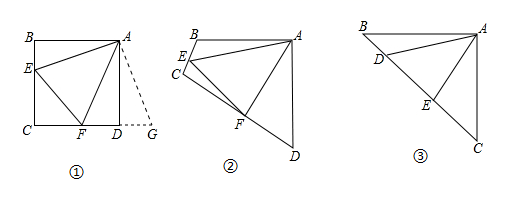 (1)、(思路梳理)
(1)、(思路梳理)∵ ,∴把 绕点A逆时针旋转 至 ,可使 与 重合,∵ ,∴ ,即:点 共线,根据“ ”,易证 , 得 ;
(2)、(类比引申)如图②,四边形 中, ,点 分别在 上, ,若 都不是直角,则当 与 满足等量关系时,仍有 ;
(3)、(联想拓展)如图③,在 中, ,点 均在边 上,且 ,猜想 应满足的等量关系,并写出推理过程.
26. 如图,平面直角坐标系中,四边形 为矩形,点 、 的坐标为 , .动点 、 分别从 、 同时出发,都以每秒1个单位的速度运动,其中,点 沿 向终点 运动,点 沿 向终点 运动,过点 作 ,交 于点 ,连接 ,已知动点运动了 秒.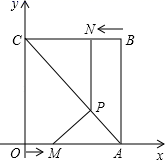 (1)、用含 的代数式表示 的坐标(直接写出答案);(2)、设 ,求 的最小值,并求此时 的值;(3)、是否存在 的值,使以 、 、 为顶点的三角形与 相似?若存在,请求出 的值;若不存在,请说明理由.
(1)、用含 的代数式表示 的坐标(直接写出答案);(2)、设 ,求 的最小值,并求此时 的值;(3)、是否存在 的值,使以 、 、 为顶点的三角形与 相似?若存在,请求出 的值;若不存在,请说明理由.