广西梧州市2021年九年级下学期数学抽样调研测试试卷
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、-2 B、2 C、 D、2. 下列图形中,不能通过其中一个阴影图形平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,直线 、 被直线 所截,下列条件能判断 的是( )
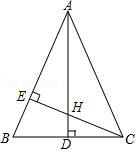
3. 如图,直线 、 被直线 所截,下列条件能判断 的是( ) A、 B、 C、 D、4. 梧州市脱贫攻坚取得了决定性进展,2015年至2019年全市累计脱贫247100人,数据247100用科学记数法表示为( )A、 B、 C、 D、5. 在2,8,4,3,2这组数据中,众数和中位数分别是( )A、2,4 B、2,3 C、3,2 D、4,26. 某校兴趣小组为了测量教学大楼的高度,用1.5m的竹竿作为测量工具.在阳光明媚的某天,该兴趣小组移动竹竿,使得竹竿顶端的影子与楼顶的影子在地面 处重合,如图,测得 , ,则教学楼 的高是( )
A、 B、 C、 D、4. 梧州市脱贫攻坚取得了决定性进展,2015年至2019年全市累计脱贫247100人,数据247100用科学记数法表示为( )A、 B、 C、 D、5. 在2,8,4,3,2这组数据中,众数和中位数分别是( )A、2,4 B、2,3 C、3,2 D、4,26. 某校兴趣小组为了测量教学大楼的高度,用1.5m的竹竿作为测量工具.在阳光明媚的某天,该兴趣小组移动竹竿,使得竹竿顶端的影子与楼顶的影子在地面 处重合,如图,测得 , ,则教学楼 的高是( ) A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 二次函数 的图象的顶点坐标是 ,且图象与 轴交于点 .将二次函数 的图象以原点为旋转中心顺时针旋转180°,则旋转后得到的函数解析式为( )A、 B、 C、 D、9. 如图,阴影部分①、②、③的面积分别记为 、 、 ,则 的面积与扇形 的面积之差等于( )
A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 二次函数 的图象的顶点坐标是 ,且图象与 轴交于点 .将二次函数 的图象以原点为旋转中心顺时针旋转180°,则旋转后得到的函数解析式为( )A、 B、 C、 D、9. 如图,阴影部分①、②、③的面积分别记为 、 、 ,则 的面积与扇形 的面积之差等于( ) A、 B、 C、 D、10. 如图,平行四边形 的周长是 ,对角线 于点,若 ,则 的长等于( )
A、 B、 C、 D、10. 如图,平行四边形 的周长是 ,对角线 于点,若 ,则 的长等于( ) A、 B、 C、 D、11. 如图, 是以 为直径的 上的一点, 是 的切线, , 为 的中点,连接 并延长交 于点 ,若 ,则 的长度为( )
A、 B、 C、 D、11. 如图, 是以 为直径的 上的一点, 是 的切线, , 为 的中点,连接 并延长交 于点 ,若 ,则 的长度为( ) A、 B、 C、 D、212. 已知 、 是关于 的一元二次方程 的两个根,且满足 , ,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、212. 已知 、 是关于 的一元二次方程 的两个根,且满足 , ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 计算:= .14. 分解因式:2x2+4x+2= .
15. 将浓度为30%的酒精与浓度为60%的酒精混合,制成了浓度为50%的酒精30kg.设浓度为30%的酒精需要 ,浓度为60%的酒精需要 ,则列出的方程组为.16. 如图, 是 的直径,点 、 在 上,弧 的度数是90°, , ,则 的直径 长为.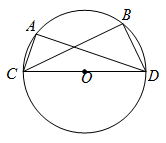 17. 如图,已知在四边形 中, .连接 ,若 , , , ,则点 到 的距离约为.(参考数据: , , .结果保留一位小数)
17. 如图,已知在四边形 中, .连接 ,若 , , , ,则点 到 的距离约为.(参考数据: , , .结果保留一位小数)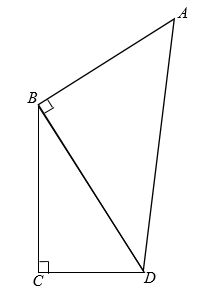 18. 如图,将矩形 沿EF折叠,使点B落在点 上,点 落在点 处.点 是折痕 上的任一点,过点 作 于点 , 交 于点 .若 , , ,则 的值是.
18. 如图,将矩形 沿EF折叠,使点B落在点 上,点 落在点 处.点 是折痕 上的任一点,过点 作 于点 , 交 于点 .若 , , ,则 的值是.
三、解答题
-
19. 计算:20. 解分式方程: .21. 如图,在四边形 中, 、 、 、 分别是 、 、 、 的中点,且 .

求证:四边形 是矩形.
22. 先化简后求值: ,其中 .23. 为了提高学生的身体素质,某校决定开展足球、排球、篮球、羽毛球四类课外体育运动项目,并要求每个学生仅参加其中的一类.为了了解学生对这四类体育运动项目的喜爱程度,学校做了一次抽样调查,并绘制了以下两幅不完整的统计图:
请根据图中信息回答下列问题:
(1)、此次调查一共抽取了多少名学生?请把条形统计图补充完整;(2)、在扇形统计图中,排球的百分比是多少?足球的圆心角是多少度?(3)、篮球项目现计划每20名学生配备一个篮球,如果该校有2400名学生,请你估计学校需要购买多少个篮球?24. 某超市经过记录发现近期龙眼的日销售量 (kg)与售价 (元/kg)有下表关系:10
12
15
20
196
176.4
147
98
(1)、请直接回答以上数据符合一次函数、反比例函数或二次函数中的哪一种?并求出 与 之间的函数解析式;(2)、已知龙眼的进货价是8元/kg,售价不能超过进货价的2倍,经调查平均每100kg龙眼会有2kg损耗,如果希望龙眼的每日利润是1005元,那么龙眼的售价应该定为多少元/kg?