广西贵港市桂平市2021年数学中考一模试卷

试卷更新日期：2021-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{1}{2}$ 的倒数是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 将210000用科学记数法表示为（）

A、 $21 \times 10^{4}$ B、 $2.1 \times 10^{5}$ C、 $2.1 \times 10^{6}$ D、21万

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 $8 x^{4} \div 2 x^{2} = 4 x^{2}$ D、 ${(- 2 a)}^{3} = 8 a^{3}$

查看试题解析
4. 一组数据：3，4，5，x，8 的众数是 5，则这组数据的方差是（）

A、2 B、2.4 C、2.8 D、3

查看试题解析
5. 在平面直角坐标系中，点 $P (- 3, m^{2} + 1)$ 关于原点对称点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 若 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两根，则 $x_{1} + x_{2} + x_{1} x_{2}$ 的值是（）

A、﹣1 B、1 C、5 D、﹣5

查看试题解析
7. 下列命题中，是假命题的是（）

A、两点之间，线段最短 B、 $3 a^{3} b$ 的系数是3 C、位似图形必定相似 D、若 $| a | = | b |$ ，则 $a = b$

查看试题解析
8. 关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x - 1}{2} - \frac{x + 2}{3} \leq 1 \\ x - a > 2 \end{array}$ 只有3个整数解，求 $a$ 的取值范围（）

A、 $8 \leq a < 9$ B、 $8 < a \leq 9$ C、 $8 < a < 9$ D、 $8 \leq a \leq 9$

查看试题解析
9. 如图，AB为⊙O的直径，点C在⊙O上，且CO⊥AB于点O，弦CD与AB相交于点E，若∠BEC= 68°，则∠ABD的度数为（）

A、20° B、23° C、25° D、34°

查看试题解析
10. 将抛物线y=﹣2x²+1向右平移1个单位，再向下平移3个单位后所得到的抛物线为（）

A、y=-2（x+1）²-2 B、y=-2（x+1）²-4 C、y=-2（x-1）²-2 D、y=-2（x-1）²-4

查看试题解析
11. 如图，在 $△ A B C$ 中，点 $E$ 是线段 $A C$ 上一点， $A E ∶ C E = 1 ∶ 2$ ，过点 $C$ 作 $C D ∥ A B$ 交 $B E$ 的延长线于点 $D$ ，若 $△ A B E$ 的面积等于4，则 $△ B C D$ 的面积等于（）

A、8 B、16 C、24 D、32

查看试题解析
12. 如图，在平行四边形 $A B C D$ 中， $A B = 2 A D$ ， $F$ 是 $C D$ 的中点，作 $B E ⊥ A D$ 于点 $E$ ，连接 $E F$ 、 $B F$ ，则下列结论错误的是（）

A、 $∠ C B F = ∠ A B F$ B、 $F E = F B$ C、 $2 S_{△ E F B} = S_{四边形 D E B C}$ D、 $∠ B F E = 3 ∠ D E F$

查看试题解析

二、填空题

13. 若分式 $\frac{x + 3}{x - 1}$ 的值为0，则x的值为.

查看试题解析
14. 计算 $\sqrt{{(- 4)}^{2}}$ 的结果是.

查看试题解析
15.
如图，∠1=∠2=40°，MN平分∠EMB ，则∠3=°．

查看试题解析
16. 如果在五张完全相同的卡片背后分别写上平行四边形、矩形、菱形、等边三角形、圆，打乱后随机抽取其中一张，那么抽取的图形既是轴对称图形又是中心对称图形的概率等于.

查看试题解析
17. 如图，正方形ABCD中，AB=2，将线段CD绕点C顺时针旋转90°得到线段CE，线段BD绕点B顺时针旋转90°得到线段BF，连接EF，则图中阴影部分的面积是.

查看试题解析
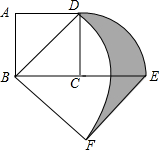18. 二次函数y=ax²+bx+c（a＜0）的图象与x轴的两个交点A、B的横坐标分别为﹣3、1，与y轴交于点C，下面四个结论：①16a+4b+c＜0；②若P（﹣5，y₁），Q（ $\frac{5}{2}$ ，y₂）是函数图象上的两点，则y₁＞y₂；③c=﹣3a；④若△ABC是等腰三角形，则b=﹣ $\frac{2 \sqrt{7}}{3}$ 或﹣ $\frac{2 \sqrt{15}}{3}$ ．其中正确的有．（请将正确结论的序号全部填在横线上）

查看试题解析

三、解答题

19.

(1)、计算： $| \sqrt{3} - 1 | + {(2021 - 1)}^{0} - {(- \frac{1}{3})}^{- 1} - 3 \tan 30 °$ .

(2)、解方程： $2 (x - 3) - (x + 3) (x - 3) = 0$ .

查看试题解析
20. 如图，在 $△ A B C$ 中，请用尺规作图法，在 $A B$ 边上找一点 $D$ ，使 $△ A C D ∽ △ A B C$ .（保留作图痕迹，不写作法）

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中，已知矩形 $O A B C$ 的顶点 $O$ 与坐标原点重合，顶点 $A$ ， $C$ 分别在坐标轴上，顶点 $B$ 的坐标为 $(4 ， 2)$ ，反比例函数 $y = \frac{k}{x}$ $(x > 0)$ 的图象与 $A B$ ， $B C$ 交于点 $M$ ， $N$ ，直线 $M N$ 与坐标轴交于 $D (0 ， 3)$ 和 $E (6 ， 0)$ 两点.

(1)、求直线 $M N$ 的函数表达式和 $k$ 的值；

(2)、求 $△ B M N$ 的面积.

查看试题解析

22. 中央电视台的“朗读者”节目激发了同学们的读书热情，为了引导学生“多读书，读好书”，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本书最少的有5本，最多的有8本，并根据调查结果绘制了不完整的图表，如图所示：

本数（本）	频数（人数）	频率
5	$a$	0.2
6	18	0.36
7	14	$b$
8	8	0.16
合计	$c$	1

(1)、统计表中的a= ， b= ， c=；

(2)、请将频数分布表直方图补充完整；

(3)、求所有被调查学生课外阅读的平均本数；

(4)、若该校八年级共有1200名学生，请你分析该校八年级学生课外阅读7本及以上的人数.

查看试题解析

23. 城镇老旧小区改造是重大民生工程和发展工程；安定区积极响应党的号召，全面推进城区老旧小区改造工作.现计划对城区某小区的居民自来水管道进行改造；该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的 $1.5$ 倍.如果由甲、乙队先合做 $15$ 天，那么余下的工程由甲队单独完成还需 $5$ 天.

(1)、这项工程的规定时间是多少天？

(2)、已知甲队每天的施工费用为 $3500$ 元，乙队每天的施工费用为 $2500$ 元.为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙两队合做来完成.则该工程施工费用是多少？

查看试题解析
24. 如图，点 $P$ 为正方形 $A B C D$ 的对角线 $A C$ 上的一点，连接 $B P$ 并延长交 $C D$ 于点 $E$ ，交 $A D$ 的延长线于点 $F$ ， $⊙ O$ 是 $△ D E F$ 的外接圆，连接 $D P$ .

(1)、求证： $D P$ 是 $⊙ O$ 的切线；

(2)、若 $\tan ∠ P D C = \frac{1}{2}$ ， $A B = 4$ ，求半径 $O E$ 的长.

查看试题解析
25. 如图，二次函数 $y = x^{2} + b x + c$ 的图象交 $x$ 轴于点 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ，交 $y$ 轴于点 $C$ .点 $P (m ， 0)$ 是 $x$ 轴上的一动点， $P M ⊥ x$ 轴，交直线 $A C$ 于点 $M$ ，交抛物线于点 $N$ .

(1)、求这个二次函数的表达式；

(2)、若点 $P$ 仅在线段 $A O$ 上运动，如图，求线段 $M N$ 长度的最大值.

查看试题解析
26. 已知 $△ A B C$ 是等边三角形， $A B = 6$ ，将一块含有30°角的直角三角板 $D E F$ 如图所示放置，让等边 $△ A B C$ 向右平移（ $B C$ 只能在 $E F$ 上移动）.如图1，当点 $E$ 与点 $B$ 重合时，点 $A$ 恰好落在三角板 $D E F$ 的斜边 $D F$ 上.

(1)、若点 $C$ 平移到与点 $F$ 重合，求等边 $△ A B C$ 平移的距离；

(2)、在等边 $△ A B C$ 向右平移的过程中， $A B$ ， $A C$ 与三角板斜边的交点分别为 $G$ ， $H$ ，连接 $E H$ 交 $A B$ 于点 $P$ ，如图2
①求证： $E B = A H$ ；

②若 $∠ H E F = 30 °$ ，求 $E H$ 的长；

③判断 $P G$ 的长度在等边 $△ A B C$ 平移的过程中是否会发生变化？如果不变，请求出 $P G$ 的长；如果变化，请说明理由.

查看试题解析