甘肃省白银市2021年九年级数学毕业会考综合试卷(一模)
试卷更新日期:2021-06-08 类型:中考模拟
一、单选题
-
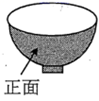
1. 如图,这是一个带“矮”圆柱形底的半球形的碗,则该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在 中,无理数的个数是( )A、2 B、3 C、4 D、53. 下列计算正确的是( )A、 B、 C、 D、4. 已知A、B两点的坐标分别是 和 ,下列结论错误的是( )A、点A在第二象限 B、点B在第一象限 C、线段 平行于y轴 D、点A、B之间的距离为45. 已知关于x的一元二次方程 ,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关6. 如图是小明和小华射击成绩的统计图,两人都射击了10次,下列说法正确的是( )
2. 在 中,无理数的个数是( )A、2 B、3 C、4 D、53. 下列计算正确的是( )A、 B、 C、 D、4. 已知A、B两点的坐标分别是 和 ,下列结论错误的是( )A、点A在第二象限 B、点B在第一象限 C、线段 平行于y轴 D、点A、B之间的距离为45. 已知关于x的一元二次方程 ,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关6. 如图是小明和小华射击成绩的统计图,两人都射击了10次,下列说法正确的是( )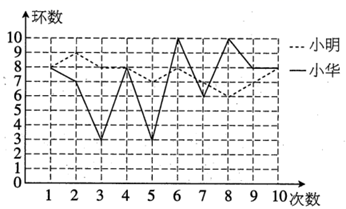 A、小明成绩的方差比小华成绩的方差大 B、小明和小华成绩的众数相同 C、小明成绩的中位数比小华成绩的中位数大 D、小明和小华的平均成绩相同7. 如图,在 中, 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )
A、小明成绩的方差比小华成绩的方差大 B、小明和小华成绩的众数相同 C、小明成绩的中位数比小华成绩的中位数大 D、小明和小华的平均成绩相同7. 如图,在 中, 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )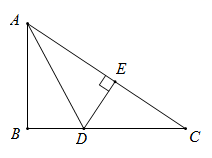 A、 B、1 C、2 D、68. 如图,平行四边形 中,点E为 边中点,连接 、 交于点F,若 的面积为2,则 的面积为( )
A、 B、1 C、2 D、68. 如图,平行四边形 中,点E为 边中点,连接 、 交于点F,若 的面积为2,则 的面积为( )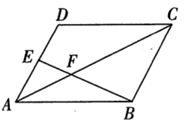 A、1 B、2 C、4 D、89. 如图, 是 的直径,点A,C在 上, 交 于点G.若 ,则 的度数为( )
A、1 B、2 C、4 D、89. 如图, 是 的直径,点A,C在 上, 交 于点G.若 ,则 的度数为( )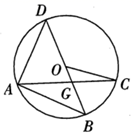 A、 B、 C、 D、10. 已知二次函数 经过点 和点 ,交x轴于A,B两点,交y轴于点C.① ;②该二次函数图象与y轴交于负半轴;③存在这样一个a,使得M、A、C三点在同一条直线上;④若 ,则 .以上说法正确的有( )A、①②③ B、①②④ C、①③④ D、②③④
A、 B、 C、 D、10. 已知二次函数 经过点 和点 ,交x轴于A,B两点,交y轴于点C.① ;②该二次函数图象与y轴交于负半轴;③存在这样一个a,使得M、A、C三点在同一条直线上;④若 ,则 .以上说法正确的有( )A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
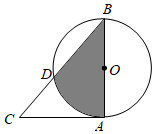
11. 已知 为三角形的三边,则b+a+c2a12. 据甘肃省统计局数据显示,2021年1~2月全省工业用电量167.1亿千瓦时,同比增长65%,167.1亿用科学记数法表示为.13. 分解因式: .14. 计算: .15. 如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 cm,则图中阴影部分的面积为 .
 16. 如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知 ,则点A的坐标为.
16. 如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知 ,则点A的坐标为.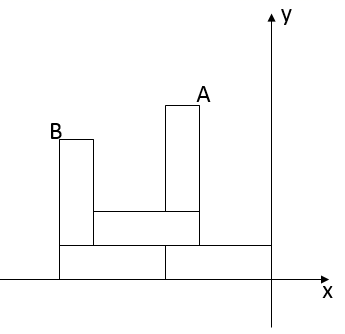 17. 如图,在 中, ,将 绕点A逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度为.
17. 如图,在 中, ,将 绕点A逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度为.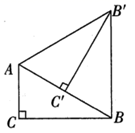 18. 在公园内,牡丹按正方形种植,在它的周围种植芍药,下图反映了牡丹的列数(n)和芍药的数量规律,那么当 时,芍药的数量为株.
18. 在公园内,牡丹按正方形种植,在它的周围种植芍药,下图反映了牡丹的列数(n)和芍药的数量规律,那么当 时,芍药的数量为株.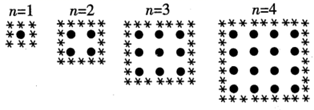
三、解答题
-
19. 计算: .20. 如图,B,C分别为射线 的端点,连接 ,按要求完成下列各小题.(保留作图痕迹,不要求写作法,标明各顶点字母)
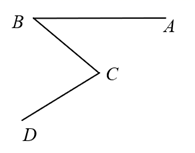
( 1 )在 的右侧,作 ,交射线 于点E;
( 2 )在(1)的条件下,求作 (点F在 内)使得 .
21. 读诗词解题:(通过列方程式,算出周瑜去世时的年龄)大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
22. 古代为了保护家园,在城池的四周修建护城河,为了方便交通,在护城河上安装了吊桥如图①所示,图②是图①的平面图,其中 为城墙, 为桥, 为吊绳,当收紧吊绳时,桥 运动到 处,若 ,求此时 的长度.(结果保留小数点后一位)( , , , , , , )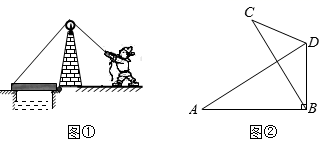 23. 甲、乙、丙、丁四个人玩“击鼓传花”的游戏,游戏规则:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.(1)、甲第一次传花时,恰好传给乙的概率是;(2)、求经过两次传花后,花恰好回到甲手中的概率.24. 为丰富学生的在校学习生活,激发学生的学习兴趣,提高对学科知识的深入理解,某校对本校学生进行了百科知识的测试,测试后随机抽取了部分学生的测试成绩,按“优秀、良好、及格、不及格”四个等级进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
23. 甲、乙、丙、丁四个人玩“击鼓传花”的游戏,游戏规则:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.(1)、甲第一次传花时,恰好传给乙的概率是;(2)、求经过两次传花后,花恰好回到甲手中的概率.24. 为丰富学生的在校学习生活,激发学生的学习兴趣,提高对学科知识的深入理解,某校对本校学生进行了百科知识的测试,测试后随机抽取了部分学生的测试成绩,按“优秀、良好、及格、不及格”四个等级进行统计分析,并将分析结果绘制成如下两幅不完整的统计图: (1)、求抽取的学生总人数;(2)、抽取的学生中,等级为“优秀”的人数为;扇形统计图中等级为“不及格”部分的圆心角的度数为;(3)、补全条形统计图;(4)、若该校有学生2500人,请根据以上统计结果估计成绩为“良好”及以上等级的学生共有多少人.25. 反比例函数y= (k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)、求抽取的学生总人数;(2)、抽取的学生中,等级为“优秀”的人数为;扇形统计图中等级为“不及格”部分的圆心角的度数为;(3)、补全条形统计图;(4)、若该校有学生2500人,请根据以上统计结果估计成绩为“良好”及以上等级的学生共有多少人.25. 反比例函数y= (k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.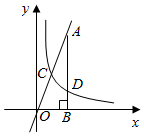 (1)、求k的值;(2)、在y轴上确定一点M,使点M到A,B两点距离之和d=MA+MB最小,求点M的坐标.26. 如图,在矩形 中, ,菱形 的三个顶点E,G,H分别在矩形 的边 上, ,连接 .
(1)、求k的值;(2)、在y轴上确定一点M,使点M到A,B两点距离之和d=MA+MB最小,求点M的坐标.26. 如图,在矩形 中, ,菱形 的三个顶点E,G,H分别在矩形 的边 上, ,连接 .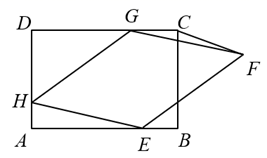 (1)、当 时,求证:四边形 是正方形.(2)、当 的面积为2时,求 的值.27. 如图,在⊙O中,弦AB与弦CD相交于G,OA⊥CD于点E,过B的直线与CD的延长线相交于点F,AC BF.
(1)、当 时,求证:四边形 是正方形.(2)、当 的面积为2时,求 的值.27. 如图,在⊙O中,弦AB与弦CD相交于G,OA⊥CD于点E,过B的直线与CD的延长线相交于点F,AC BF.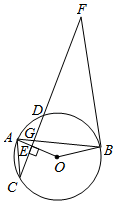 (1)、若 ,求证:BF是⊙O的切线;(2)、若tan∠F= ,CD=48,求⊙O的半径.28. 如图,直线 与 轴交于点 ,与 轴交于点 ,经过 、 两点的抛物线 与 轴的另一个交点为 .
(1)、若 ,求证:BF是⊙O的切线;(2)、若tan∠F= ,CD=48,求⊙O的半径.28. 如图,直线 与 轴交于点 ,与 轴交于点 ,经过 、 两点的抛物线 与 轴的另一个交点为 .

(备用图)
(1)、求抛物线的解析式;(2)、点 是直线 上方抛物线上的一个动点,过点 作 轴的平行线交直线 于点 ,当 面积最大时,求出点 的坐标;(3)、在(2)的结论下,连接AF,点 是抛物线对称轴上的动点,在抛物线上是否存在点 ,使得以 , , ,F为顶点的四边形是平行四边形?如果存在,请求出点 的坐标;如果不存在,请说明理由.