2015-2016学年陕西省咸阳市高一下学期期末数学试卷
试卷更新日期:2016-09-21 类型:期末考试
一、选择题
-
1. 下列各角中与﹣ 终边相同的是( )A、﹣ B、 C、 D、2. 某校高一(1)班共有40人,学号依次为1,2,3,…,40,现用系统抽样的方法抽取一个容量为5的样本,若学号为2,10,18,34的同学在样本中,则还有一个同学的学号应为( )A、27 B、26 C、25 D、243.
如图,两个变量具有相关关系的是( )
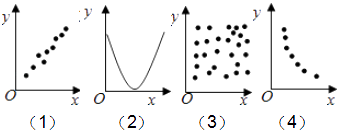 A、(1)(3) B、(1)(4) C、(2)(4) D、(2)(3)4. 已知某种彩票发行1000000张,中奖率为0.001,则下列说法正确的是( )A、买1张肯定不中奖 B、买1000张一定能中奖 C、买1000张也不一定能中奖 D、买1000张一定恰有1张能中奖5. 计算机执行如图所示的程序段后,输出的结果是( )
A、(1)(3) B、(1)(4) C、(2)(4) D、(2)(3)4. 已知某种彩票发行1000000张,中奖率为0.001,则下列说法正确的是( )A、买1张肯定不中奖 B、买1000张一定能中奖 C、买1000张也不一定能中奖 D、买1000张一定恰有1张能中奖5. 计算机执行如图所示的程序段后,输出的结果是( )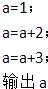 A、2 B、3 C、5 D、66. 如图所示的方格纸中有定点O,P,Q,A,B,C,D,则 + =( )
A、2 B、3 C、5 D、66. 如图所示的方格纸中有定点O,P,Q,A,B,C,D,则 + =( )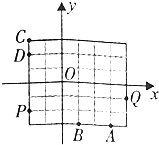 A、 B、 C、 D、7. 一个盒子内装有大小相同的红球、白球和黑球若干个,从中摸出1个球,若摸出红球的概率是0.45,摸出白球的概率是0.25,那么摸出黑球或白球的概率是( )A、0.3 B、0.55 C、0.75 D、0.78. 函数y=cos(2x﹣ )的图象的对称轴方程为( )A、x= + ,k∈Z B、x=kπ+ ,k∈Z C、x= + ,k∈Z D、x=kπ+ ,k∈Z9. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续的时间为50秒,若一行人来到该路口遇到红灯,则至少需要等待20秒才出现绿灯的概率为( )A、 B、 C、 D、10. 将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 个单位,得到的图象对应的解析式是( )A、y=sin(2x+ ) B、y=sin( x+ ) C、y=sin( x+ ) D、y=sin(2x+ )11. 已知变量x,y之间的线性回归方程为y=﹣x+13,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是( )
A、 B、 C、 D、7. 一个盒子内装有大小相同的红球、白球和黑球若干个,从中摸出1个球,若摸出红球的概率是0.45,摸出白球的概率是0.25,那么摸出黑球或白球的概率是( )A、0.3 B、0.55 C、0.75 D、0.78. 函数y=cos(2x﹣ )的图象的对称轴方程为( )A、x= + ,k∈Z B、x=kπ+ ,k∈Z C、x= + ,k∈Z D、x=kπ+ ,k∈Z9. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续的时间为50秒,若一行人来到该路口遇到红灯,则至少需要等待20秒才出现绿灯的概率为( )A、 B、 C、 D、10. 将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 个单位,得到的图象对应的解析式是( )A、y=sin(2x+ ) B、y=sin( x+ ) C、y=sin( x+ ) D、y=sin(2x+ )11. 已知变量x,y之间的线性回归方程为y=﹣x+13,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是( )x
6
8
10
12
y
6
m
3
2
A、可以预测,当x=9时,y=4 B、该回归直线必过点(9,4) C、m=4 D、m=512. 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< )的部分图象如图所示,则( )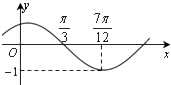 A、ω=2,φ= B、ω=2,φ= C、ω=1,φ= D、ω=1,φ=
A、ω=2,φ= B、ω=2,φ= C、ω=1,φ= D、ω=1,φ=二、填空题
-
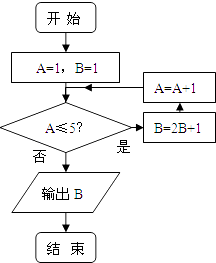
13. 设向量 =(m,﹣1), =(1,2),若 ,则m= .14. 已知一组数据按从小到大的顺序排列为:23,28,30,x,34,39,且其中位数是31,则x= .15. 若sin(π﹣α)= ,且α是锐角,则tan2α= .16. 若某程序框图如图所示,则该程序运行后输出的B等于 .
三、解答题
-
17. 已知sinα= ,α∈( ,π)(1)、tan(α+π)的值;(2)、cos(α﹣ )sin(α+ )的值.18. 已知如图所示的程序框图
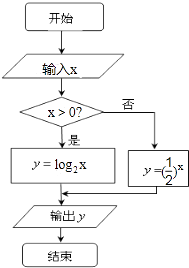 (1)、当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;(2)、当输出的结果为4时,求输入的x的值.19. 为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人
(1)、当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;(2)、当输出的结果为4时,求输入的x的值.19. 为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人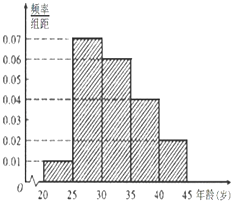 (1)、求该组织的人数;(2)、若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?20. 已知函数f(x)=sinx+ cosx.求:(1)、f(x)图象的对称中心的坐标;(2)、f(x)的单调区间.
(1)、求该组织的人数;(2)、若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?20. 已知函数f(x)=sinx+ cosx.求:(1)、f(x)图象的对称中心的坐标;(2)、f(x)的单调区间.