陕西省西安市八校2021届高三下学期文数第三次联考试卷
试卷更新日期:2021-06-08 类型:高考模拟
一、单选题
-
1. 已知集合A、集合 ,且 ,则下列结论正确的是( )A、有可能 B、 C、 D、2. 在复平面上,若点 、 对应的复数分别为 、 ,则 ( )A、1 B、 C、2 D、3. 不透明袋子里有大小完全相同的10只小球,其中4只蓝色6只红色,小朋友花花想从袋子里取到一只红色小球,第一次从袋子里随机取出一只小球,却是蓝色,不放回,再取第二次.则小朋友花花第二次取到红色小球的概率是( )A、 B、 C、 D、4. 一个空间几何体的三视图外轮廓均为边长是3的正方形,如图所示,则其表面积为( )
 A、 B、 C、 D、5. 已知 .则下面算法框图输出的结果是( )
A、 B、 C、 D、5. 已知 .则下面算法框图输出的结果是( ) A、47 B、48 C、49 D、506. 已知 ,则 ( )A、120 B、210 C、336 D、5047. 在 中,已知 , ,若 ,则 ( )A、 B、 C、 D、8. 已知椭圆: .则椭圆的离心率的取值范围为( )A、 B、 C、 D、9. 有下列命题: :幂函数 的定义域为实数集 ; :已知数据 , ,…, 的平均数为 ,方差 ,则 ; :若 函数的导函数为 , 的解为 ,则 为函数 的极值点; :变量 , 负相关,相关系数为 ,则 越大相关性越弱,越小相关性越强.则真命题为( )A、 B、 C、 D、10. 为了解某电子产品的使用寿命,从中随机抽取了100件产品进行测试,得到图示统计图.依据统计图,估计这100件产品使用寿命的平均值(用各组的中间值代替该组的平均值)为( )
A、47 B、48 C、49 D、506. 已知 ,则 ( )A、120 B、210 C、336 D、5047. 在 中,已知 , ,若 ,则 ( )A、 B、 C、 D、8. 已知椭圆: .则椭圆的离心率的取值范围为( )A、 B、 C、 D、9. 有下列命题: :幂函数 的定义域为实数集 ; :已知数据 , ,…, 的平均数为 ,方差 ,则 ; :若 函数的导函数为 , 的解为 ,则 为函数 的极值点; :变量 , 负相关,相关系数为 ,则 越大相关性越弱,越小相关性越强.则真命题为( )A、 B、 C、 D、10. 为了解某电子产品的使用寿命,从中随机抽取了100件产品进行测试,得到图示统计图.依据统计图,估计这100件产品使用寿命的平均值(用各组的中间值代替该组的平均值)为( )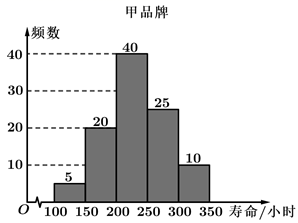 A、218.25 B、231.25 C、232.5 D、241.2511. 函数 的部分图像如图所示,则 在闭区间 上的最小值和最大值依次为( )
A、218.25 B、231.25 C、232.5 D、241.2511. 函数 的部分图像如图所示,则 在闭区间 上的最小值和最大值依次为( ) A、 ,2 B、 , C、 ,0 D、0,212. 已知函数 是增函数,且 恒成立,则 的取值范围为( )A、 B、 C、 D、
A、 ,2 B、 , C、 ,0 D、0,212. 已知函数 是增函数,且 恒成立,则 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 曲线 在点(e,f(e))处的切线方程为
14. 已知在 中, ,则 .15. 已知直线 与双曲线 的两条渐近线围成的三角形的面积为2,则双曲线C的焦距的最小值为.16. 现在有红豆、白豆各若干粒.甲乙两人为了计算豆子的粒数,选用了这样的方法:第一轮甲每次取4粒红豆,乙每次取2粒白豆,同时进行,当红豆取完时,白豆还剩10粒;第二轮,甲每次取1粒红豆,乙每次取2粒白豆,同时进行,当白豆取完时,红豆还剩 粒.则红豆和白豆共有粒.三、解答题
-
17. 已知数列 的前 项和为 ,且 ,当 时 .(1)、求数列 的通项公式;(2)、设 ,设 ,求数列 的前 项和为 .18. 某中学高一(1)班在接种了“新冠疫苗”之后,举行了“疫情防控,接种疫苗”知识竞赛.这次竞赛前21名同学成绩的茎叶图如图所示,已知前7名女生的平均得分为221分.(1)、求茎叶图中x的值;(2)、如果在竞赛成绩高于205分且按男生和女生分层抽样抽取6人,再从这6人中任选3人作为后期举行的“接种疫苗,感恩祖国”主题班会中心发言人,求这3人中有女生的概率.19. 已知圆 与抛物线 交于 、 两点( 在第一象限), .(1)、求抛物线 的方程;(2)、设过A点的两条直线 与 关于直线 对称,直线 与 与抛物线 都有两个不同交点,且另一交点分别为 、 ,求直线 的斜率.20. 在正六棱柱 中, , , 为侧棱 的中点, 为棱 上一点, 为下底面 的中心.
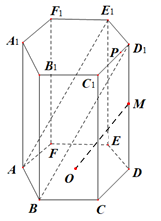 (1)、求证: 平面 ;(2)、求四棱锥 的体积.
(1)、求证: 平面 ;(2)、求四棱锥 的体积.