湖南省永州市省重点中学2021届高三下学期数学5月联考试卷
试卷更新日期:2021-06-07 类型:高考模拟
一、单选题
-
1. 已知 ,复数 的共轭复数 在复平面内对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知集合 ,集合 ,则 ( )A、 B、 C、 D、3. 若圆 被直线 截得的弦长为6,则 ( )A、26 B、31 C、39 D、434. 函数 的图象大致为( )A、
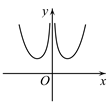 B、
B、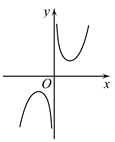 C、
C、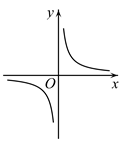 D、
D、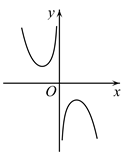 5. 三星堆古遗址是迄今在西南地区发现的范围最大,延续时间最长,文化内涵最丰富的古城、古国、古蜀文化遗址.三星堆遗址被称为20世纪人类最伟大的考古发现之一,昭示了长江流域与黄河流域一样,同属中华文明的母体,被誉为“长江文明之源”,考古学家在测定遗址年代的过程中,利用“生物死亡后体内的碳14含量按确定的比率衰减”这一规律,建立了样本中碳14的含量,随时间x(年)变化的数学模型: ( 表示碳14的初始量).2020年考古学家对三星堆古遗址某文物样本进行碳14年代学检测,检测出碳14的含量约为初始量的68%,据此推测三星堆古遗址存在的时期距今大约是( )(参考数据: )A、2796年 B、3152年 C、3952年 D、4480年6. 已知等差数列 的前 项和为 , ,则 ( )A、21 B、11 C、-21 D、07. 展开式中 的系数为( )A、-3 B、3 C、-15 D、158. 在三棱锥 中,底面 是面积为 的正三角形,若三棱锥 的每个顶点都在球 的球面上,且点 恰好在平面 内,则三棱锥 体积的最大值为( )A、 B、 C、 D、
5. 三星堆古遗址是迄今在西南地区发现的范围最大,延续时间最长,文化内涵最丰富的古城、古国、古蜀文化遗址.三星堆遗址被称为20世纪人类最伟大的考古发现之一,昭示了长江流域与黄河流域一样,同属中华文明的母体,被誉为“长江文明之源”,考古学家在测定遗址年代的过程中,利用“生物死亡后体内的碳14含量按确定的比率衰减”这一规律,建立了样本中碳14的含量,随时间x(年)变化的数学模型: ( 表示碳14的初始量).2020年考古学家对三星堆古遗址某文物样本进行碳14年代学检测,检测出碳14的含量约为初始量的68%,据此推测三星堆古遗址存在的时期距今大约是( )(参考数据: )A、2796年 B、3152年 C、3952年 D、4480年6. 已知等差数列 的前 项和为 , ,则 ( )A、21 B、11 C、-21 D、07. 展开式中 的系数为( )A、-3 B、3 C、-15 D、158. 在三棱锥 中,底面 是面积为 的正三角形,若三棱锥 的每个顶点都在球 的球面上,且点 恰好在平面 内,则三棱锥 体积的最大值为( )A、 B、 C、 D、二、多选题
-
9. 已知平面向量 ,且 ,则( )A、 B、 C、 D、10. 若关于 的方程 在区间 上有且只有一个解,则 的值可能为( )A、-2 B、-1 C、0 D、111. 已知 ,且 ,则( )A、 B、 C、 D、12. 设 同时为椭圆 与双曲线 的左右焦点,设椭圆 与双曲线 在第一象限内交于点 ,椭圆 与双曲线 的离心率分别为 为坐标原点,若( )A、 ,则 B、 ,则 C、 ,则 的取值范围是 D、 ,则 的取值范围是
三、填空题
-
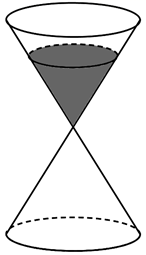
13. 若 ,则 .14. 沙漏是一种古代的计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时,如图,某沙漏由上、下两个圆锥组成,该圆锥的高为1,若上面的圆锥中装有高度为 的液体,且液体能流入下面的圆锥,则液体流下去后的液面高度为.
 15. 规定记号" "表示一种运算,即 ,若 ,函数 的图象关于直线 对称,则 .16. 三分损益法是古代中国发明制定音律时所用的生律法.三分损益包含“三分损一"“三分益一"两层含义,三分损一是指将原有长度作3等分而减去其1份,即原有长度 生得长度;而三分益一则是指将原有长度作3等分而增添其1份,即原有长度 生得长度,两种方法可以交替运用、连续运用,各音律就得以辗转相生,假设能发出第一个基准音的乐器的长度为243,每次损益的概率为 ,则经过5次三分损益得到的乐器的长度为128的概率为.
15. 规定记号" "表示一种运算,即 ,若 ,函数 的图象关于直线 对称,则 .16. 三分损益法是古代中国发明制定音律时所用的生律法.三分损益包含“三分损一"“三分益一"两层含义,三分损一是指将原有长度作3等分而减去其1份,即原有长度 生得长度;而三分益一则是指将原有长度作3等分而增添其1份,即原有长度 生得长度,两种方法可以交替运用、连续运用,各音律就得以辗转相生,假设能发出第一个基准音的乐器的长度为243,每次损益的概率为 ,则经过5次三分损益得到的乐器的长度为128的概率为.四、解答题
-
17. 在① 成等差数列;② ;③ 这三个条件中任选一个,补充在下面问题中.若问题中的三角形存在,求该三角形面积的值;若问题中的三角形不存在,说明理由.
问题:是否存在 ,它的内角 的对边分别为 ,且 , , ▲ ?
注:如果选择多个条件分别解答,按第一个解答计分.
18. 在公比大于0的等比数列 中,已知 依次组成公差为4的等差数列(1)、求 的通项公式;(2)、设 ,求数列 的前 项和19. 如图,在四棱锥 中, , , ,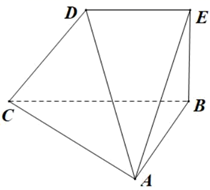 (1)、证明: .(2)、若平面 平面 ,经过 、 的平面 将四棱锥 分成左、右两部分的体积之比为 ,求平面 与平面 所成锐二面角的余弦值.20. 已知抛物线 的焦点为 ,点 在抛物线 上, .(1)、求抛物线 的标准方程.(2)、已知直线 交抛物线 于点 ,且 ,证明:直线 过定点.21. 某企业有甲、乙两条生产同种产品的生产线,据调查统计,100次生产该产品所用时间的频数分布表如下:假设订单A约定交货时间为11天,订单B约定交货时间为12天.(将频率视为概率,当天完成即可交货)
(1)、证明: .(2)、若平面 平面 ,经过 、 的平面 将四棱锥 分成左、右两部分的体积之比为 ,求平面 与平面 所成锐二面角的余弦值.20. 已知抛物线 的焦点为 ,点 在抛物线 上, .(1)、求抛物线 的标准方程.(2)、已知直线 交抛物线 于点 ,且 ,证明:直线 过定点.21. 某企业有甲、乙两条生产同种产品的生产线,据调查统计,100次生产该产品所用时间的频数分布表如下:假设订单A约定交货时间为11天,订单B约定交货时间为12天.(将频率视为概率,当天完成即可交货)所用的时间(单位:天)
10
11
12
13
甲生产线的频数
10
20
10
10
乙生产线的频数
5
20
20
5
(1)、为尽最大可能在约定时间交货,判断订单A和订单B应如何选择各自的生产线(订单A , B互不影响);(2)、已知甲、乙生产线的生产成本分别为3万元、2万元,订单A , B互不影响,若规定实际交货时间每超过一天就要付5000元的违约金,现订单A , B用(1)中所选的生产线生产产品,记订单A , B的总成本为 (万元),求随机变量 的期望值.22. 已知函数(1)、讨论 的单调性;(2)、当 时, 恒成立 ,求 的取值范围.