山东省聊城市冠县2021年中考数学一模试卷
试卷更新日期:2021-06-07 类型:中考模拟
一、单选题
-
1. 实数0、 、 、 中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 如图使用五个相同的立方体搭成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 是指大气中直径≤0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )A、 B、 C、 D、4. 函数y= 的自变量x的取值范围是( )A、x≥-1 B、x≥-1且x≠2 C、x≠±2 D、x>-1且x≠25. 分解因式 结果正确的是( )A、 B、 C、 D、6. 商店某天销售了14件衬衫,其领口尺寸统计如表:
3. 是指大气中直径≤0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )A、 B、 C、 D、4. 函数y= 的自变量x的取值范围是( )A、x≥-1 B、x≥-1且x≠2 C、x≠±2 D、x>-1且x≠25. 分解因式 结果正确的是( )A、 B、 C、 D、6. 商店某天销售了14件衬衫,其领口尺寸统计如表:领口尺寸(单位:cm)
38
39
40
41
42
件数
1
5
3
3
2
则这14件衬衫领口尺寸的众数与中位数分别是( )
A、39cm、39cm B、39cm、39.5cm C、39cm、40cm D、40cm、40cm7. 如图,直线 ,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( ) A、105° B、110° C、115° D、120°8. 关于x的不等式组 恰有四个整数解,那么m的取值范围为( )A、m≥﹣1 B、m<0 C、﹣1≤m<0 D、﹣1<m<09. 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB= ,则阴影部分的面积是( )
A、105° B、110° C、115° D、120°8. 关于x的不等式组 恰有四个整数解,那么m的取值范围为( )A、m≥﹣1 B、m<0 C、﹣1≤m<0 D、﹣1<m<09. 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB= ,则阴影部分的面积是( ) A、 B、 C、﹣ D、﹣10. 方程 有两个相等的实数根,且满足 则m的值是( )A、-2或3 B、3 C、-2 D、-3或211. 如图,在平面直角坐标系xOy中,直线
A、 B、 C、﹣ D、﹣10. 方程 有两个相等的实数根,且满足 则m的值是( )A、-2或3 B、3 C、-2 D、-3或211. 如图,在平面直角坐标系xOy中,直线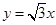 经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( )
经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( ) 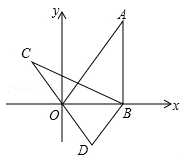 A、(﹣1, ) B、(﹣2, ) C、( ,1) D、( ,2)12. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A、(﹣1, ) B、(﹣2, ) C、( ,1) D、( ,2)12. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )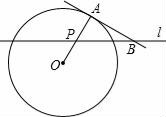 A、
A、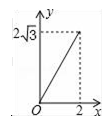 B、
B、 C、
C、 D、
D、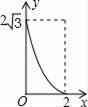
二、填空题
-
13. 若a、b互为相反数,c、d互为倒数,m的绝对值为2,则 .14. 三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为 cm.
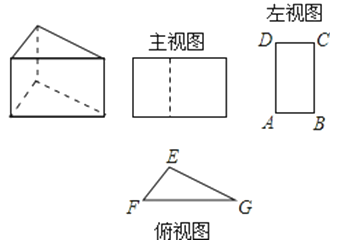 15. 如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面半径为 .
15. 如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面半径为 . 16.
16.如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是 .
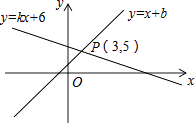 17. 如图,在平面内直角坐标系中,直线 交 轴于点 ,交 轴于点 点 , , ,…在 轴上,点 , , ,…在直线 上.若 , , ,…均为等边三角形,则 的长是 .
17. 如图,在平面内直角坐标系中,直线 交 轴于点 ,交 轴于点 点 , , ,…在 轴上,点 , , ,…在直线 上.若 , , ,…均为等边三角形,则 的长是 .
三、解答题
-
18. 计算:19. 为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩
频数
频率
优秀
45
b
良好
a
0.3
合格
105
0.35
不合格
60
c
 (1)、该校初三学生共有多少人?(2)、求表中a,b,c的值,并补全条形统计图.(3)、初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.20. 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)、该校初三学生共有多少人?(2)、求表中a,b,c的值,并补全条形统计图.(3)、初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.20. 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE. (1)、求证:△ADE≌△CED;(2)、求证:DE∥AC.21. 如图,某数学兴趣小组想测量一棵树 的高度,他们先在点 处测得树顶 的仰角为 ,然后沿 方向前行 ,到达 点,在 处测得树项 的仰角高度为 ( 、 、 三点在同一直线上).请你根据他们测量数据计算这棵树 的高度(结果精确到 ).(参考数据: , )
(1)、求证:△ADE≌△CED;(2)、求证:DE∥AC.21. 如图,某数学兴趣小组想测量一棵树 的高度,他们先在点 处测得树顶 的仰角为 ,然后沿 方向前行 ,到达 点,在 处测得树项 的仰角高度为 ( 、 、 三点在同一直线上).请你根据他们测量数据计算这棵树 的高度(结果精确到 ).(参考数据: , ) 22. 某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
22. 某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:甲
乙
进价(元/部)
4000
2500
售价(元/部)
4300
3000
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)、该商场计划购进甲、乙两种手机各多少部?(2)、通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.23. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数 (m≠0)的图象交于点A(3,1),且过点B(0,-2). (1)、求反比例函数和一次函数的表达式.(2)、如果点P是x轴上位于直线AB右侧的一点,且ΔABP的面积是3,求点P的坐标.
(1)、求反比例函数和一次函数的表达式.(2)、如果点P是x轴上位于直线AB右侧的一点,且ΔABP的面积是3,求点P的坐标.